Тема 3. Типовые динамические звенья

3.1 Преобразование Лапласа

Дифференциальное уравнение, описываемое взаимосвязь выходного и входного сигналов в динамическом режиме работы, называется динамической характеристикой.

Для получения математической модели достаточно использовать несколько типовых уравнений взаимосвязи выходного и входного сигналов элементов САУ, которые называются типовыми динамическими звеньями (ТДЗ).

Передаточной функцией (ПФ) называется преобразованное по Лапласу исходное дифференциальное уравнение, т.е. уравнение, записанное в виде отношения преобразованных по Лапласу выходного и входного сигналов звена.

В преобразовании по Лапласу исходное дифференциальное уравнение называется оригиналом, а преобразованное и записанное в операторной форме уравнение – его изображением. Суть преобразования Лапласа заключается в замене функций вещественных переменных х _вых(t) и х_вх (t) на функции комплексных переменных х _вых(s) и х_вх (s), где s – комплексное число s = ±σ ± jω. Эти функции связаны между собой интегралом Лапласа:

В сокращенной форме записи

x(s) = L{x(t)} или x(s) ≡ x(t),

где L – оператор Лапласа; x(s) – изображение; x(t) – оригинал.

Пьер Симон Лаплас (1749 - 1827) – французский математик, астроном, физик. Основоположник дифференциальных уравнений, теории вероятностей.

Обратное преобразование Лапласа

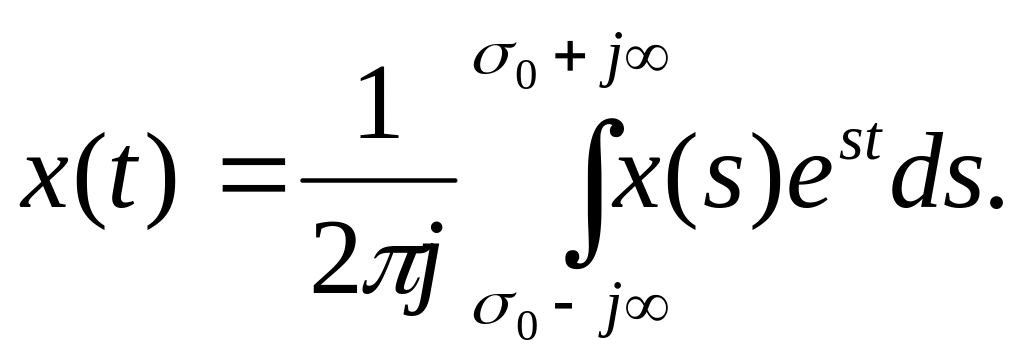
Этот интеграл берется вдоль любой прямой Re s = σ₀.

В сокращенной форме записи

x(t) = L^-1 {x(s)},

где L^-1 – обратный оператор Лапласа.

Основные свойства преобразований Лапласа:

1) линейности L{α x₁(t) + β x₂(t)} = α L{x₁(t)} + β L{x₂(t)};

2) дифференцирование при нулевых начальных условиях

3) интегрирование

4) теорема запаздывания

5) теорема о свертке или умножение изображений

6) теорема деления изображений

при m < n

где m и n – степень числителя и знаменателя.

а) если известно, что корни кратные, то

где s_k – корни знаменателя B(s) = 0; n_k – их кратность; l – число различных корней.

б) если все корни простые, то

где n – степень знаменателя B(s) = 0;

Формальным условием перехода от оригинала к изображению будут следующие замены: d/dt на s; d²/dt² на s² и т.д.

Таким образом, легко можно получить из оригинала изображение, т.е. операторную форму записи дифференциального уравнения ТДЗ.

3.2 Частотные и временные характеристики звеньев

Частотные характеристики звеньев (системы) получают путем подачи на вход гармонического сигнала с постоянной амплитудой и переменной частотой от нуля до ∞, при этом замеряя на выходе амплитуду и фазу сигнала.

Подставим в ПФ звена s = jω

где - модуль ПФ; - фаза ПФ или сдвиг фазы выходного сигнала.

Экспериментально для построения амплитудно-фазовой частотной характеристики или годографа требуются в генератор частоты, вольтметр и частотомер.

Для построения логарифмических амплитудно-частотных характеристик используется выражение

L(ω) = 20 lg A(ω).

По оси абсцисс откладываются частоты, выраженные в логарифмах lg ω, подекадно: 1, 10, 100…. или в логарифмах 0, 1, 2 …

Временная характеристика звена (системы) определяется переходной функцией h(t) или кривой разгона, описывающей реакцию звена (системы) на единичный входной сигнал 1(t)

Импульсной переходной или весовой функцией ω(t) звена (системы) называют функцию, описывающую реакцию на единичное импульсное воздействие или дельта функции при нулевых начальных условиях.

Импульсная переходная функция и переходная функция связаны выражением