1.5. Точки экстремума

Определение[3]. Точку называют точкой максимума функции , если у этой точки существует окрестность, для всех точек которой, кроме самой точки , выполняется неравенство .

Определение[3]. Точку называют точкой минимума функции , если у этой точки существует окрестность, для всех точек которой, кроме самой точки , выполняется неравенство .

Точками экстремума называют точки минимума и максимума.

Алгоритм исследования непрерывной функции на монотонность и нахождение точек экстремума.

1) Найти область определения функции ;

2) Найти производную

2) Найти критические точки (решить уравнение и определить точки, в которых производная не существует);

3) Отметить критические точки на числовой прямой и определить знаки производной на получившихся промежутках.

4) Сделать вывод о монотонности функции

5) Определить точки экстремума.

1.6. Преобразование графиков функции

1. для построения графика функции необходимо осуществить параллельный перенос графика функции на единиц вдоль оси вверх/вниз, если .

2. Для построения графика функции необходимо осуществить параллельный перенос графика функции на единиц вдоль оси вправо/влево , если .

3. Для построения графика функции необходимо отобразить график функции симметрично относительно оси .

4. Для построения графика функции необходимо отобразить график функции симметрично оси .

5. Для построения графика функции необходимо ту часть графика функции , которая находится ниже оси отобразить симметрично относительно этой оси.

6. для построения графика функции необходимо ту часть графика функции , которая находится правее оси отобразить симметрично этой оси.

7. Для построения графика функции при необходимо провести растяжения/ сжатие графика функции в раз вдоль оси .

8. Для построения графика функции при необходимо провести сжатие/ растяжение графика функции в раз вдоль оси .

Глава 2. Набор заданий

Во данной главе построены изображения с помощью элементарных функций. На основе полученных таким образом карточек составлен и прорешан приведен набор заданий по темам: функция, предел функции в точке, геометрический смысл производной функции в точке.

2.1. Построение изображения «логотип»

Использованы графики функций и и с помощью элементарных преобразований (параллельный перенос графика вдоль оси, симметричное отражения графика относительно оси ординат, симметричное отражение графика относительно оси абсцисс).

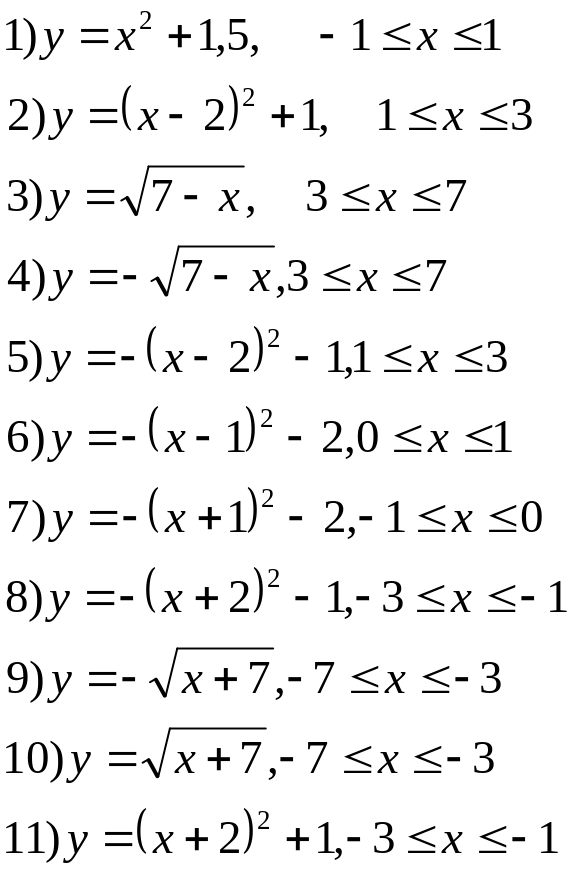
2.2. Задания на основе изображения

Задания для 6 класса:

1) Имеет ли место быть на данном изображении осевая симметрия?

2) Если да, то относительно, какой прямой?

3 ) Найдите координаты точек: используя рисунок.

Ответы: 1) имеет; 2) относительно оси ; 3) ; ; ;

Задания для 7 класса

1) найдите наибольшее и наименьшее значение функции на всем числовом промежутке

Решение: в 7 классе

2) даны функции:

,вычислить

Ответы: 1) ; . 2) ; ;

Задания для 8 класса

1) Найдите область определения функции

2) Найдите область значения функции

3) Найдите промежутки возрастания функции

Ответы: 1) . 2) . 3) функция возрастает на промежутке

Задания для 9 класса

1) выясните, куда выпукла функция на промежутке

Ответы: 1) . 2) функция выпукла вниз.

Задания для 10-11 класса:

1) Составьте уравнение касательной к графику функции в точке

2) Найдите точки экстремума функции

3) В каких точках производная функции будет равна ?

Ответы: 1) 1. вычисляем , . 2. вычисляем . 3. . 4. подставляем значения в формулу: , .

2) 1. ищем ; 2. , точка будет являться точкой экстремума функции .

3) в точке

1) найдите наибольшее и наименьшее значение функции на всем числовом промежутке

Решение: в 10-11 классах с помощью производной