
Розв'язання
а) Скористаємося ознакою Даламбера :
![]()
ряд рожбіжний.
б) Скористаємося ознакою Даламбера . Для данного ряду маємо
![]() ,
,
![]() ;
;
![]()
За
ознакою Даламбера ряд буде абсодютно
збіжним , якщо
![]() <1
, звідки
<1
, звідки
-1<x+3<1 , або -4<x<-2 . Таким чином , (-4;-2) – інтервал збіжності даного ряду і R=1 –
його радіус збіжності.
Дослідимо збіжнісь цього ряду на кінцях інтервалу збіжності.
При x=-4 маємо ряд
![]() ,
,
який є збіжним за ознакою Лейбніца.
При x=-2 дістанемо узагальнений гармонічний ряд
![]() ,
,
який
також збіжний
![]() . Отже , областю збіжності даного ряду
є відрізок
. Отже , областю збіжності даного ряду
є відрізок
[-4;-2].
Задача
9 Розкласти
в ряд Фур’є
![]() -періодичну
функцію
-періодичну
функцію
![]() .
.
Розв’язання
Задана
функція кусково-монотонна на проміжку
![]() ,
тому її можна зобразити рядом Фур’є
.
,
тому її можна зобразити рядом Фур’є
.
Маємо
![]() ;
;
![]()
![]() ;
;
![]()
![]()
![]() .
.
Підставивши
знайдені коефіцієнти в ряд
![]() ,
,
дістанемо
![]() .
.
Задача 10 Обчислити подвійний інтеграл , використувуючи полярні координати
![]() .
.
Розв’язання.
Покладемо
![]() і застосовуючи формулу
і застосовуючи формулу
![]() ,
,
маємо
![]() .
.
Рівняння
кола
![]() =2ax
в
полярніх координатах має вигляд
=2ax
в
полярніх координатах має вигляд
![]() .
.
Тому
областю
![]() є
область , обмежена знизу віссю r=0
,
зверху косинусоїдою
, де
є
область , обмежена знизу віссю r=0
,
зверху косинусоїдою
, де
![]() .
.
Отже ,

 .
.
Задача
11 Знайти
масу тіла , розміщеного в об’ємі
V
, якщо
![]() - густина ,
- густина ,
![]()
Розв’язання
Обчислення проведемо за допомогою формули
![]() .
.
Перейшовши до сферичних координат , маємо :
 .
.
Задача
12.
Обчислити
криволінейний інтеграл
![]()
де
L-коло:![]()
Розв’язання
Скористаємось параметричними рівняннями кола:
![]()
Тоді dx= -Rsin tdt, dy= Rcos tdt, тому
![]()
![]()
Такий самий результат дістанемо за формулою Гріна:
![]()
![]()
Задача
13 Обчислити
: 1) потік векторного поля
![]() через зовнишну поверхню піраміди ,
утвореної площиною (P):
x+2y+2z-1=0
і
координатами площинами;
через зовнишну поверхню піраміди ,
утвореної площиною (P):
x+2y+2z-1=0
і
координатами площинами;
2)ціркуляцію
векторного поля
по
контуру трикутника , отриманого в
результаті перетину площини (P):
x+2y+2z-1=0
з
координатними площинами , при додатному
напрямі обходу віднооно нормального
вектора
![]() (1,2,2)
цієї площини.
(1,2,2)
цієї площини.
Розв’язання
Обчислимо потік векторного поля через поверхню піраміди (рис.1) за допомогою формули Остроградсько-Гаусса :
Ц =
=
![]() .
.
1/2
Z
С
В




Y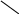

1/2




А
Мал. 1
1/2
X
У нашому
випадку
![]() ,
,
![]() .
.
Отже ,
Ц =
![]()
![]()
![]() .
.
Обчислимо циркуляцію векторного поля :
Маємо
Ц =
![]() .
.
Обчислимо кожний із криволінійних інтегралів . На лінні AB(z=0, dz=0) x змінюється від 1 до 0 . Тому
![]()
На лінії
BC(x=0,
y=![]() -z,
dy=-dz)
z
змінюється від 0 до Ѕ . Тому
-z,
dy=-dz)
z
змінюється від 0 до Ѕ . Тому
![]()
На лініі CA (y=0 , dy=0) x змінюється від 0 до 1 . Тому
![]()
Звідси циркуляція
Ц =
![]() .
.
Додаток А
Запитання іспиту за 2 семестр
Невизначений інтеграл і його властивості. Таблиця невизначених інтегралів.
Методи безпосереднього інтегрування, заміни змінної і частинами.
Інтеграли виду
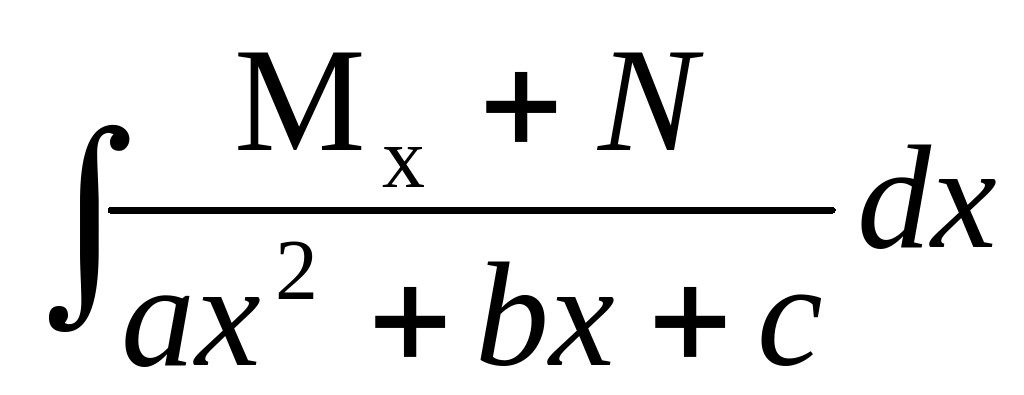 та
та

Розклад многочлена на лінійні множини і квадратні тричлени з дійсними коефіцієнтами.
Розклад правильного раціонального дробу на елементарні дроби.
Інтегрування елементарних дробів.
Інтеграли виду
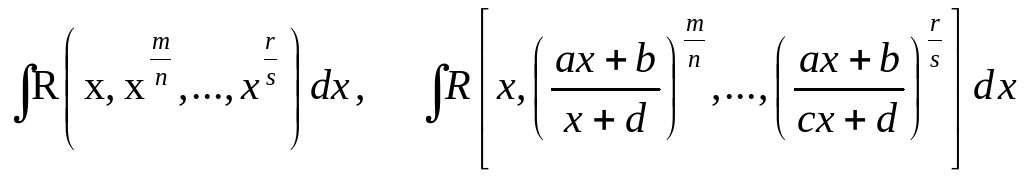
Інтеграл від диференціального бінома

Інтеграли виду
 Універсальна підстановка.
Універсальна підстановка.Інтеграли виду
 ,
,
 ,
,
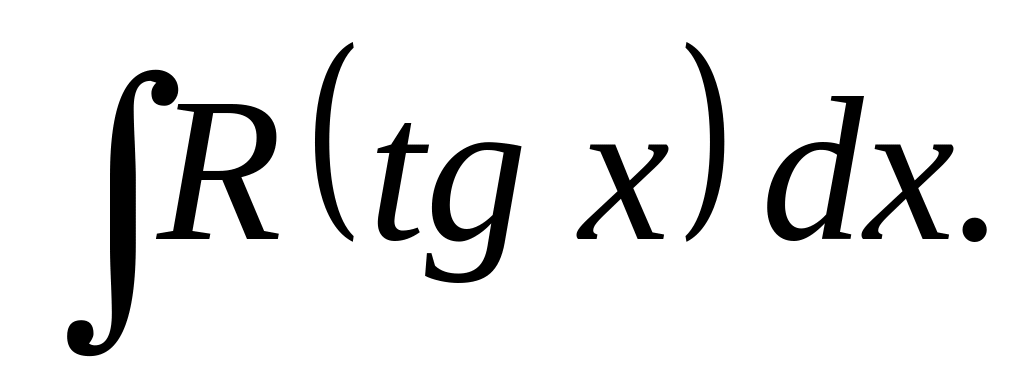
Інтеграли виду

Інтеграли виду
 .
.Інтеграли виду

Визначений інтеграл, та його властивості.
Теорема про похідну від інтеграла із змінною верхньою межею. Формула
Ньютона - Лейбніца.
Заміна змінної та інтегрування частинами у визначенному інтегралі.
Наближення обчислення визначених інтегралів.
Невласні інтеграли першого роду (з нескінченними межами).
Невласні інтеграли другого роду (від необмежених функцій).
Ознаки збіжності невласних інтегралів.
Інтеграли, залежні від параметра. Сформулювати теореми про неперервність, диференціювання та інтегрування інтеграла, залежного від параметра.
Гамма – і бета – функції. Зв`язок між ними.
Обчислення площ плоских фігур за допомогою визначеного інтеграла.
Обчислення довжин дуги кривої.
Обчислення об`єму тіла за площами його паралельних перетинів. Обчислення об`єма тіла обертання.
Обчислення площі тіла обертання.
Диференціальні рівняння (ДР), їх порядок та розв`язок .
ДУ першого порядку. Сформулювати теорему Коші про існування та єдність розв`язку рівняння у`= f (x,y). Задача Коші.
Загальний, частинний та особливий розв`язки ДР першого порядку. Геометричний зміст рівняння у`= f (x,y).
Рівняння з відокремлюваними змінними та однорідні.
Лінійні рівняння першого порядку. Рівняння Бернуллі.
Рівняння в повних диференціалах.
ДР n-го порядку. Сформулювати теорему про існування та єдність розв`язку. Задача Коші. Загальний та частинний розв`язки.
ДР, які допускають пониження порядку

Лінійне однородне диференціальне рівняння (ЛОДР). Властивості його розв`язків.
Лінійна незалежність функцій на проміжку (а, в). Визначник Веронського та його властивості.
Теорема про структуру загального розв`язку ЛОДР n – 10 порядку.
ЛОДР другого порядку із сталими коефіцієнтами . Характеристичне рівняння.
Лінійне неоднорідне диференціальне рівняння (ЛНДР) другого порядку. Теорема про структуру загального розв’язку ЛНДР.
Метод варіації довільних сталих.
ЛНДР другого порядку із сталими коефіцієнтами та правою частиною виду

Нормальні системи диференціальних рівнянь.
Наближене інтегрування рівняння
 методами Ейлера та Рунге-Кутта.
методами Ейлера та Рунге-Кутта.Числові ряди. Сума ряду. Найпростіші властивості числових рядів. Необхідна ознака збіжності ряду. Достатня ознака розбіжності ряду.
Достатні ознаки збіжності знакододатніх рядів. Ознаки порівняння, гранична ознака порівняння.
Ознаки Даламбера та Коші.
Інтегральна ознака Коші.
Знакочергуючі ряди. Ознака Лейбніца.
Знакозмінні ряди. Достатня ознака збіжності. Абсолютна та умовна збіжності.
Функціональні ряди. Область збіжності. Поняття рівномірної збіжності. Достатня ознака Вейєрштраса рівномірної збіжності.
Властивості рівномірно збіжних рядів.
Степеневі ряди. Теорема Абеля. Інтервал та радіус збіжності степеневого ряду. Властивості степеневих рядів.
Ряд Тейлора для функції f(x). Необхідні та достатні умови, за яких сума ряду Тейлора функції f(x) збігається з цією функцією.
Ряд Маклорена для функцій ex, sinx, cosx, (1+x)m, ln(1+x), arctgx.
Наближене інтегрування диференціальних рівнянь за допомогою степеневих рядів.
Тригонометричний ряд Фурє. Формули для коефіцієнтів Фурє. Достатні умови для зображення функції рядом Фурє.
Ряд Фурє для парних і непарних функцій, для функцій з довільним періодом.
Ряди Фурє для функцій, заданих на проміжку [0;l).
Ряд Фурє в комплексній формі.
Ряд Фурє за ортогональною системою функцій.
Інтеграл Фурє. Інтеграл Фурє для парних і непарних функцій.
Інтеграл Фурє в комплексній формі. Перетворення Фурє. Обернене перетворення Фурє. Косинус – і синус – перетворення Фурє.
Подвійний інтеграл, його властивості та обчислення у декартових координатах.
Заміна змінних у подвійному інтегралі. Якобіан. Подвійний інтеграл у полярних координатах.
Потрійний інтеграл, його властивості та обчислення.
Заміна змінних у потрійному інтегралі. Потрійний інтеграл у циліндричних та сферичних координатах.
Геометричні та механічні застосування кратних інтегралів.
Криволінійний інтеграл першого роду (по довжині дуги), його властивості та обчислення. Фізичний зміст.
Криволінійний інтеграл другого роду (по координатах), його властивості та обчислення. Фізичний зміст.
Застосування криволінійних інтегралів.
Формула Гріна.
Умови незалежності криволінійного інтеграла від форми шляху інтегрування.
Інтегрування повних диференціалів. Первісна функція.
Поверхневий інтеграл першого роду (по площі поверхні), його властивості та обчислення. Фізичний зміст.
Поверхневий інтеграл другого роду (по координатам), його властивості та обчислення.
Скалярне поле, поверхні та лінії рівня. Градієнт скалярного поля.
Векторне поле. Векторні лінії. Поток векторного поля.
Теорема Остроградського-Гаусса. Дивергенція векторного поля.
Циркуляція векторного поля. Теорема Стокса. Ротор векторного поля.
Потенціальне та соленоїдальне поля.
Оператор Гамільтона. Оператор Лапласа.
Оператор Лапласа в циліндричних і сферичних координатах.
