
ЗАГАЛЬНI ВКАЗIВКИ
Контрольнi завдання та методичнi вказiвки мiстять наступнi роздiли вищоi математики: невизначений та визначений iнтеграли; диференцiяльнi рiвняння; ряди; кратнi, криволiнiйнi i поверхневi iнтеграли; теорiя поля.
Перед виконанням контрольноi роботи треба досконало спрацювати теоретичний матерiал за рекомендованою лiтературою i розв’язати вiдповiднi завдання. Корисно також ознайомитися з методами розв’язання типових варiантiв. В додатках наведено запитання до iспиту, а також словник математичних термiнiв.
Контрольна робота
Задача 1 Знайти невизначені інтеграли.
1.а)![]() ; б)
; б)![]() ;
;
в)
![]() ; г)
; г)
![]() ;
;
2.а)![]() ; б)
; б)![]() ;
;
в)
![]() ; г)
; г)
![]() ;
;
3. а)![]() б)
б)
![]()
в)
![]() г)
г)

4. а)
![]() б)
б)
![]()
в)
![]() г)
г)
![]()
5. а)
![]() б)
б)
![]()
в)
![]() г)
г)
![]()
6. а)
![]() б)
б)
![]()
в)
![]() г)
г)

7. а)
![]() б)
б)
![]()
в)
![]() г)
г)
![]()
8. а)![]()
![]() б)
б)
![]()
в)![]() г)
г)![]()
9. а)
![]() б)
б)
![]()
в)
![]() г)
г)
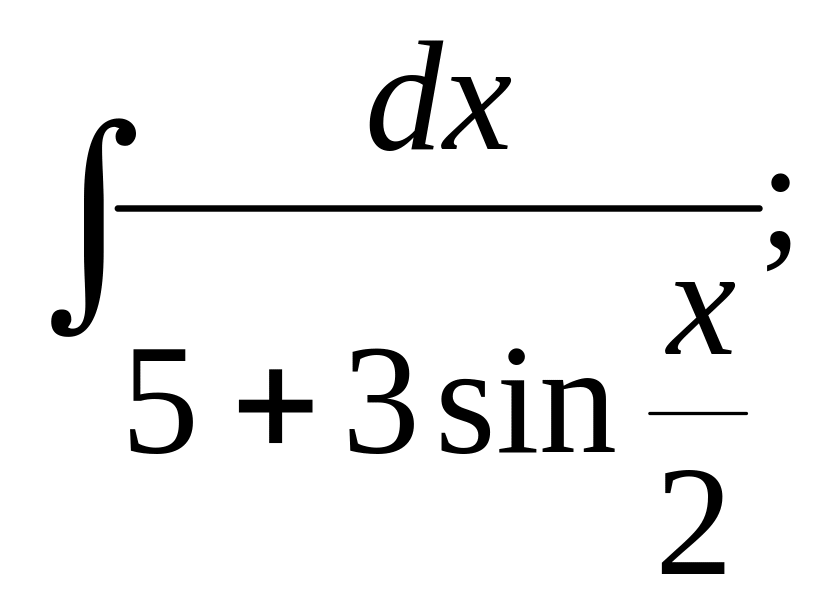
10. а)
![]() б)
б)
в)
![]() г)
г)
![]()
11. а)
![]() б)
б)
![]()
в)
![]() г)
г)
![]()
12. а)
![]() б)
б)
![]()
в)
![]() г)
г)
![]()
13. а)
![]() б)
б)
![]()
в)
![]() г)
г)
![]()
14. а)
![]() б)
б)
![]()
в)
![]() г)
г)
![]()
15. а)
![]() д)
д)
в)
![]() г)
г)
![]()
16.
а)![]() б)
б)
![]()
в)
![]() г)
г)
![]()
17. а)
![]() б)
б)
![]()
в)
![]() г)
г)
![]()
18. а)
![]() б)
б)
![]()
в)
![]() г)
г)
![]()
19. а)
![]() б)
б)
![]()
в)
![]() г)
г)
![]()
20.
а)![]() б)
б)
![]()
в)
 г)
г)
![]()
21.
а)![]() б)
б)
![]()
в)
 г)
г)
![]()
22.
а)![]() б)
б)
![]()
в)
![]() г)
г)
![]()
23. а)
![]() б)
б)
![]()
в)
![]() г)
г)
![]()
24.а)
![]() б)
б)
![]()
в)
![]() г)
г)
![]()
25.
a)![]() б)
б)
![]()
в)
![]() г)
г)
![]()
26. а)
![]() б)
б)
![]()
в)
![]() г)
г)
![]()
27. а)
![]() б)
б)
![]()
в)
![]() г)
г)
![]()
28. а)
![]() б)
б)
![]()
в)
![]() г)
г)
![]()
29.
а)![]() б)
б)
![]()
в)
![]() г)
г)
![]()
30. а)
![]() б)
б)
![]()
в)
![]() г)
г)
Задача 2 Обчислити невласні інтеграли або встановити їхню розбіжність
1. а)
![]() б)
б)

2. а)
![]() б)
б)
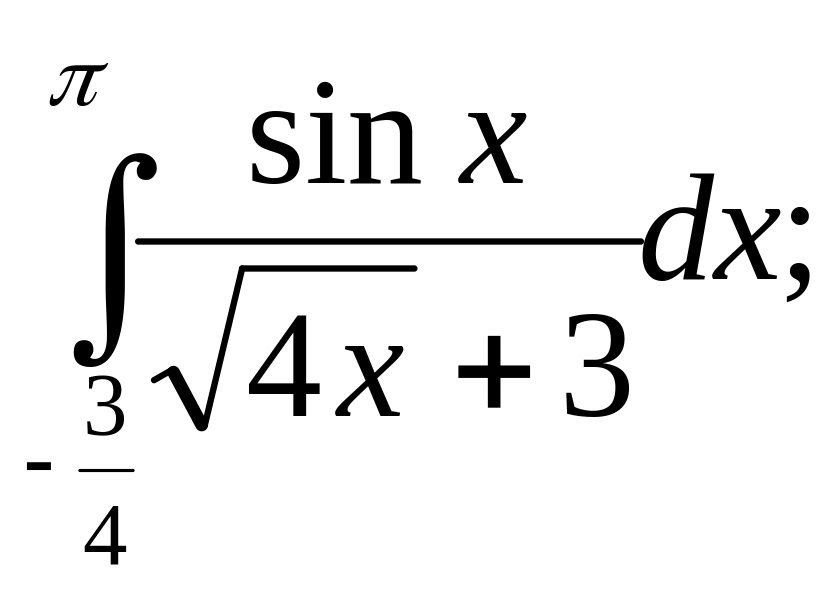
3. а)
![]() б)
б)
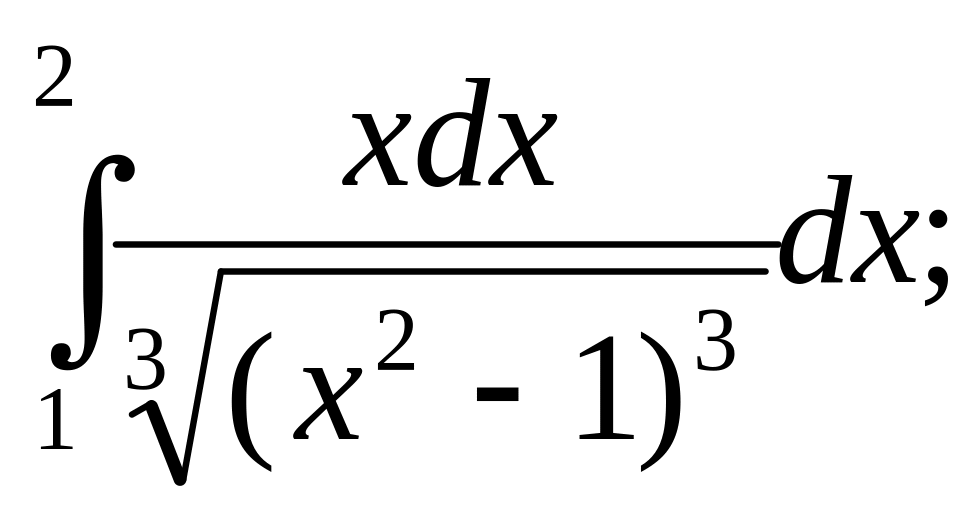
4. а)
 б)
б)
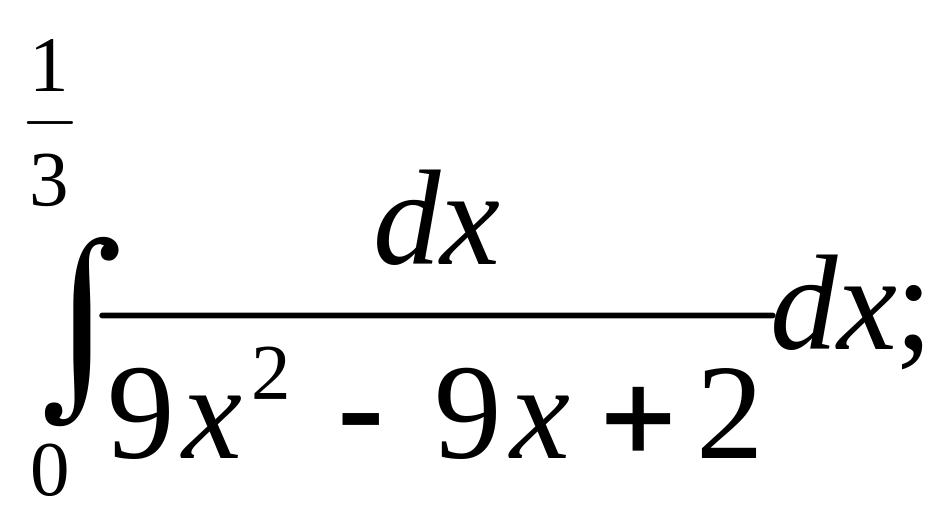
5. а)
![]() б)
б)
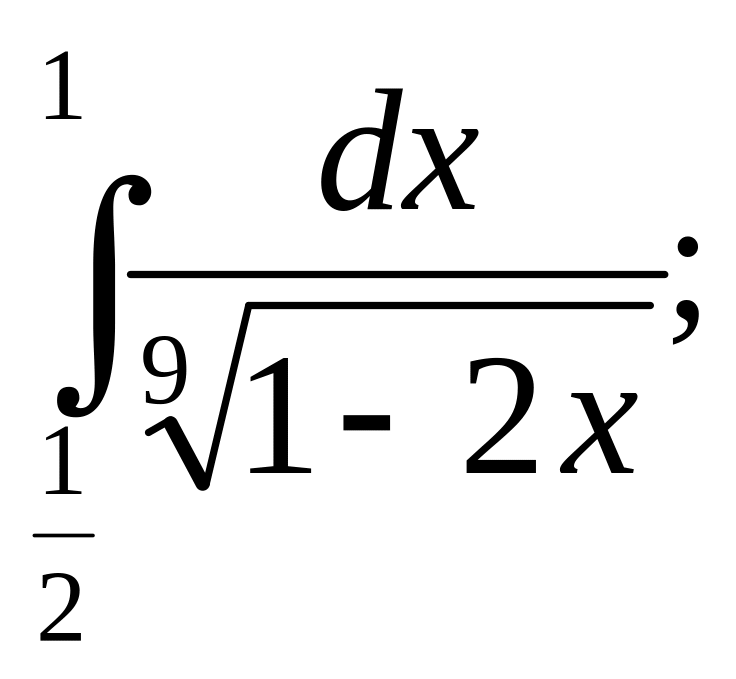
6. а)
![]() б)
б)

7. а)
![]() б)
б)
![]()
8. а)
![]() б)
б)
![]()
9. а)
![]() б)
б)
![]()
10. а)
![]() б)
б)
![]()
11. а)
![]() б)
б)

12.а)
![]() б)
б)

13. а)
![]() б)
б)

14. а)
![]() б)
б)
![]()
15. а)
![]() б)
б)

16.
а)![]() б)
б)

17. а)
![]() б)
б)

18. а)
![]() б)
б)

19. а)
![]() б)
б)
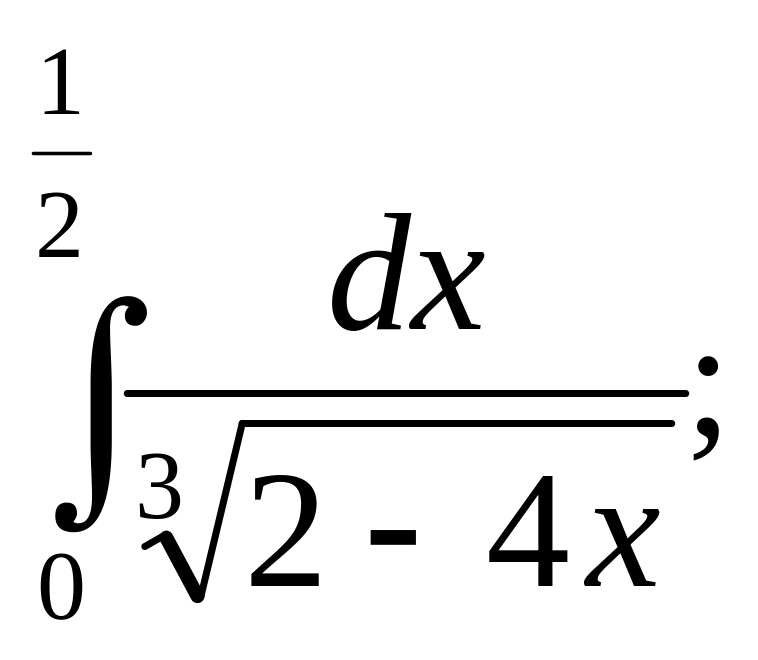
20. а)
![]() б)
б)
![]()
21. а)
![]() б)
б)

22. а)
![]() б)
б)

23. а)
 б)
б)

24. а)
![]() б)
б)
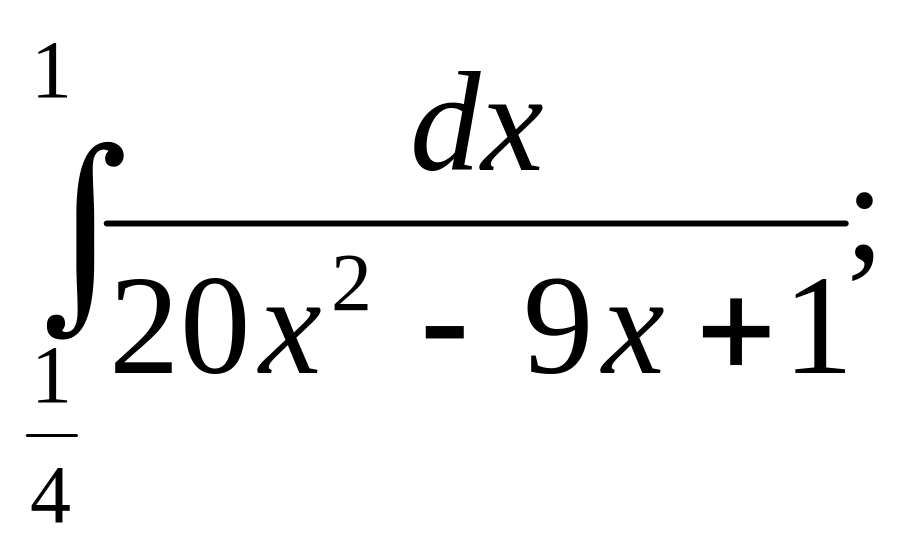
25. а)
![]() б)
б)

26. а)
![]() б)
б)

27. а)
![]() б)
б)
![]()
28. а)
![]() б)
б)
![]()
29. а)
 б)
б)

30. а)
![]() б)
б)

Задача 3 Обчислити площу фігури, обмеженої лініями:
1.
![]() 2.
2.
![]()
3.
![]() 4.
4.
![]()
5.
![]() 6.
6.
![]()
7.
![]() 8.
8.
![]()
![]()
9.
![]() 10.
10.
![]()
11.
![]() . 12.
. 12.
![]()
13.
![]() 14.
14.
![]()
![]()
![]()
Обчислити довжину дуги кривої, заданої рівняннями:
15.
![]() 16.
16.
![]()
17.
![]() 18.
18.
![]()
19.
![]() 20.
20.
![]()
![]()
21.
![]() 22.
22.
![]()
23.
![]() 24.
24.
![]()
![]()
25.
![]() 26.
26.
![]()
![]()
27.
![]() 28.
28.
![]()
![]()
29.
![]() 30.
30.
![]()
Задача 4 Обчислити площу поверхні, утворенної обертанням дуги кривої L навколо вказаної осію.
1.
![]() ,
полярна вісь. 2.
,
полярна вісь. 2.
![]() ,
полярна вісь.
,
полярна вісь.
3.
![]() . 4.
. 4.
![]() .
.
5.
![]() . 6.
. 6.![]() .
.
7.
![]() ,
полярна вісь. 8.
,
полярна вісь. 8.
![]() .
.
9.
![]() . 10.
. 10.
![]() .
.
11.
![]() ,
полярна вісь. 12.
,
полярна вісь. 12.
![]() .
.
13.
![]() ,
полярна вісь. 14.
,
полярна вісь. 14.
![]() .
.
15.
![]() . 16.
. 16.
![]() .
.
17.
![]() . 18.
. 18.
![]() ,
полярна вісь.
,
полярна вісь.
19.
![]() ,
полярна вісь. 20.
,
полярна вісь. 20.
![]()
21.
![]() . 22.
. 22.
![]() .
.
23.
![]() . 24.
. 24.
![]() ,
полярна вісь.
,
полярна вісь.
25.
![]() полярна
вісь. 26.
полярна
вісь. 26.
![]() .
.
27.
![]() . 28.
. 28.![]() .
.
29.
![]() . 30.
. 30.
![]() ,
полярна вісь.
,
полярна вісь.
Задача 5 Встановити тип диференціального рівняння і знайти загальний розв’язок.
1. а)
![]() б)
б)
![]()
2. а)
![]() б)
б)
![]()
3. a)
![]() б)
б)
![]() .
.
4. a)
![]() б)
б)
![]()
5. a)
![]() б)
б)
![]()
6. a)
![]() б)
б)
![]()
7. a)
![]() б)
б)
![]()
8. a)
![]() б)
б)
![]()
9. a)
![]() б)
б)
![]()
10. a)
![]() б)
б)
![]()
11. a)
![]() б)
б)
![]()
12. a)
![]() б)
б)
![]()
13. a)
![]() б)
б)
![]()
14. a)
![]() б)
б)
![]()
15.
a)![]() б)
б)
![]()
16. a)
![]() б)
б)
![]()
17. a)
![]() б)
б)
![]()
18. a)
![]() б)
б)
![]()
19. a)
![]() б)
б)
![]()
20. a)
![]() б)
б)
![]()
21. a)
![]() б)
б)
![]()
22. a)
![]() б)
б)
![]()
23. a)
![]() б)
б)
![]()
24. a)
![]() б)
б)
![]()
25. a)
![]() б)
б)
![]()
26. a)
![]() б)
б)
![]()
27. a)
б)
![]()
28. a)
 б)
б)
![]()
29. a)
![]() б)
б)
![]()
30. a)
![]() б)
б)
![]()
Задача 6 Знайти загальний або частинний розв’язок диференцiального рiвняння, яке допускае пониження порядку.
1. a)
![]() б)
б)
![]()
2. a)
![]() б)
б)
![]()
3. a)
![]() б)
б)
![]()
4. a)
![]() б)
б)
![]()
5. a)
![]() б)
б)
![]()
6. a)
![]() б)
б)
![]()
7. a)
![]() б)
б)
![]()
8. a)
![]() б)
б)
![]()
9. a)
![]() б)
б)
![]()
10. a)
![]() б)
б)
![]()
11. a)
![]() б)
б)
![]()
12. a)
![]() б)
б)
![]()
13. a)
![]() б)
б)
![]()
14. a)
![]() б)
б)
![]()
15. a)
![]() б)
б)
![]()
16. a)
![]() б)
б)
![]()
17. a)
![]() б)
б)
![]()
18. a)
![]() б)
б)
![]()
19. a)
![]() б)
б)
![]()
20. a)
![]() б)
б)
![]()
21. a)
![]() б)
б)
![]()
22. a)
![]() б)
б)
![]()
23. a)
![]() б)
б)
![]()
24. a)
![]() б)
б)
![]()
25. a)
![]() б)
б)
![]()
26. a)
б)
![]()
27. a)
![]() б)
б)
![]()
28. a)
![]() б)
б)
![]()
29. a)
![]() б)
б)
![]()
30. a)
![]() б)
б)
![]()
Задача 7 Розв’язати задачу Кошi.
1.
![]()
2.
![]()
3.
![]()
4.
![]()
5.
![]()
6.
![]()
7.
![]()
8.
![]()
9.
![]()
10.
![]()
11.
![]()
12.
![]()
13.
![]()
14.
![]()
15.
![]()
16.
![]()
17.
![]()
18.
![]()
19.
![]()
20.
![]()
21.

22.
![]()
23.
![]()
24.
![]()
25.
![]()
26.
![]()
27.
![]()
28.
![]()
29.
![]()
30.
![]()
Задача 8 а)дослiдити на збiжнiсть числовий ряд; б)знайти область збiжностi функцiонального ряду.
1. a)
![]() б)
б)
![]()
2. a)
![]() б)
б)
![]()
3. a)
![]() б)
б)
![]()
4. a)
![]() б)
б)
![]()
5. a)
![]() б)
б)
![]()
6. a)
![]() б)
б)
![]()
7. a)
![]() б)
б)
![]()
8. a)
![]() б)
б)
![]()
9. a)
![]() б)
б)
![]()
10. a)
![]() б)
б)
![]()
11. a)
![]() б)
б)
![]()
12. a)
![]() б)
б)
![]()
13. a)
![]() б)
б)
![]()
14. a)
![]() б)
б)
![]()
15. a)
![]() б)
б)
![]()
16. a)
![]() б)
б)
![]()
17. a)
![]() б)
б)
![]()
18. a)
![]() б)
б)
![]()
19. a)
![]() б)
б)
![]()
20. a)
![]() б)
б)
![]()
21. a)
![]() б)
б)
![]()
22. a)
![]() б)
б)
![]()
23. a)
![]() б)
б)
![]()
24. a)
![]() б)
б)
![]()
25. a)
![]() б)
б)
![]()
26. a)
![]() б)
б)
![]()
27. a)
![]() б)
б)
![]()
28. a)
![]() б)
б)
![]()
29. a)
![]() б)
б)
![]()
30. a)
![]() б)
б)
![]()
Задача 9 Розкласти функцiю y=f(x) в ряд Фур’є в заданому iнтервалi (a,b).
1.
![]() 2.
2.
![]()
3.
![]() 4.
4.
![]()
5.
![]() 6.
6.
![]()
7.
![]() 8.
8.
![]()
9.
![]() 10.
10.
![]()
11.
![]() 12.
12.
![]()
13.
![]() 14.
14.
![]()
15.
![]() 16.
16.
![]()
17.
![]() 18.
18.
![]()
19.
![]() 20.
20.
![]()
21.
![]() в ряд косинусiв.
22.
в ряд косинусiв.
22.
![]() в ряд синусiв.
в ряд синусiв.
23.
![]() в ряд косинусiв.
24.
в ряд косинусiв.
24.
![]() в ряд синусiв.
в ряд синусiв.
25.
![]() в ряд синусiв.
26.
в ряд синусiв.
26.
![]() в ряд косинусiв.
в ряд косинусiв.
27.
![]() в ряд косинусiв.
28.
в ряд косинусiв.
28.
![]() в ряд синусiв.
в ряд синусiв.
29.
![]() в ряд синусiв.
30.
в ряд синусiв.
30.
![]() в ряд косинусiв.
в ряд косинусiв.
Задача 10 Обчислити подвiйний iнтеграл, використовуючи полярнi координати.
1.
![]()
2.
![]()
3.
![]()
4.
![]()
5.
![]()
6.
![]()
7.
![]()
8.
![]()
9.
![]()
10.
![]()
11.
![]()
12.
![]()
13.
![]()
14.
![]()
15.
![]()
16.
![]()
17.
![]()
18.
![]()
19.
![]()
20.
![]()
21.
![]()
22.
![]()
23.
![]()
24.
![]()
25.
![]()
26.
![]()
27.
![]()
28.
![]()
29.
![]()
30.
![]()
Задача 11 Знайти масу тiла, розмiщеного в об’ємi V, якщо - густина.
1.
![]()
2.
![]()
3.
![]()
4.
![]()
5.
![]()
6.
![]()
7.
![]()
8.
![]()
9.
![]()
10.
![]()
11.
![]()
12.
![]()
13.
![]()
14.
![]()
15.
![]()
16.
![]()
17.
![]()
18.
![]()
19.
![]()
20.
![]()
21.
![]()
22.
![]()
23.
![]()
24.
![]()
25.
![]()
26.
![]()
27.
![]()
28.
![]()
29.
![]()
30.
![]()
Задача 12 Обчислити криволiнiйний iнтеграл.
1.
![]() де LAB
– дуга астроiди,
x
= cos3t,
y
= sin3t
вiд
точки А(2,0) до точки В(0,2).
де LAB
– дуга астроiди,
x
= cos3t,
y
= sin3t
вiд
точки А(2,0) до точки В(0,2).
2.
![]() де L
– дуга кривой x
= t
cos
t,
y
= t
sin
t,
z
= t,
0
t
2.
де L
– дуга кривой x
= t
cos
t,
y
= t
sin
t,
z
= t,
0
t
2.
3.
![]() де
LOBA
–
ламана
OBA: O(0,0,0); B(0,2,0); A(0,2,1).
де
LOBA
–
ламана
OBA: O(0,0,0); B(0,2,0); A(0,2,1).
4.
![]() де L
– коло x2
+ y2
+ z2
= a2,
y
= x.
де L
– коло x2
+ y2
+ z2
= a2,
y
= x.
5.
![]() де L
– коло x
= 2 cos
t,
y
= 2 sin
t,
при додатному напрямi
обходу.
де L
– коло x
= 2 cos
t,
y
= 2 sin
t,
при додатному напрямi
обходу.
6.
![]() де L
– коло x2
+ y2
=4.
де L
– коло x2
+ y2
=4.
7.
![]() де
L – дуга
циклоiди
y = a(1-cos t), x = a(t – sin t), /6
t
/3.
де
L – дуга
циклоiди
y = a(1-cos t), x = a(t – sin t), /6
t
/3.
8.
![]() де L
– чверть кола x2
+ y2
+ z2
= R,
x2
+ y2
= R2/4,
яка знаходиться в першому октантi.
де L
– чверть кола x2
+ y2
+ z2
= R,
x2
+ y2
= R2/4,
яка знаходиться в першому октантi.
9.
![]() де L
– дуга елiпса
x
= 2 cos
t,
y
= 2 sin
t
при додатному напрямi
обходу.
де L
– дуга елiпса
x
= 2 cos
t,
y
= 2 sin
t
при додатному напрямi
обходу.
10.
![]() де
L
– дуга кардiоiди
= 2(1 + cos
),
0
/2.
де
L
– дуга кардiоiди
= 2(1 + cos
),
0
/2.
11.
![]() де LOA
– дуга параболи z
= x2
/ 4, вiд
точки О(0,0,0) до точки А(2,0,1).
де LOA
– дуга параболи z
= x2
/ 4, вiд
точки О(0,0,0) до точки А(2,0,1).
12.
![]() де
L – дуга
елiпса
x = a cos t, y = a sin t, z = bt, 0t2.
де
L – дуга
елiпса
x = a cos t, y = a sin t, z = bt, 0t2.
13.
![]() де LАВ
– дуга елiпса
x
= cos
t,
y
= 2 sin
t,
вiд
точки А(1,)) до точки В(0,2).
де LАВ
– дуга елiпса
x
= cos
t,
y
= 2 sin
t,
вiд
точки А(1,)) до точки В(0,2).
14.
![]() де L
– дуга астроiди
x
= cos3
t,
y
= sin3
t,
яка знаходиться мiж
точками А(1,0) i
В(0,2).
де L
– дуга астроiди
x
= cos3
t,
y
= sin3
t,
яка знаходиться мiж
точками А(1,0) i
В(0,2).
15.
![]() де LAB
– вiдрiзок
прямой, який з’еднуе точки А(2,0,-2) i
В(-2,0,2).
де LAB
– вiдрiзок
прямой, який з’еднуе точки А(2,0,-2) i
В(-2,0,2).
16.
![]() де L
– першiй
звiй
конiчноi
гвинтовоi
лiнii,
x=tcost,
y
= t
sin
t,
z
= t.
де L
– першiй
звiй
конiчноi
гвинтовоi
лiнii,
x=tcost,
y
= t
sin
t,
z
= t.
17.
![]() де LOA
– дуга кола
x
= R
cos
t,
y
= R
sin
t;
O(R,0);A(0<r).
де LOA
– дуга кола
x
= R
cos
t,
y
= R
sin
t;
O(R,0);A(0<r).
18.
де L
– дуга кривой x
= cos
t,
y
= sin
t,
![]() ,
0t2.
,
0t2.
19.
![]() де L
– дуга елiпса
x
= a
cos
t,
y
= sin
t,
при доданому напрямi
обходу.
де L
– дуга елiпса
x
= a
cos
t,
y
= sin
t,
при доданому напрямi
обходу.
20.
![]() де L
– перший звiй
лемнiскати
де L
– перший звiй
лемнiскати
![]()
21.
![]() де LAB–
вiдрiзок
прямой АВ:А(1,1,1);В(2,3,4).
де LAB–
вiдрiзок
прямой АВ:А(1,1,1);В(2,3,4).
22.
![]() де L
- дуга кардiоiди
де L
- дуга кардiоiди
![]()
23.
![]() де L
– контур трикутника, утвореного прямими
y
= x,
x
= 2, y
= 0 при додатному напрямi
обходу контура.
де L
– контур трикутника, утвореного прямими
y
= x,
x
= 2, y
= 0 при додатному напрямi
обходу контура.
24.
де L
– чверть кола
![]() яка
знаходиться в першому октантi.
яка
знаходиться в першому октантi.
25.
![]() де LAB
– дуга одного звою гвинтовоi
лiнii
x=cos
t,
y
= sin
t,
z
= 2t;
A(1,0,0);
B
= (1,0,4).
де LAB
– дуга одного звою гвинтовоi
лiнii
x=cos
t,
y
= sin
t,
z
= 2t;
A(1,0,0);
B
= (1,0,4).
26.
![]() де L
– коло
де L
– коло
![]()
27.
![]() де LАВ
– будь – яка лiнiя
вiд
точки А(/4,2)
до точки В(/6,1).
де LАВ
– будь – яка лiнiя
вiд
точки А(/4,2)
до точки В(/6,1).
28.
![]() де L
– дуга параболи
де L
– дуга параболи
![]() вiдтята
параболою
вiдтята
параболою
![]()
29.
![]() де L
– контур трикутника з вершинами А(0,0),
В(1,0), С(0,1) при додатному напрямi
обходу контура.
де L
– контур трикутника з вершинами А(0,0),
В(1,0), С(0,1) при додатному напрямi
обходу контура.
30.
![]() де L
– коло
де L
– коло
![]()
Задача 13
Обчислити: 1)поток векторного поля
![]() через
зовнiшню
поверхню пiрамiди,
утвореноi
площиною (P)
i
координатними площинами; 2)циркуляцiю
векторного поля
по
контуру трикутника, отриманого в
результатi
перетину
площини (Р): Ax+By+Cz=D
з координатними площинами при додатному
напрямi
обходу вiдносно
нормального вектора
через
зовнiшню
поверхню пiрамiди,
утвореноi
площиною (P)
i
координатними площинами; 2)циркуляцiю
векторного поля
по
контуру трикутника, отриманого в
результатi
перетину
площини (Р): Ax+By+Cz=D
з координатними площинами при додатному
напрямi
обходу вiдносно
нормального вектора
![]() цiєї
площини.
цiєї
площини.
1.
![]()
2.
![]()
3.
![]()
4.
![]()
5.
![]()
6.
![]()
7.
![]()
8.
![]()
9.
![]()
10.
![]()
11.
![]()
12.
![]()
13.
![]()
14.
![]()
15.
![]()
16.
![]()
17.
![]()
18.
![]()
19.
![]()
20.
![]()
21.
![]()
22.
![]()
23.
![]()
24.
![]()
25.
![]()
26.
![]()
27.
![]()
28.
![]()
29.
![]()
30.
![]()
