1. Общие сведения

   1. Постановка задачи условной оптимизации функции многих переменных

      1. Общая постановка задачи

, .

При задача называется задачей со смешанными ограничениями, при- задачей с ограничениями неравенствами, а при- задачей с ограничениями равенствами.

2. Функция Лагранжа

Функция называется обобщенной функцией Лагранжа, числа- множителями Лагранжа. Классической функцией Лагранжа называется функция.

3. Градиент функции Лагранжа

Градиентом обобщенной функции Лагранжа по называется вектор-столбец:

.

4. Первый дифференциал ограничения

Первым дифференциалом ограничения называется функция.

5. Второй дифференциал обобщенной функции Лагранжа

Вторым дифференциалом обобщенной функции Лагранжа называется функция .

ПРИМЕР: ,

Градиенты ограничений ,…,являются линейно независимыми в точке, если равенствовыполняется только при.

2. Решение задачи условной оптимизации функции при ограничениях типа равенств с использованием необходимых и достаточных условий

   1. Необходимые и достаточные условия условного экстремума при ограничениях равенствах

Пусть даны дважды непрерывно дифференцируемые целевая функция и функции ограничений, определяющие множество допустимых решений. Тогда задача оптимизации имеет вид:

, .

Эта задача может быть решена как задача безусловной оптимизации (при Kn), если исключить из целевой функцииKнезависимых переменных с помощью заданных равенств, т. е. задача сводится к виду:

При этом размерность задачи уменьшается с nдоn-K. Однако такой метод применим лишь в тех случаях, когда уравнение-ограничение можно разрешить относительно некоторого набора независимых переменных.

Более универсальный способ основан на использовании функции Лагранжа:

После этого задача условной оптимизации с ограничениями равенствами сводится к задаче безусловной оптимизации:

Найти ,,

При этом учитывается, что:

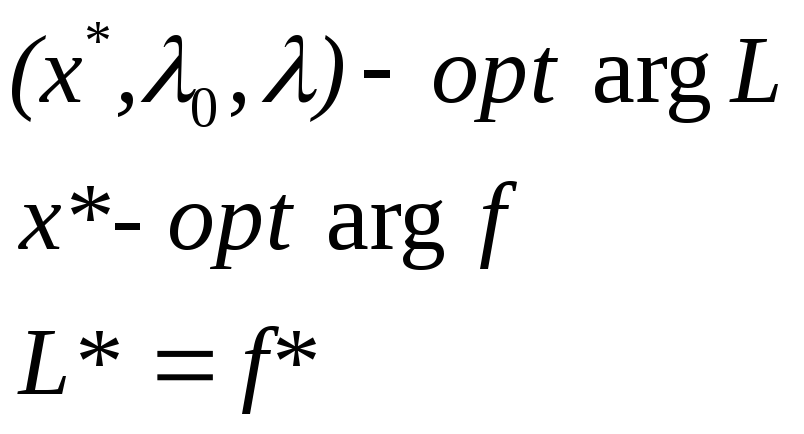
1. Необходимые условия экстремума первого порядка

Пусть есть точка локального экстремума. Тогда найдутся числа, не равные одновременно нулю и такие, что выполняются следующие условия:

1. условие стационарности обобщенной функции Лагранжа по :

,

2. условие допустимости решения

,

Если при этом градиенты в точкелинейно независимы, то.

Система содержит уравнений инеизвестное,,. Точкиудовлетворяющие системе при некоторых,называются условно-стационарными.

При решении задач проверка условия регулярности затруднена, т.к. точка заранее не известна. Поэтому, как правило, рассматриваются два случая:и. Если, то полагают, что, тогда обобщенная функция Лагранжа становится классической функцией Лагранжа.

Случай отражает вырожденность ограничений. Точка экстремумаприназывается регулярной, а при- нерегулярной.

2. Необходимые условия экстремума второго порядка

Пусть - регулярная точка минимума (максимума) и имеется решение. Тогда второй дифференциал классической функции Лагранжа, вычисленный в точке, неотрицателен, неположителен:

()

для всех , таких что

,

3. Достаточные условия экстремума

Пусть имеется решение . Если в этой точке() для всех ненулевыхтаких, что

,

то точка является точкой локального минимума(максимума).