
- •Общие сведения
- •Постановка задачи безусловной оптимизации функции многих переменных
- •Глобальный оптимум функции
- •Локальный оптимум функции
- •Выпуклость множеств и функций
- •Методы прямого поиска безусловного оптимума функции многих переменных
- •Эвристические методы
- •Метод Хука-Дживса (метод прямого поиска)
- •Метод покоординатного спуска
- •Метод Розенброка (метод вращающихся координат)
- •Метод Нелдера-Мида
- •Теоретические методы прямого поиска
- •Метод сопряженных направлений (метод Пауэлла)
- •Решение задачи безусловной оптимизации функции многих переменных с использованием необходимых и достаточных условий экстремума
- •Методы оптимизации функции одной переменной
- •Метод квадратичной интерполяции
- •Метод Пауэлла (квадратичной интерполяции)
- •Метод первого приемлемого значения (квадратичная интерполяция с использованием производных).
- •Метод кубической интерполяции (Давидона)
- •Методы оптимизации функции многих переменных
- •Общие критерии останова численных методов оптимизации функции многих переменных
- •Модельная схема применения методов оптимизации функции многих переменных
- •Градиентные методы
- •Аффинная (линейная) модель функции многих переменных
- •Метод Коши
- •Расчет направления поиска методами сопряженных градиентов
- •Метод Ньютона-Рафсона
- •Метод Марквардта
- •Методы переменной метрики (квазиньютоновские методы)
- •Соотношение секущих
- •Метод bfgs
- •Метод dfp
Метод Ньютона-Рафсона
Усовершенствованием метода Ньютона является использование процедуры определения шага при использовании Ньютоновского напрвавления:
![]()
Такой метод называется методом Ньютона-Рафсона и сходится независимо от выбора начальной точки с квадратичной скоростью.
Метод Марквардта
Альтернативой
методу Ньютона является метод Марквардта,
который основан на введении в квадратичную
модель дополнительного члена
![]() для учета членов разложения Тейлора
более высоких порядков. Итерационная
формула метода Марквардта выглядит
следующим образом:
для учета членов разложения Тейлора
более высоких порядков. Итерационная
формула метода Марквардта выглядит
следующим образом:
![]() ,
,
Где
![]() ,k=0,1,2,… последовательность
положительных чисел таких, что матрица
,k=0,1,2,… последовательность
положительных чисел таких, что матрица![]() положительно определена. Как правило,
число
положительно определена. Как правило,
число![]() назначается на порядок больше, чем самый
большой элемент матрицы
назначается на порядок больше, чем самый
большой элемент матрицы![]() ,
а в ряде стандартных программ полагается
,
а в ряде стандартных программ полагается![]() .
.
Алгоритм метода Марквардта выглядит следующим образом:
Задать
 ,
, ,
, - предельное число итераций,
- предельное число итераций, .
.
Вычислить

Проверить условия остановки. Если хотя бы одно условие остановки выполняется, то оптимум найден

Вычислить

Вычислить

Вычислить

Вычислить

Вычислить

Проверить выполнение условия
 :
:Если условие выполняется, то перейти к шагу 11
Если условие не выполняется, то перейти к шагу 12
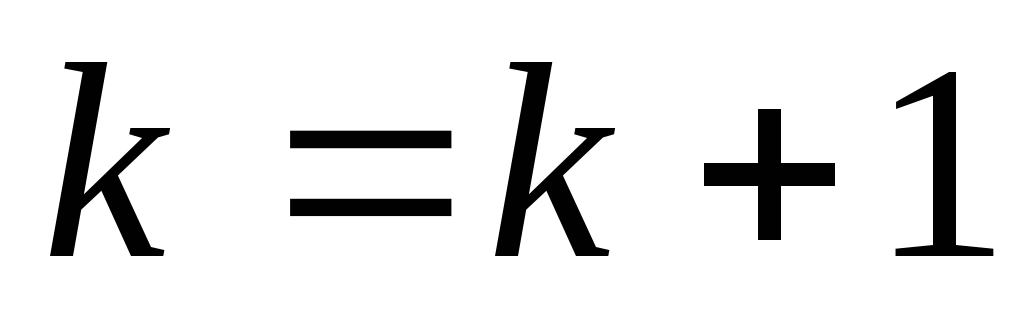 ,
,
 ,
переход к шагу 3.
,
переход к шагу 3. ,
переход к шагу 6.
,
переход к шагу 6.
В окрестностях точки оптимума метод Марквардта обладает скоростью сходимости близкой к квадратичной.
Методы переменной метрики (квазиньютоновские методы)
Соотношение секущих
Предположим, что матрица Гессе неизвестна, тогда можно использовать ее аппроксимацию Н(k). Тогда квадратичная модель функции имеет вид:
![]()
![]() .
.
![]() .
.
Получаем следующую формулу расчета направления:
![]() .
.
Тогда итерационная формула имеет вид:
![]() .
.
При
условии, что
![]() получаем:
получаем:
![]()
![]() .
.
Или
![]()
Обозначим
![]() и
и![]() .
Тогда соотношение секущих (квазиньютоновское
условие) для оптимизации функции многих
переменных имеет вид:
.
Тогда соотношение секущих (квазиньютоновское
условие) для оптимизации функции многих
переменных имеет вид:
![]()
Для
обеспечения сходимости метода матрица
![]() должна быть симметричной и положительно
определенной.
должна быть симметричной и положительно
определенной.
Способы пересчета H(k+1)породили ряд методов, которые называются квазиньютоновскими методами или методами переменной метрики.
Наиболее эффективными из этих методов являются метод BFGSиDFP.
Метод bfgs
В
методе BFGSиспользуется
следующая формула пересчета матрицы![]() :
:
![]()
![]()
Эта формула гарантирует симметричность и положительную определенность матрицы на каждом шаге алгоритма. Формула называется формулой BFGS- Бройдена-Флетчера-Гольдфарба-Шанно.
На
первой итерации матрица
![]() выбирается единичной матрицей.
выбирается единичной матрицей.
Метод dfp
В
методе DFPвычисляется не
аппроксимация![]() матрицы
матрицы![]() ,
а сразу аппроксимация
,
а сразу аппроксимация![]() матрицы
матрицы![]() ,
а формулаDFP(Давидона-Флетчера-Пауэлла) имеет вид:
,
а формулаDFP(Давидона-Флетчера-Пауэлла) имеет вид:
![]() .
.
Формула
DFPпри аналитическом
вычислении шага поиска![]() обеспечивает сходимость метода для
квадратичных функций не более чем за
обеспечивает сходимость метода для
квадратичных функций не более чем за![]() шагов. Для неквадратичных функций
сходимость метода зависит от точности
решения задачи вычисления шага поиска.
шагов. Для неквадратичных функций
сходимость метода зависит от точности
решения задачи вычисления шага поиска.
Методы BFGSиDFPобладают сверхлинейной скоростью сходимости близкой к квадратичной.
