ИССЛЕДОВАНИЕ КОРРЕЛЯЦИОННО-ЭКСТРЕМАЛЬНОЙ СИСТЕМЫ НАВИГАЦИИ ПО КАРТАМ ГЕОФИЗИЧЕСКИХ ПОЛЕЙ

Цель работы: изучение принципов работы и экспериментальное иссле­дование корреляционно-экстремальных навигационных систем (КЭНС) по картам геофизических полей.

1. Теоретические сведения

В настоящее время интенсивно развивается теория и практика авто­матических систем навигации по геофизическим полям, в полной мере удовлетворяющих всей совокупности требований, предъявляемых к совре­менным средствам навигации летательных аппаратов .

Автоматическая навигация по геофизическим полям с определением местоположения основана на сопоставлении текущего изображения (ТИ), получаемого с помощью бортовой системы наблюдения поля (датчика поля), с информацией о поле или опорном "эталонном" изображении (ЭИ), храня­щейся в бортовой памяти. Сопоставление осуществляется обычно посредс­твом вычисления некоторого функционала типа корреляционной функции (КФ) и поисковым или беспоисковым нахождением экстремума этой характе­ристики.

В последнее время КЭНС находят широкое признание и применение. Они имеют разнообразную структуру и могут иметь различное предназначе­ние. Одним из удобных способов классификации КЭНС является классифика­ция по объему или характеру полезной информации, снимаемой с навигаци­онного поля бортовым датчиком в каждый момент времени или за короткий цикл сканирования. В соответствии с этим КЭНС делятся на три основных класса (рис. 1):

КЭНС-I - в системах этого класса рабочая информация в текущий мо­мент времени снимается в "точке", т.е. выходной сигнал датчика поля представляет скалярную величину;

КЭНС-II - для систем данного класса характерным является то, что бортовой датчик за короткий цикл сканирования мгновенно снимает информацию о поле вдоль произвольных, но заранее выбранных, линий. Та­ковыми, в частности, могут служить линии, перпендикулярные к продоль­ной (в случае поперечного сканирования антенной зондируемой поверхнос­ти) или поперечной (при продольном сканировании) оси летательного аппарата;

КЭНС-III - к этому классу относятся системы, в которых рабочая информация снимается с участка площади земной поверхности ("кадра"), просматриваемого бортовой системой в каждый момент времени или за короткий цикл сканирования (КЭНС с сопоставлением изображений).

По методу определения отклонения от экстремума КЭНС подразделяются на эвристические, поисковые, беспоисковые оптимальные (субоптимальные) и комбинированные. Такая классификация в некоторой мере соответс­твует алгоритмам КЭНС, которые могут быть реализованы в КЭНС-I, КЭНС-П и КЭНС-III на базе аналоговой, аналого-цифровой и цифровой тех­ники.

В теоретических исследованиях и математическом моделировании на первом этапе развития теории и разработки КЭНС рассматривалась, в ос­новном, четырехточечная дифференциальная схема формирования сигналов коррекции отклонения от экстремума КФ[1].

Главным недостатком дифференциального беспоискового алгоритма яв­ляется потеря работоспособности системой при начальных рассогласовани­ях, превышающих радиус корреляции поля, а также при нестационарности поля по дисперсии, математическому ожиданию и спектру.

Второе направление в развитии теории КЭНС составили поисковые ал­горитмы. Теория таких систем строится на основе широко известной теории статистических решений. Особенностью поисковых алгоритмов

является отсутствие ограничений на величину начальных ошибок навигационной системы.

Однако, реализация данных алгоритмов, особенно в случае решения задачи многопараметрического оценивания, требует значительной производительности бортовой цифровой вычислительной машины (БЦВМ). В данной лабораторной работе исследуется КЭНС-IIБ (см. рис. 1), которая является аналогом системы навигации по рельефу местности типа ТЕRСОМ. Метод навигации и наведения посредством сопоставления профилей рельефа местности ТЕRСОМ (Terrain Contour Matching) предназначен для применения на борту различных летательных аппаратов: пилотируемых и беспилотных самолетов, крылатых ракет, головных частей баллистических ракет. В основу метода построения системы ТЕRСОМ положен следующий принцип: географическое положение любой точки земной поверхности (су­ши) описывается единственным образом с помощью вертикальных профилей или топографией окружающей местности, аналогично тому, как каждый чело­век обладает своими неповторимыми отпечатками пальцев. Как и при ана­лизе отпечатков пальцев, такая система требует предварительного кар­тографирования или иного определения характеристик профилей поверхнос­ти того района, над которым система будет использоваться. Это может быть сделано, например, по стереоскопическим аэроснимкам местности с помощью известных в настоящее время способов. Предварительно опреде­ленные данные о рельефе района полетов запоминаются в цифровом виде в бортовом запоминающем устройстве.

Во время полета система ТЕRСОМ измеряет вертикальный профиль рельефа вдоль истинной траектории полета с помощью радиовысотомера (для измерения геометрической высоты полета) и баровысотомера (для по­лучения уровня отсчета профиля). Вычитая текущую высоту, измеренную радиовысотомером, из барометрической высоты ,система определяет профиль рельефа вдоль траектории полёта организует поиск в памяти вы­числителя наиболее "похожего", заранее запомненного профиля с извест­ными координатами. Поиск осуществляется последовательным сопоставлени­ем сигнала ТИ датчика поля с цифровым образом ЭИ и просмотром сначала назад и вперед предполагаемого местоположения, а затем поперек траек­тории в пределах матрицы размером 64 Х 64 ячейки (при размере ячейки ∆ от 30м Х 30м до 240м Х 240м).

Процедура сопоставления представляет собой минимизацию абсолютной разности, приближенно определяемой выражением

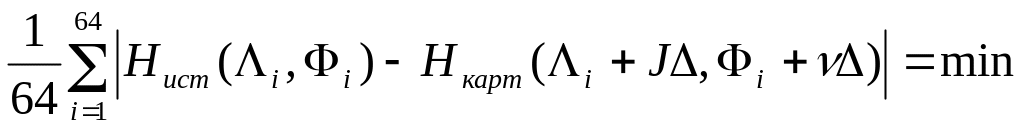
, где Н_ист -превышение рельефа вдоль истинной траектории полёта,

H_карт- превышение рельефа, выбранное из бортовой карты,

Λ_i, Φ_i- координаты летательного аппарата.

Конкретному исследованию в лабораторной работе подвергаются

качественные показатели обнаружения заданного участка ЭИ по предъявляемому ТИ в поисковой КЭНС.

В поисковых КЭНС проверяются гипотезы о возможных значениях оши­бок местоположения и скорости движущегося объекта. Для каждой проверя­емой гипотезы на основе измерений геофизического поля и ,имеющейся бор­товой карты этого поля, с использованием данных навигационной системы считываются значения функционала, являющегося мерой близости получен­ной в полете реализации поля и реализации поля, извлекаемой из блока памяти и соответствующей проверяемой гипотезе. Путем поиска экстремума функционала по всем проверяемым гипотезам определяются координаты мес­тоположения и скорость движения. Методы достижения экстремума функцио­нала могут быть различными.

Может применяться "слепой поиск", когда вводится дискретизация координат и значения функционала рассчитываются абсолютно для всех возможных. дискретных значений ошибок ГНС (главной навигационной, нап­ример инерциальной, системы). Такой метод поиска, являющийся в опреде­ленных условиях единственно возможным, надежно решает проблему ликви­дации больших начальных отклонений в КЭНС, хотя в некоторых случаях требует чрезмерно высокой производительности БЦВМ.

Другая группа методов поиска связана с вычислением градиентов (или их аналогов) функционала, определяющих направление движения к экстремуму. Здесь требования к быстродействию БЦВМ обычно оказываются ограниченными, так как не возникает необходимость рассчитывать значения функционалов для всевозможных ошибок ГНС, но возникают ограничения сходимости.

Рассмотрим эвристические поисковые алгоритмы одномерной КЭНС для оценки местоположения. Будем рассматривать равномерный горизонтальный полет. Пусть к текущему моменту времени t, когда принимается решение, проведено N измерений геофизического поля Z₁= f^*₁, ...,Z_N=f^*_N (рис. 2, а) и пусть в памяти БЦВМ записана карта поля f_n(x) (рис. 2, б).

В поисковых КЭНС производится запись в оперативное запоминающее устройство измеренных значений поля Z_i=f^*_i и, выдаваемых ГНС, координат местоположения x^*_i в момент проведения измерений. Пусть x^*_n - коорди­ната местоположения в момент последнего замера.

Эвристический алгоритм поисковой КЭНС сводится к следующему: наз­начается доверительный интервал 2Δ_max с центром в точке x^*_N. где Δ_mах-возможная максимальная ошибка ГНС.

Задается шаг дискретизации по коор­динате ΔI и в доверительном интервале с

этим шагом выбирается ряд дискретных точек. В дальнейшем

предполагается, что реальное положение летательного аппарата совпадает с одной из дискретных точек. В дейс­твительности это условие может и не выполняться.

Однако если величина ΔI невелика, введение дискретизации при проверке гипотез не приво­дит к существенным ошибкам. В рассматриваемом случае гипотезами H_i являются возможные дискретные значения iΔ1 продольной ошибки ГНС Δх (i =-n, ...,n; n=Δ_max/ΔI). Поскольку мы предположили отсутствие ошибки измерения скорости и постоянство Δх в процессе проведения измерений геофизического поля, то, с точностью до шумов датчика поля и ошибок картографирования, измеренная реализация совпадает с некоторым участком реализации навигационного поля, хранящейся в блоке памяти.

В процессе перебора различных возможных значений ошибок ГНС (т.е. проверки различных возможных гипотез H_i, состоящих в предположении, что ошибка Δх=iΔ1) из блока памяти извлекается для каждой проверяемой гипотезы соответствующая ей (гипотетическая) реализация поля:

{fn[x^*_N-iΔ1-(N-1)L],fn[x^*_N-iΔ1-(N-2)L],…,fn(x^*_N-iΔ1-L),fn(x^*_N-iΔ1)}. Сопоставляется гипотетическая реализация поля с измеренной:

Z₁=f[X_N-(N-1)L], ..., Z_N-1=f(X_N-L), Z_N=f(X_N),

где X_N - действительное местоположение ЛА в момент проведения последнего замера,

L - расстоя­ние, пролетаемое ЛА между последовательными измерениями. В результате такого сопоставления получается некоторое число I_i, которое характеризует степень совпадения измеренной и проверяемой гипотетической реали­зации. Величина I_i=I(H_i) зависит от измеренной и гипотетической реализаций навигационного поля. Кроме того,

I_i является функцией проверяе­мого значения Δx=iΔ1 ошибки навигационной системы.

Могут использоваться различные виды функционалов I_i, но они долж­ны обладать общим обязательным свойством: в идеальных условиях, при отсутствии ошибок измерения поля и картографирования и других возмуще­ний, функционал должен достигать абсолютного (глобального) экстремума на истинной гипотезе, т.е. при ΔX=X^*_N –X_N. Тогда и в условиях неизбеж­ных возмущений, рассчитав значения функционала для всех возможных зна­чений ошибки ГНС и, выбрав то значение ошибки Δх, при котором функцио­нал достиг экстремума, мы получим оценку местоположения, близкую к ис­тинной. Точность этой оценки будет тем выше, чем меньше ошибки измере­ния геофизического поля и больше длина обрабатываемой реализации (чис­ло измерений поля N).

В качестве функционалов в эвристических поисковых алгоритмах используются:

среднее произведение

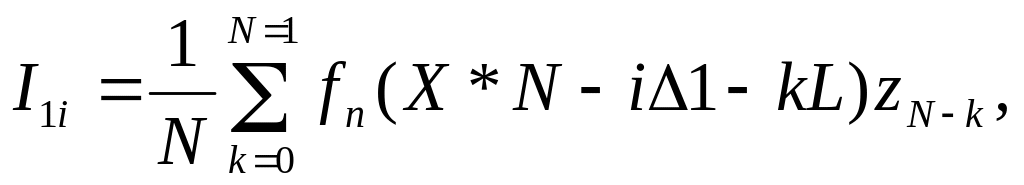
средняя абсолютная разность

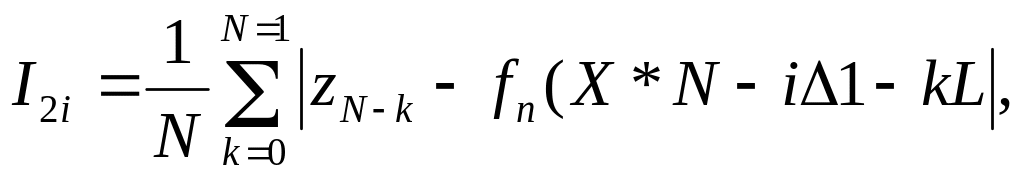
средний квадрат разности

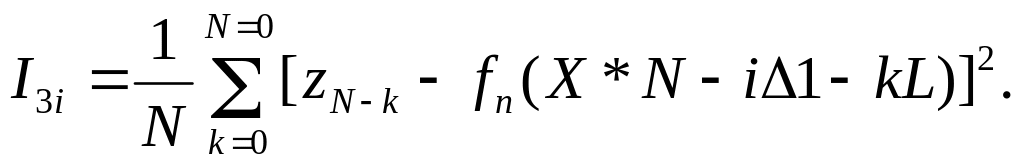
Если ошибки картографирования отсутствуют, т.е. в одних и тех же точках f_n(x)=f(x), где f(x) - истинное значение геофизического поля, а датчик поля производит измерения абсолютно точно Z_N-k=f(X_N-kL) , то выражения для функционалов принимают вид

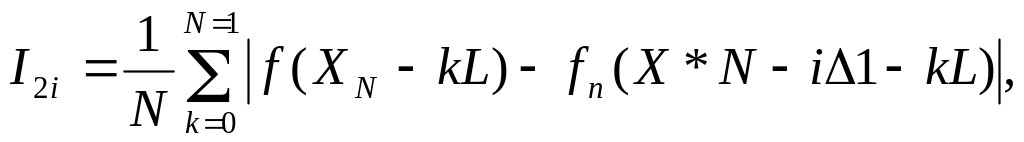
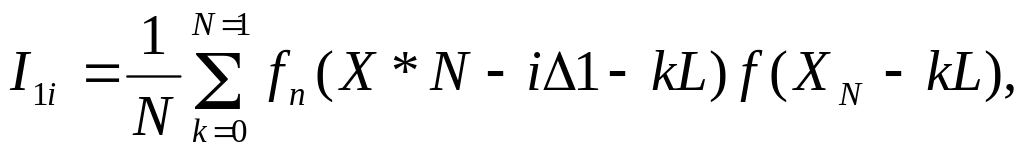
В идно, что все функционалы имеют абсолютный экстремум для прове­ряемой ошибки 1Δ1, совпадающей с действительной ошибкой ГНС ΔX=X^*_N-X_N. В этом случае I2i=I3i=0 и эти функционалы достигают абсолютного мини­мума. Функционал 1ц достигает на истинной гипотезе абсолютного макси­мума. Обоснованием функционала I1i является известное свойство корре­ляционной функции Rff(Δ) стационарного процесса f(x) достигать абсо­лютного максимума при нулевом сдвиге Δ=0. Действительно, если поле стационарное и эргодическое, а длина реализации NL достаточна для про­явления эргодичности, то

и абсолютный максимум I1i достигается при iΔ1=X*N-XN=ΔX. В лабораторной работе при экспериментальных исследованиях исполь­зуется алгоритм I1i.