5. Применение мми для изучения свойств числовых последовательностей

Пример 1.Вывести формулу суммы первых членов геометрической прогрессии , , …, , …; .

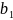Решение.

1. Докажем, что при ,

2. При имеем: . С другой стороны, . Значит, при равенство истинно.

3. Предположим, что , и докажем, что тогда справедливо равенство .

4. В самом деле, имеем: .

По принципу математической индукции заключаем, что равенство истинно при всех

Пример 2. Последовательность , , , …, , … определяется следующими условиями: , , . Докажем два свойства этой последовательности:

1. 

2. .

Решение 1.

1. Выпишем несколько первых членов последовательности. Имеем: , , 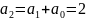, , . При 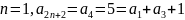. Значит, при утверждение 1) истинно.

2. Предположим, что оно истинно при , т.е. .

3. Докажем, что тогда оно верно и для , т.е.

В самом деле, воспользовавшись рекуррентным соотношением, получим: . Применив для формулу , получим: .

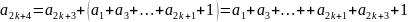Значит, доказываемое равенство выполняется для всех .

Решение 2.

1. Для утверждение справедливо: , так как , , .

2. Предположим, что .

3. Докажем, что тогда .

4. В самом деле, .

Тем самым интересующее нас свойство доказано.

Последовательность, о которой шла речь в только что рассмотренном примере, называется последовательностью Фибоначчи.

5. Применение мми для изучения свойств конечных множеств

Пример 1. Докажем, что если - конечные множеств, то . ( - декартово произведение множеств – множество, состоящее из всевозможных наборов указанного вида).

Решение.

1. ------------------------------------------------------------------------------

2. Предположим, что формула справедлива при , т.е. что выполняется равенство .

3. Докажем, что тогда формула верна при т.е. что выполняется равенство .

4. В самом деле, рассмотрим произвольный элемент ) множеств и положим 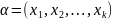. Очевидно, что между множеством наборов вида ( и множеством пар вида ) имеется взаимно однозначное соответствие, т.е. наборов вида столько же, сколько пар вида Если множество всех обозначить через , то можно сказать, что интересующее нас множество имеет столько же элементов, сколько множество , т.е. .

5. Но по доказанному выше для двух множеств и 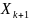имеем: , а по построению есть не что иное, как Воспользовавшись предположением индукции, получаем, что .

6. Значит, .

7. Тем самым формула доказана для всех натуральных чисел . Из нее, в частности, следует, что .

Это значит, что -я декартова степень -элементного множества 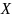содержит элементов.

Д оказанную формулу можно наглядно изобразить с помощью чертежей особого вида, называемых «деревьями» (рисунок 1). Пусть, например, множество состоит из четырех элементов: , а множество - из трех элементов: . Возьмем на плоскости какую-нибудь точку и проведем из нее четыре отрезка, соответствующие элементам множества . Из конца каждого отрезка проведем по три отрезка, соответствующих элементам множества . Тогда каждой паре ( соответствует начинающийся в точке путь, состоящий из двух отрезков. Если добавить еще множество , состоящее из пяти элементов, то из каждого конца отрезка, проведенного на втором шаге, надо будет провести еще по пять отрезков, всего получится 60 путей. Это число равно числу элементов декартового произведения .