Контрольные вопросы

1. Что такое массив?

2. Назовите основные характеристики (атрибуты) массива.

3. Как ввести и вывести массив?

4. Какого типа могут быть элементы массива?

5. Нужно ли указывать количество элементов в массиве при описании? Если да, то почему?

6. Какого типа может быть индекс в массиве?

7. Что может представлять собой индекс элемента в массиве?

8. Может ли индекс элемента в массиве принимать нулевое или отрицательное значение? Если да, то приведите пример описания такого массива.

9. Как обратиться к элементу массива?

10. Можно ли изменять количество элементов массива при выполнении программы?

11. Как поменять местами два элемента массива?

12. Что называется сортировкой массива? Какие методы сортировки Вы знаете?

13. В чем состоит метод попарно-обменной сортировки?

14. Объясните алгоритм сортировки методом выбора (метод поиска максимального или минимального элемента).

Лабораторная работа № 5 Двумерные массивы

Цель работы – освоить работу с матрицами, научиться организовывать циклы для обработки многомерных массивов.

Постановка задачи

Написать две программы согласно индивидуальному варианту. Ввод элементов матрицы осуществлять с клавиатуры. Во время отладки и тестирования программы размер матрицы можно уменьшить. При выводе матрицы следить за тем, чтобы ее столбцы были выровнены. На экран вывести исходные данные и результат. Использовать форматный вывод.

Варианты заданий

1. Сформировать целочисленную матрицу А размером 7×8, состоящую из 0 и 1 по следующему правилу: если сумма индексов элемента четная, элемент будет нулевым, если нечетная – единичным.

2. Дана вещественная матрица X размера 6×8. В каждом столбце найти наибольшее значение и сформировать одномерный массив из найденных значений.

1. В заданной целочисленной квадратной матрице Y порядка n (n<=8) определить номера строк, все элементы которых четны.

2. Даны вещественная матрица Z размером 8×10 и число X. Поменять местами минимальный элемент матрицы и элемент, значение которого равно заданному X. Если указанный элемент в матрице отсутствует, вывести сообщение об этом.

1. Дана целочисленная квадратная матрица Y порядка n (n<=8). Вычислить среднее арифметическое отрицательных элементов, расположенных на главной и побочной диагоналях.

2. Дана вещественная матрица Z размером 10×12. В каждом ее столбце найти наибольшее и наименьшее значения и сформировать вектор, состоящий из сумм наибольшего и наименьшего элементов каждого столбца.

1. Дана вещественная матрица С размером 6×6, все элементы которой различны. Найти скалярное произведение строки с наибольшим элементом и столбца с наименьшим элементом, т.е. вычислить 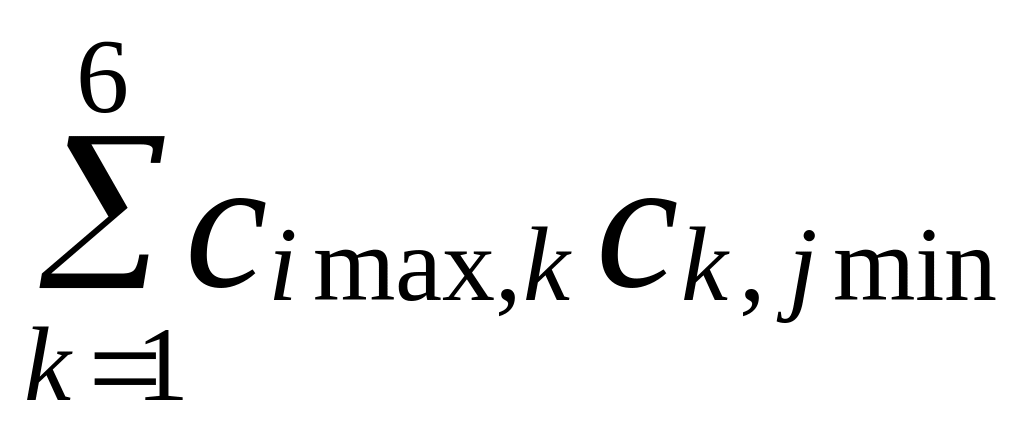, где imax – номер строки с наибольшим элементом, jmin – номер столбца с минимальным элементом.

2. Дана целочисленная матрица R размером 7×8. В каждом ее столбце определить количество четных положительных зна-чений и сформировать из найденных количеств одномерный массив D.

1. Дана целочисленная матрица X размером 10×10. Среди элементов, расположенных выше главной диагонали, найти наибольшее значение.

2. Дана вещественная матрица А размером 6×8. Добавить к ней столбец, состоящий из средних арифметических положительных значений строк матрицы.

1. Дана целочисленная матрица X размером 10×12. Сформировать вектор, каждый элемент которого равен первому четному элементу соответствующего столбца; если четных элементов в столбце нет, присвоить 0.

2. В заданной вещественной матрице B размером 7×8 удалить строку, содержащую наибольшее количество положительных значений.

1. Дана вещественная матрицы А размером 6×8. Сформировать одномерный массив В, состоящий из отрицательных значений матрицы в порядке следования по столбцам.

2. Для целочисленной матрицы А размером 10×10 определить среднее арифметическое значение элементов, лежащих ниже главной диагонали.

1. Дана вещественная матрица М размером 7×8. Преобразовать матрицу, поэлементно вычитая последнюю строку из всех строк, кроме последней.

2. Дана целочисленная матрица В размером 6×6. Вывести номера столбцов, элементы которых образуют возрастающую последовательность.

1. В заданной целочисленной матрице A размером m×n (m,n<=8) определить количество строк, состоящих только из нулей.

2. Дана матрица В размером 7×7. Преобразовать ее так, чтобы минимальные элементы строк оказались на главной диаго- нали.

1. Дана квадратная матрица А размером n×n (n<=6). Определить, является ли она симметричной относительно главной диагонали.

2. Дана вещественная матрица C размером 7×8. В каждой строке определить количество элементов, бóльших среднего арифметического этой строки.

1. Дана вещественная матрица D размером 7×9. Упорядочить ее строки по возрастанию, используя метод попарно-обменной сортировки.

2. Сформировать одномерный массив, каждый элемент которого равен количеству отрицательных элементов соответствующего столбца заданной целочисленной матрицы А размером 5×8.

1. Дана вещественная матрица D размером 7×9. Упорядочить ее столбцы по убыванию, используя метод выбора (поиском максимума).

2. Определить, сколько строк в заданной целочисленной квадратной матрице А порядка n (n<=6) содержат хотя бы один нуль.

1. Дана целочисленная матрица В размером 5×8. Полу- чить массив С из 0 и 1, в котором с_i=1, если в i-й строке матрицы есть хотя бы один отрицательный элемент, и с_i=0 в противном случае.

2. В каждом столбце заданной матрицы D размером 9×10 найти позицию максимального значения и сформировать из них одномерный массив.

1. Дана целочисленная матрица С размером 6×6. Определить количество и сумму элементов, бóльших среднего арифметического элементов матрицы.

2. Дана вещественная матрица D размером 7×9. Преобразовать матрицу, заменив нулем последний отрицательный элемент каждого столбца.

1. В каждой строке заданной вещественной матрицы В размером 9×8 поменять знак у максимального по модулю элемента на противоположный.

2. В каждом столбце матрицы В размером 6×8 найти номер элемента, наиболее близкого к среднему значению этого столбца.

1. В каждой строке матрицы А размером 7×9 поменять местами первый элемент и максимальный по модулю.

2. Дана вещественная матрица D размером 10×12. Выяснить, имеются ли в матрице нулевые элементы. Если имеются, то вывести их индексы; если нет, то вывести сообщение об этом.

1. Дана вещественная квадратная матрица D порядка n (n<=10). В строках с отрицательным элементом на главной диагонали найти сумму элементов.

2. В заданной целочисленной матрице А размером 6×9 поменять местами столбец с наибольшим элементом со столбцом с наименьшим элементом (элементы не повторяются).

1. Дана вещественная матрица C размером 7×8. Удалить из нее строку с наибольшим количеством положительных эле- ментов.

2. В каждой строке матрицы В размером 6×6 найти сумму элементов, больших заданного значения Z.

1. Дана матрица Х размером 5×7 и массив Y из 7 элементов. Поэлементно вычесть массив Y из каждой строки матрицы.

2. Вычислить среднее арифметическое значение максимального и минимального элементов матрицы А размером 9×9, лежащих на побочной диагонали.

1. Дана матрица А размером 4×6. Вывести номера строк, состоящих только из положительных значений, если таких нет, вывести сообщение об этом.

2. Дана вещественная матрица C размером 5×5. Поменять местами максимальный и минимальный элементы побочной диагонали.

1. Дана матрица А размером n×m (n<=7, m<=8) и массив С из n элементов. Заменить столбец матрицы с наименьшей суммой модулей элементов массивом С.

2. Даны натуральное число n, вещественное число X и мат-рица Y размером n×n (n<=10). Получить вектор B, каждый эле-мент которого состоит из 1 и 0. Элемент b_i=1, если все элементы i-й строки матрицы не превосходят X, и b_i=0 в противном слу- чае.

1. Определить седловые точки матрицы М размером 7×8. Седловая точка – элемент, являющийся одновременно максимальным в своей строке и минимальным в своем столбце.

2. Дана целочисленная матрица Y размером n×n (n<=8). Проверить, является ли заданная матрица латинским квадратом (каждая строка и каждый столбец содержат все числа от 1 до n).