
- •Общие положения
- •Лабораторная работа № 1 Структура программы на языке Паскаль. Программирование линейных алгоритмов
- •Постановка задачи
- •Последовательность действий
- •Варианты заданий
- •Контрольные вопросы
- •Лабораторная работа № 2 Программирование ветвлений
- •Постановка задачи
- •Варианты заданий
- •Контрольные вопросы
- •Лабораторная работа № 3 Программирование циклов
- •Постановка задачи
- •Варианты заданий
- •Контрольные вопросы
- •Лабораторная работа № 4 Одномерные массивы
- •Постановка задачи
- •Варианты заданий
- •Контрольные вопросы
- •Лабораторная работа № 5 Двумерные массивы
- •Постановка задачи
- •Варианты заданий
- •Контрольные вопросы
- •Лабораторная работа № 6 Подпрограммы
- •Постановка задачи
- •Варианты заданий
- •Контрольные вопросы
- •Лабораторная работа № 7 Строки
- •Постановка задачи
- •Варианты заданий
- •Контрольные вопросы
- •Лабораторная работа № 8 Тип данных «запись». Массив записей
- •Постановка задачи
- •Варианты заданий
- •Контрольные вопросы
- •Библиографический список
- •Образец оформления отчета
- •Блок-схема
- •Листинг программы
- •Результаты работы программы
- •Основы программирования на языке Паскаль
- •190005, С.-Петербург, 1-я Красноармейская ул., д.1
Контрольные вопросы
Каков синтаксис условного оператора?
Каков тип выражения, определяющего условие в условном операторе?
Какие операции относятся к операциям отношения, какие к логическим операциям?
Какие логические операции Вы знаете? Объясните их смысл и укажите их приоритеты.
Какие значения может принимать логическая переменная? Какие операции к ней применимы?
Можно ли вводить и выводить данные логического типа?
Почему при записи составного условия простые условия (отношения) должны заключаться в скобки?
Какие операции имеют самый высокий приоритет: арифметические, логические или операции отношения? У каких операций самый низкий приоритет?
Почему логический тип относится к порядковым?
Может ли логическое выражение содержать несколько операций? Какие операции могут в нем использоваться?
Как работает условный оператор?
Что такое составной оператор? Для чего он используется?
Что представляет собой вложенный условный оператор? Каковы особенности его использования?
Для чего применяется оператор выбора? Каков его синтаксис?
Как будет выглядеть условный оператор, заменяющий оператор выбора?
Лабораторная работа № 3 Программирование циклов
Цель работы – научиться различать арифметические и итерационные циклы и реализовывать циклические алгоритмы с помощью операторов цикла for, while и repeat.
Постановка задачи
Написать четыре программы согласно индивидуальному варианту. В первой программе смоделировать арифметический цикл с помощью оператора цикла for. Во второй программе использовать циклы while или repeat. В третьей программе вычислить бесконечную сумму с заданной точностью, используя рекуррентные зависимости, в четвертой – использовать при написании программы конструкцию “цикл в цикле”. На экран вывести исходные данные и результат. Использовать форматный вывод. Ни в одной из программ массивы не использовать.
Варианты заданий
Получить таблицу температур по Цельсию от 0 до 100 и их эквивалентов по шкале Фаренгейта, используя для перевода формулу
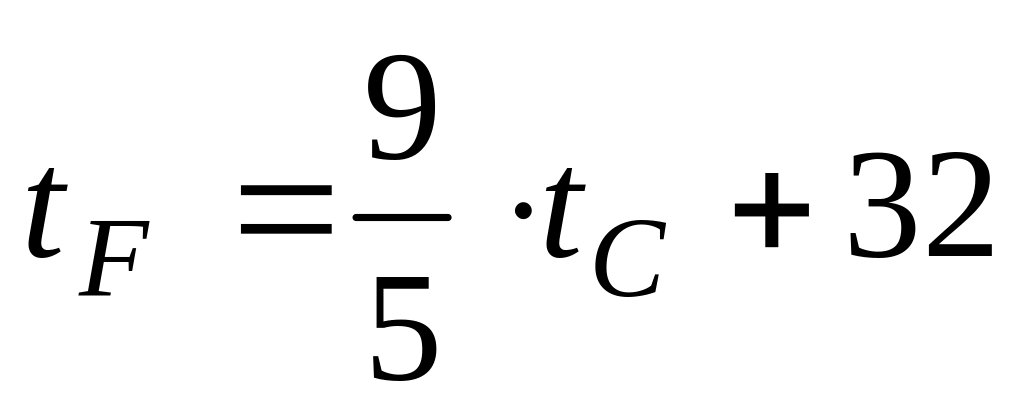 .
.Найти первое число Фибоначчи, большее заданного n (n>1).
Вычислить значение суммы бесконечного ряда с точностью до члена ряда, по модулю меньшего e=10-4,
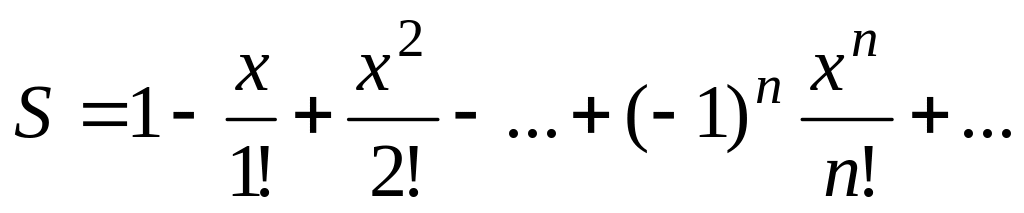 ,
и значение функции (для проверки) f=e-x
. Вывести на экран значение указанной
функции и значение суммы ряда. Оба
значения должны совпадать.
,
и значение функции (для проверки) f=e-x
. Вывести на экран значение указанной
функции и значение суммы ряда. Оба
значения должны совпадать.Дано целое k > 2. Напечатать все простые числа из диапазона [2,k].
Вычислить первые 20 чисел Фибоначчи Fn=Fn-1+Fn-2, F0=F1=1.
Пусть последовательность определяется следующим образом x0=1,
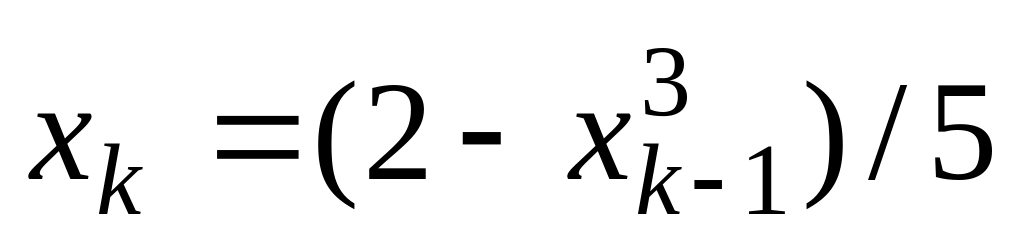 ,
k=1,2,….
Найти первый член
xn,
для которого выполняется условие
,
k=1,2,….
Найти первый член
xn,
для которого выполняется условие
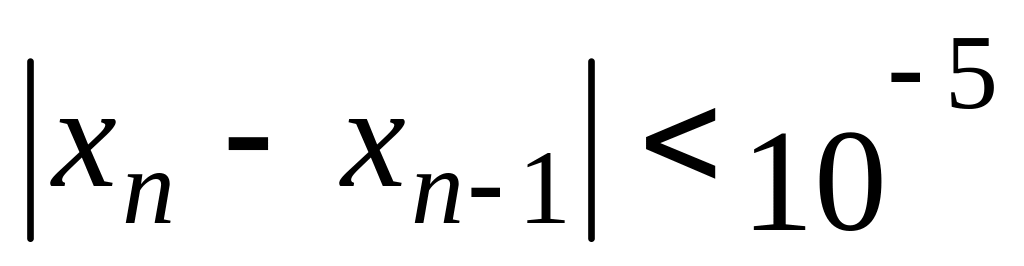 .
.Вычислить значение суммы бесконечного ряда
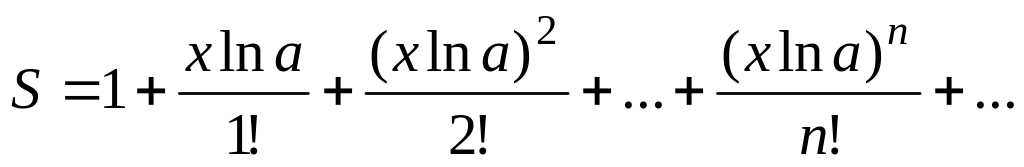 ,
с точностью до члена
ряда, меньшего
e=10-4,
и значение
функции (для проверки)
f=ax;
учесть, что функция определена при 0,1
< = x
< = 1.
Вывес-
ти на экран значение указанной
функции и значение суммы
ряда. Оба
значения должны совпадать.
,
с точностью до члена
ряда, меньшего
e=10-4,
и значение
функции (для проверки)
f=ax;
учесть, что функция определена при 0,1
< = x
< = 1.
Вывес-
ти на экран значение указанной
функции и значение суммы
ряда. Оба
значения должны совпадать.Последовательно вводятся вещественные числа. Признаком окончания ввода является отрицательное число или нуль. Вычислить произведение (Х-2)(Х-4)(Х-6)…(Х-22) для каждого из введенных чисел Х.
Вычислить F=1!+2!+…+n!
Дано натуральное число n. Составить программу для сравнения цифр старшего и младшего разрядов этого числа.
Вычислить значение суммы бесконечного ряда
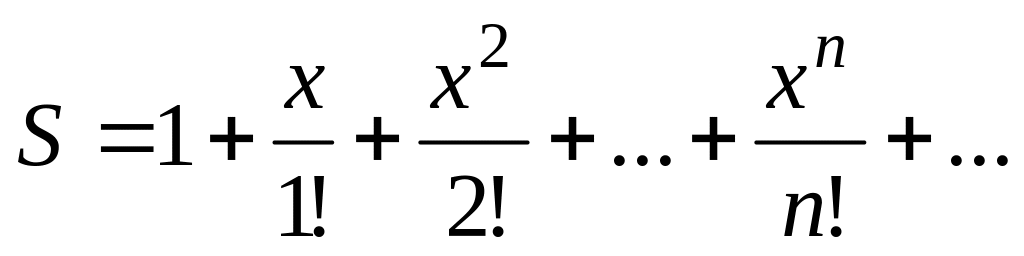 с точностью до члена ряда, по модулю
меньшего e=10-3,
и значение функции (для проверки) f=ex
; учесть, что функция определена при 1
< = x<
= 2. Вывести на экран значение указанной
функции и значение суммы ряда. Оба
значения должны совпадать.
с точностью до члена ряда, по модулю
меньшего e=10-3,
и значение функции (для проверки) f=ex
; учесть, что функция определена при 1
< = x<
= 2. Вывести на экран значение указанной
функции и значение суммы ряда. Оба
значения должны совпадать.Последовательно вводятся числа a (до тех пор, пока не будет введен 0). Для каждого из них вычислить значение функции y=sinx+a при х, изменяющемся на отрезке от –
 до
с шагом 0,1.
до
с шагом 0,1.
Дано 20 целых чисел, которые вводятся по одному. Получите сумму тех из них, которые нечетны и отрицательны.
Дано натуральное число n. Составить программу для определения количества цифр в этом числе.
Вычислить значение суммы бесконечного ряда
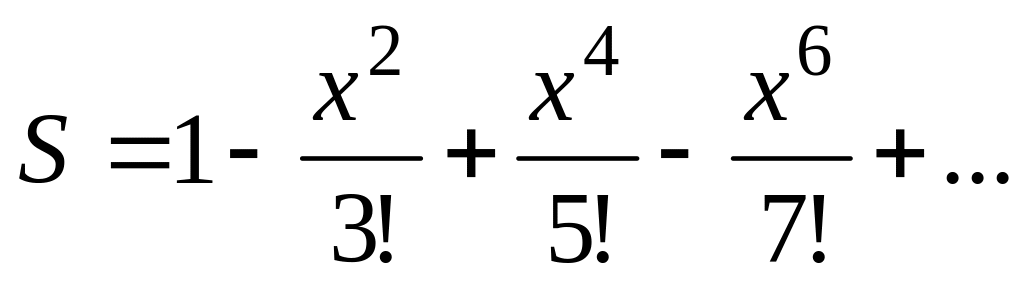 ,
с точностью до члена ряда, по модулю
меньшего e=10-5,
и значение функции (для проверки) f
=
,
с точностью до члена ряда, по модулю
меньшего e=10-5,
и значение функции (для проверки) f
=
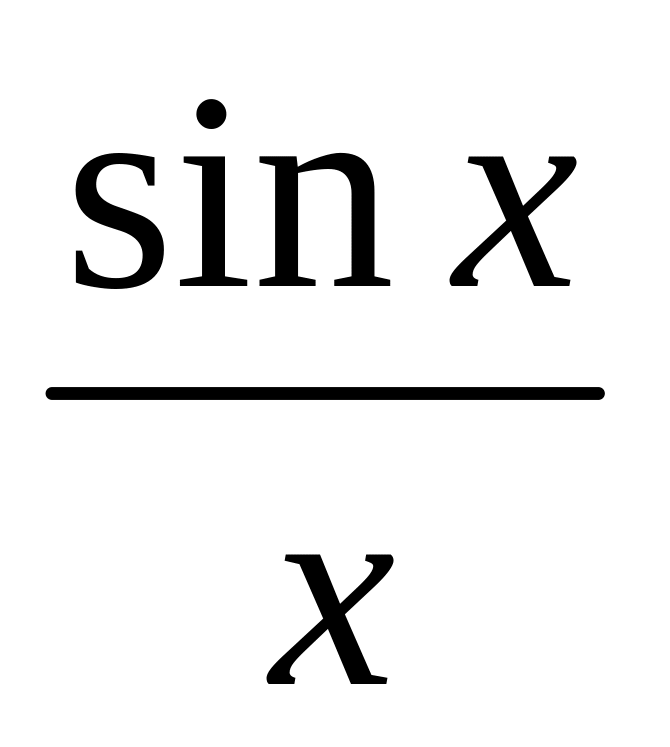 ;
учесть, что -3,14<=
x
<= 3 14.
Вывести на
экран значение указанной функции и
значение суммы ряда. Оба значения должны
совпадать.
;
учесть, что -3,14<=
x
<= 3 14.
Вывести на
экран значение указанной функции и
значение суммы ряда. Оба значения должны
совпадать.Написать программу для поиска N (N вводится) первых простых чисел.
Вычислить a(a-n)(a-2n)…(a-n2). Вещественное а и целое n вводятся с клавиатуры.
Вычислить за сколько лет в банке «Сибнефть» при начальном вкладе W и процентах годового прироста Pr будет накоплена сумма Sum.
Вычислить значение суммы бесконечного ряда с заданной точностью e=10-3,
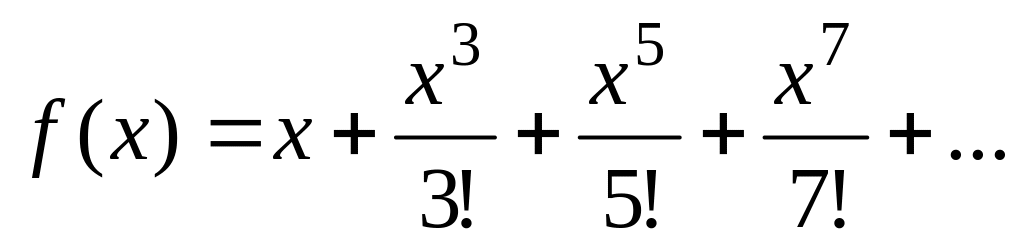 ,
и значение функции (для проверки)
,
и значение функции (для проверки)
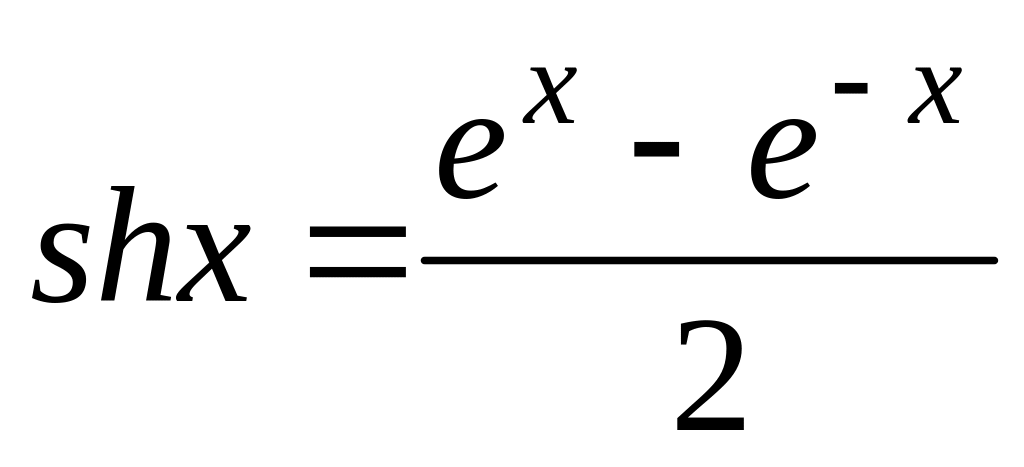 .
Вывести на экран значение указанной
функции и значение суммы ряда. Оба
значения должны совпадать.
.
Вывести на экран значение указанной
функции и значение суммы ряда. Оба
значения должны совпадать.Последовательно вводятся n натуральных чисел (n <=10). Вычислить сумму тех из них, у которых первая цифра равна последней.
Последовательно вводятся n действительных чисел (n<=20). Вычислить среднее арифметическое этих чисел.
Составить программу для определения, является ли натуральное число k степенью числа 3 (операцию возведения в степень не использовать).
Вычислить значение суммы бесконечного ряда с заданной точностью e=10-5 s=
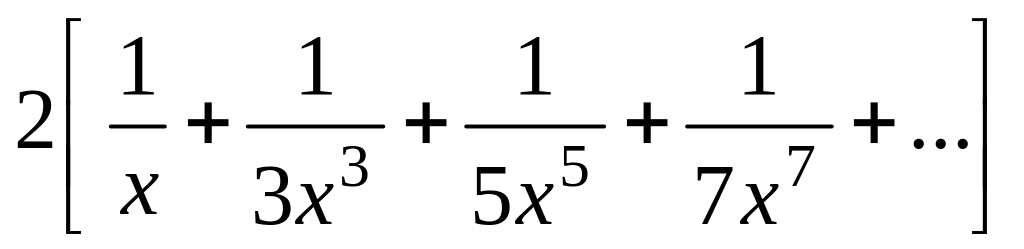 и значение функции (для проверки)
и значение функции (для проверки)
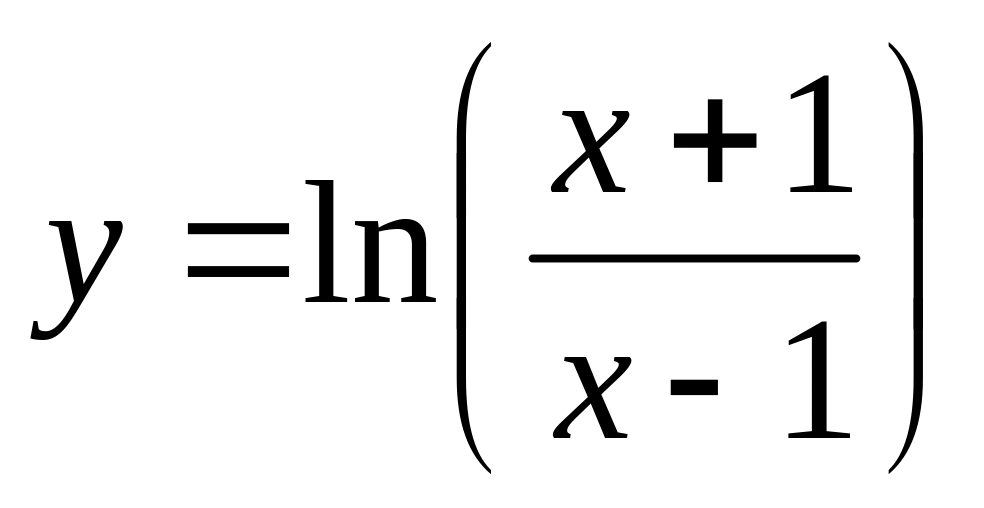 ;
учесть, что функция определена при
x2>1.
Вывести на экран значение указанной
функции и значение суммы ряда. Оба
значения должны совпадать.
;
учесть, что функция определена при
x2>1.
Вывести на экран значение указанной
функции и значение суммы ряда. Оба
значения должны совпадать.Для каждого из n (n≤10) значений переменной х, изменяющейся от –b до b с постоянным шагом, вычислить значение произведения Р=х*(х+0,2)*(х+0,4)*…*(х+1,8).
Вывести таблицу значений функции у=2sinx+cos2x на отрезке от a = - до b = для значений аргумента xi=a+ih, i=0,1,2,…n; h=
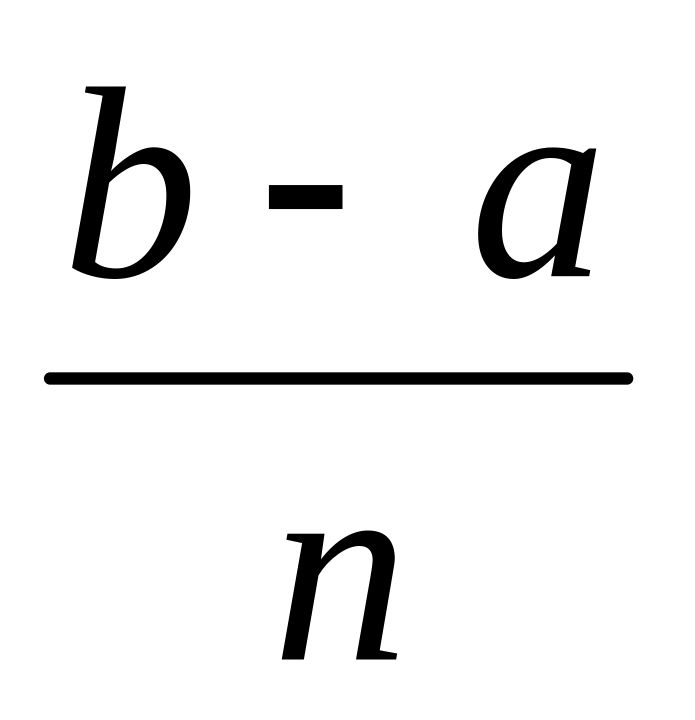 ;
n=10.
;
n=10.Дано целое m >1. Получить наибольшее целое k, при котором 4k < m.
Вычислить значение суммы бесконечного ряда
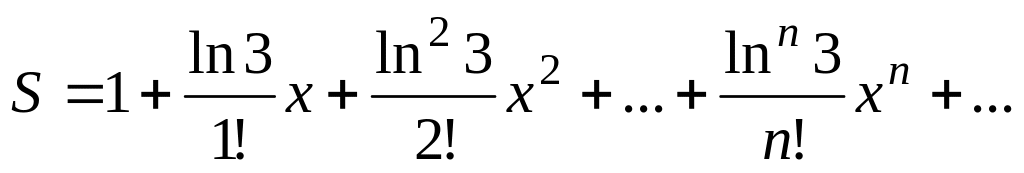 ,
с точностью до члена ряда, по модулю
меньшего e=10-4
, и значение функции (для проверки) f=3x,
учесть, что функция определена при
0<= x <=1.
Вывести на экран значение указанной
функции и значение суммы ряда. Оба
значения должны совпадать.
,
с точностью до члена ряда, по модулю
меньшего e=10-4
, и значение функции (для проверки) f=3x,
учесть, что функция определена при
0<= x <=1.
Вывести на экран значение указанной
функции и значение суммы ряда. Оба
значения должны совпадать.Дано k натуральных чисел. Определить, сколько из них совершенных. Совершенным называется число, равное сумме всех своих делителей, включая 1 и не включая само число.
Последовательно вводятся n (n≤10) целых чисел. Получить сумму тех чисел, которые принадлежат заданному интервалу (а,b).
Дано натуральное n. Составить программу для поиска первой цифры этого числа.
Вычислить значение суммы бесконечного ряда с заданной точностью e=10-4
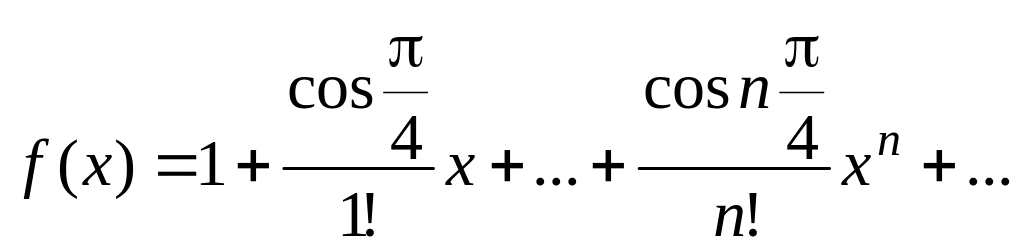 ,
и значение функции (для проверки)
,
и значение функции (для проверки)
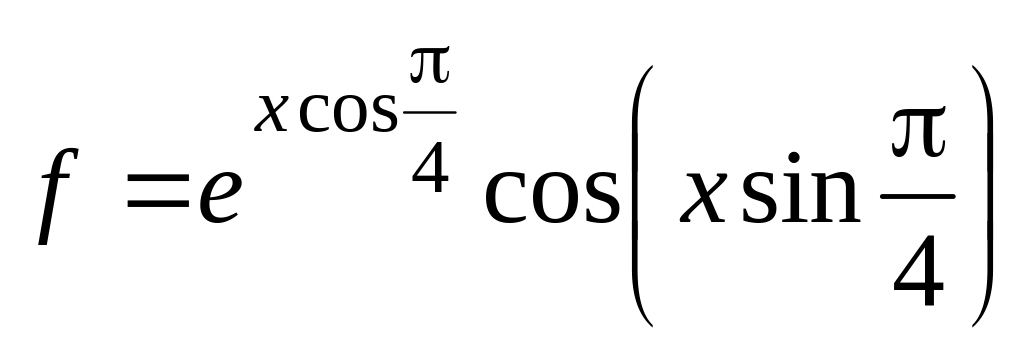 ;
учесть, что функция определена при
;
учесть, что функция определена при
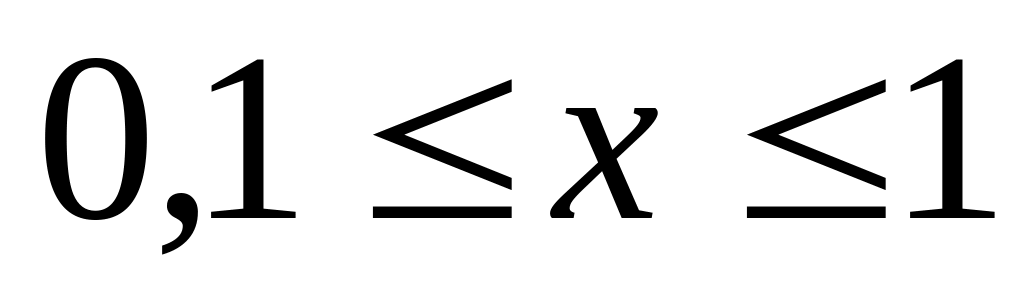 .
Вывести на экран значение указанной
функции и значение суммы ряда. Оба
значения должны совпадать.
.
Вывести на экран значение указанной
функции и значение суммы ряда. Оба
значения должны совпадать.Последовательно вводятся целые положительные числа. Для каждого числа выяснить, является ли оно факториалом какого-либо числа. Если да, то вывести число, факториалом которого является введенное, если нет, вывести сообщение об этом. Признаком конца ввода является ввод нуля.
Вводится последовательность из n целых чисел. Найти максимальное среди них.
Дано натуральное число n. Выяснить, является ли оно степенью числа 5 (операцию возведения в степень не использовать).
Вычислить значение суммы бесконечного ряда с заданной точностью e=10-4
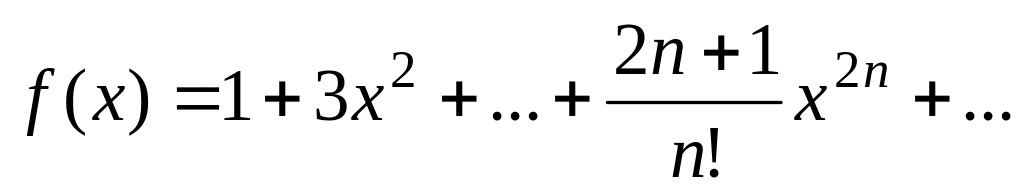 ,
и значение функции (для проверки)
,
и значение функции (для проверки)
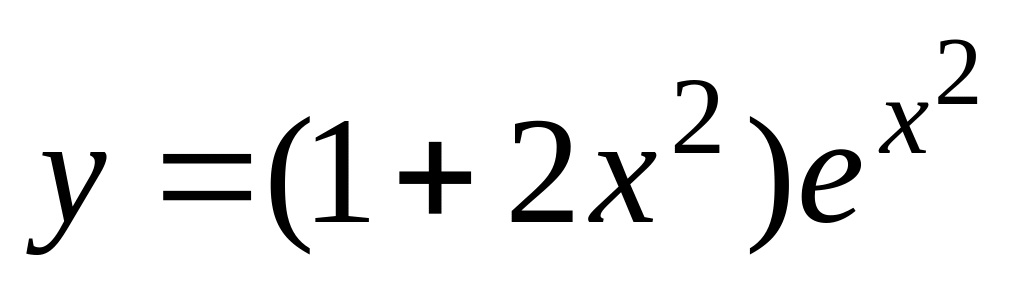 ,
учесть, что функция определена при
.
Вывести на экран значение указанной
функции и значение суммы ряда. Оба
значения должны совпадать.
,
учесть, что функция определена при
.
Вывести на экран значение указанной
функции и значение суммы ряда. Оба
значения должны совпадать.Для каждого из 20 значений переменной x, изменяющейся от -a до a с постоянным шагом, вычислить значение суммы
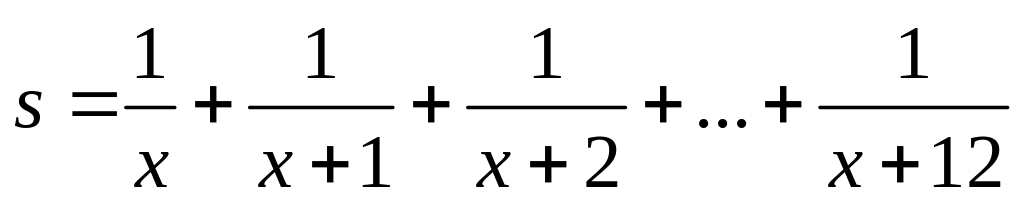 .
.
Даны натуральное число n и вещественное х. Вычислить
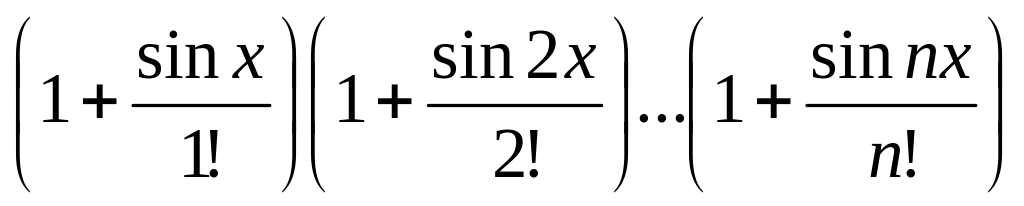 .
.Спортсмен в первый день пробежал 10 км. Каждый следующий день он увеличивал дневную норму на 10% от пробега предыдущего дня. Через сколько дней спортсмен будет пробегать в день больше 20 км?
Вычислить значение суммы бесконечного ряда с заданной точностью e=10-4
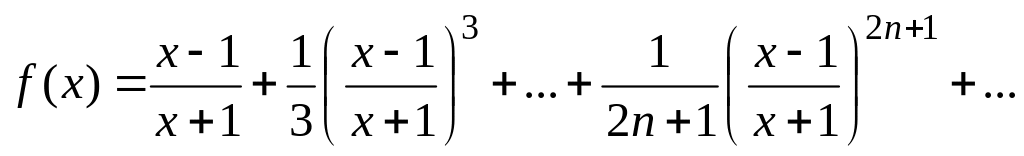 ,
и значение функции (для проверки)
,
и значение функции (для проверки)
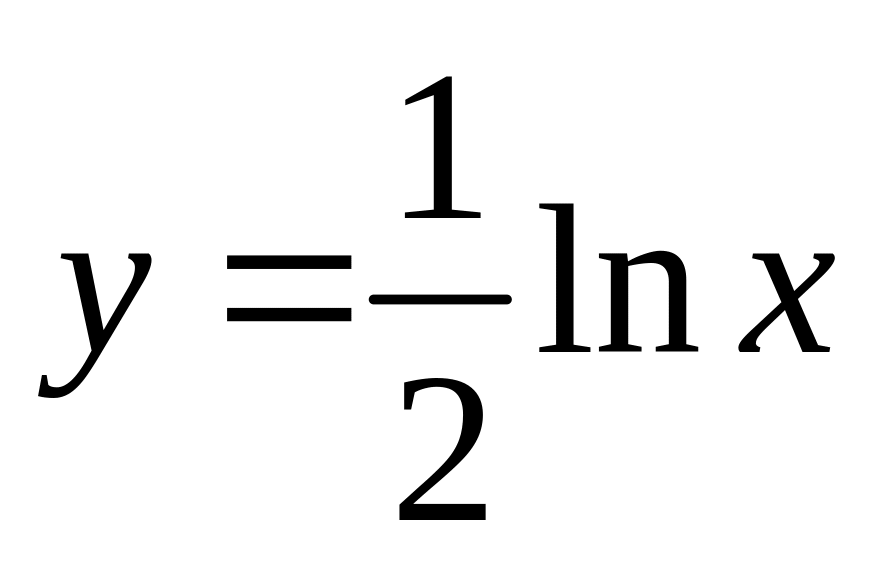 ;
учесть, что функция определена при
;
учесть, что функция определена при
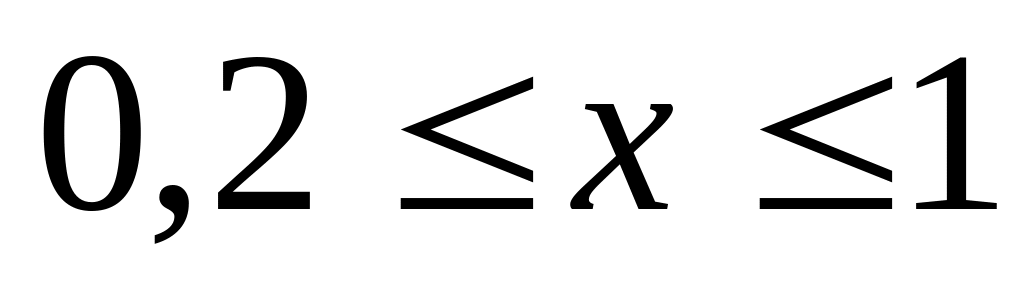 .
Вывести на экран значение указанной
функции и значение суммы ряда. Оба
значения должны совпадать.
.
Вывести на экран значение указанной
функции и значение суммы ряда. Оба
значения должны совпадать.Найти натуральное число в диапазоне от 2 до n (n <=500) с максимальной суммой делителей (само число в сумму не включать).
Даны натуральные числа a и b. Определить все числа, кратные a и b, меньшие a*b (a и b должны быть больше 10).
Факториал некоторого числа равен p. Найти это число.
Вычислить значение суммы бесконечного ряда
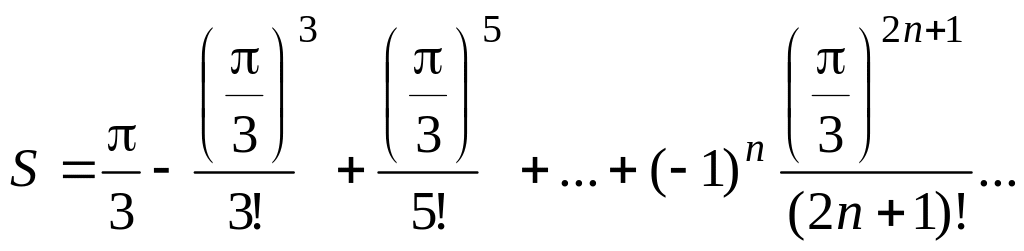 с
заданной точностью e=10-4
и значение функции (для проверки)
f=sin
с
заданной точностью e=10-4
и значение функции (для проверки)
f=sin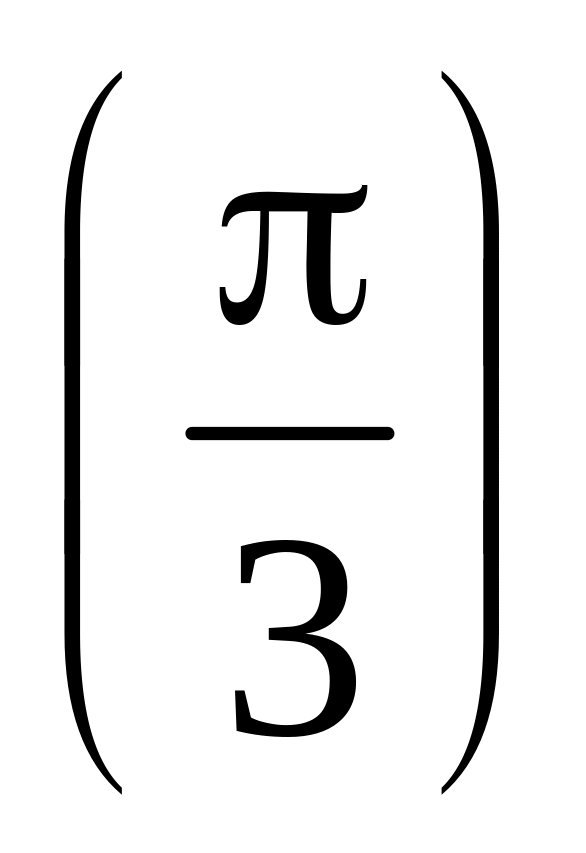 .
. Вывести на экран значение указанной
функции и значение суммы ряда. Оба
значения должны совпадать.
Вывести на экран значение указанной
функции и значение суммы ряда. Оба
значения должны совпадать.Для заданных x=2, 3, 4 ,5, 6, 7, 8, 9, 10 вычислить значение y=
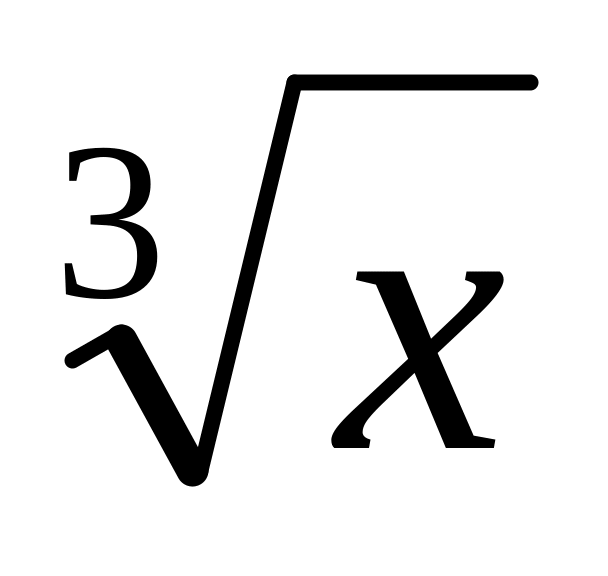 по рекуррентному соотношению Ньютона:
по рекуррентному соотношению Ньютона:
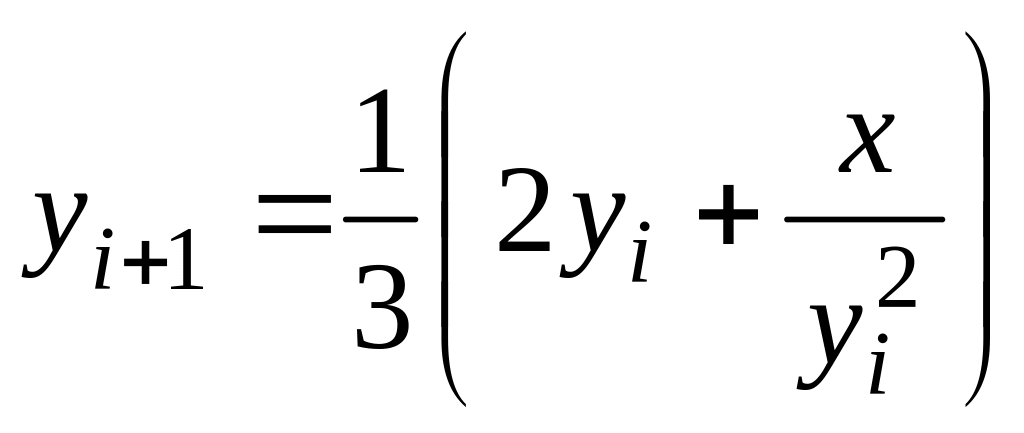 ,
y0=0,3x.
Вычисления продолжать до тех пор, пока
не выполнится условие
,
y0=0,3x.
Вычисления продолжать до тех пор, пока
не выполнится условие
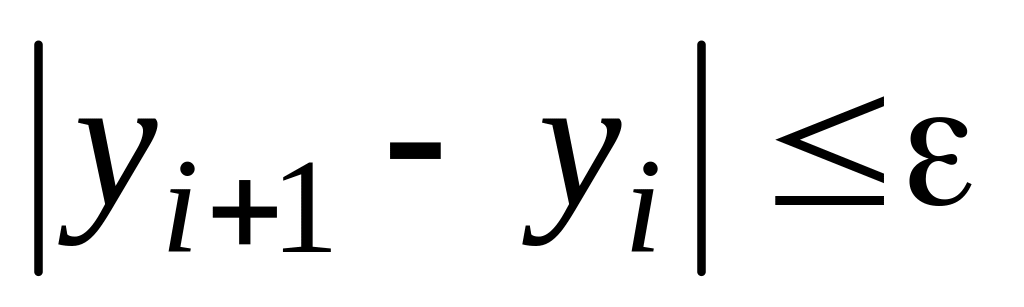 ,
e=10-4.
Подсчитать, сколько итераций надо
выполнить для этого.
,
e=10-4.
Подсчитать, сколько итераций надо
выполнить для этого.
Вычислить и вывести n членов арифметической прогрессии с первым членом а и разностью прогрессии р. Определить их произведение.
Дано действительное а. Вычислить
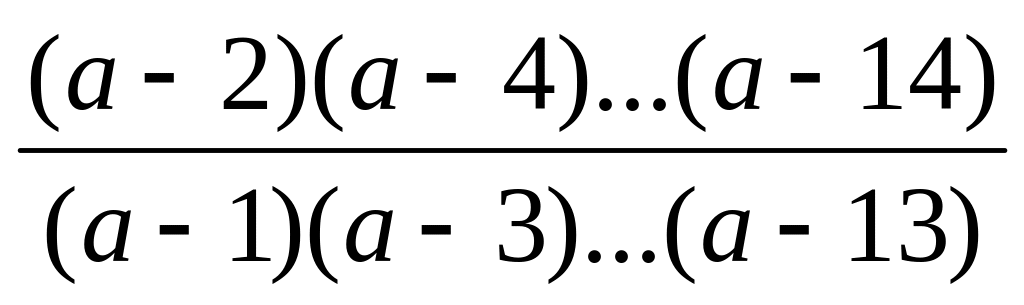 .
.Вычислить значение суммы бесконечного ряда с заданной точностью e=10-4
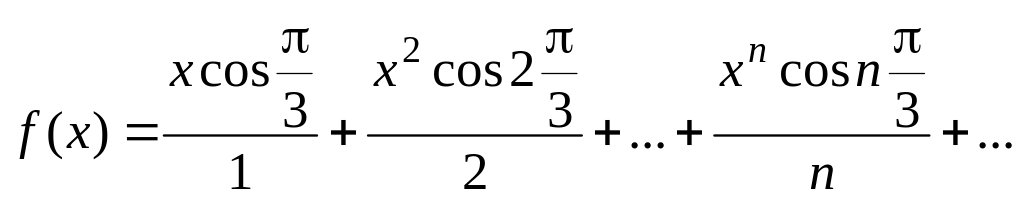 ,
и значение функции (для проверки)
,
и значение функции (для проверки)
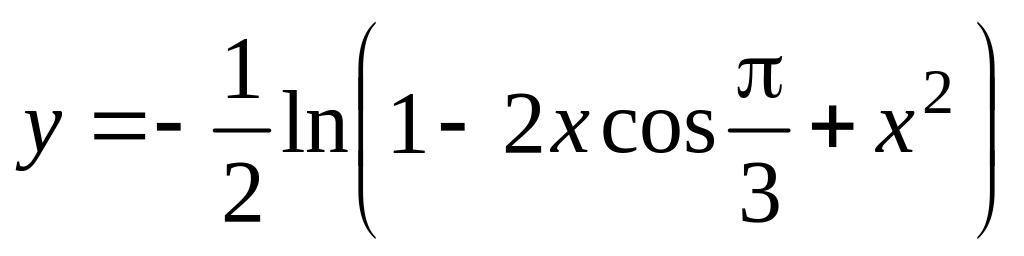 учесть, что функция определена при
учесть, что функция определена при
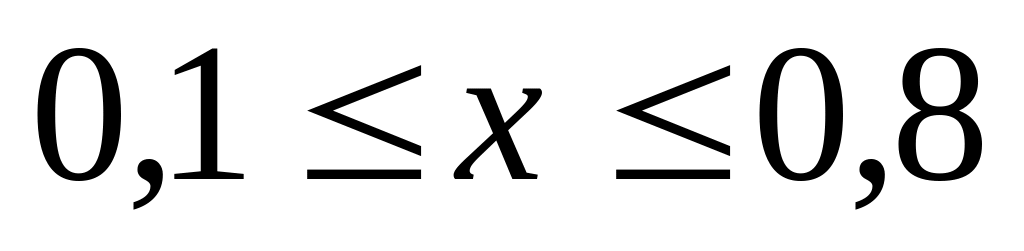 .
Вывести на экран значение указанной
функции и значение суммы ряда. Оба
значения должны совпадать.
.
Вывести на экран значение указанной
функции и значение суммы ряда. Оба
значения должны совпадать.Дано положительное число с. Для каждого значения х=2,3,4,…,7 найти такое наибольшее целое к, при котором хк не превышает заданное с. Операцию возведения в степень не использовать.
Для натурального числа n получить все его натуральные нечетные делители.
Определить наибольшее натуральное число, факториал которого не превышает 105.
Вычислить значение суммы бесконечного ряда с заданной точностью e=10-4
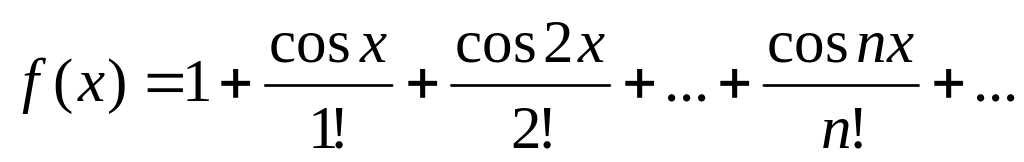 ,
и значение функции (для проверки)
,
и значение функции (для проверки)
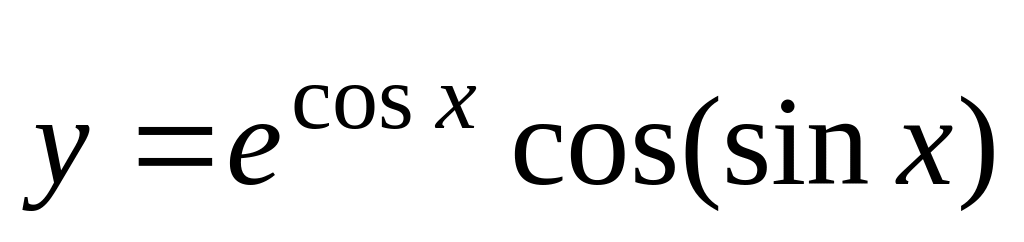 ;
учесть, что функция определена при
;
учесть, что функция определена при
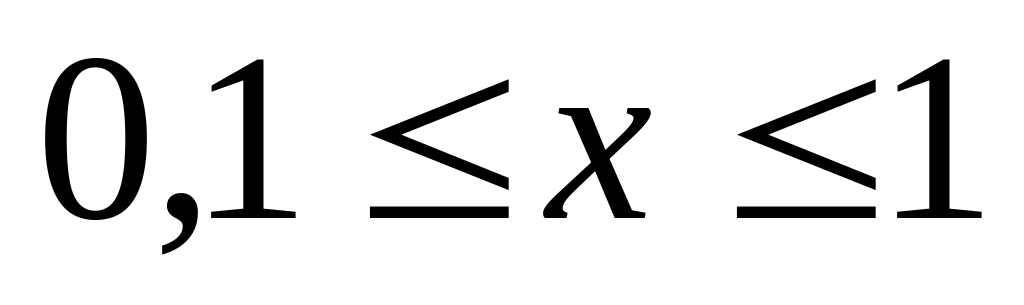 .
Вывести на экран значение указанной
функции и значение суммы ряда. Оба
значения должны совпадать.
.
Вывести на экран значение указанной
функции и значение суммы ряда. Оба
значения должны совпадать.Дано натуральное число n. Вычислить S=1+22+33+…+nn. Операцию возведения в степень не использовать.
Дано 10 вещественных чисел. Определить, образуют ли они возрастающую последовательность.
Последовательно вводятся числа до тех пор, пока не будет введен 0. Найти количество чисел, которые не принадлежат заданному интервалу (а,b).
Вычислить значение суммы бесконечного ряда
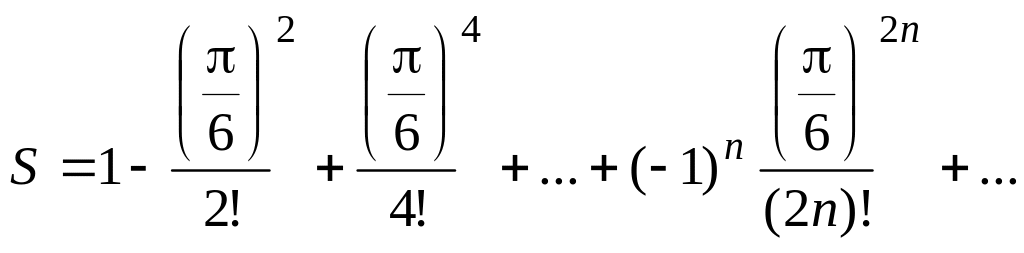 с заданной точностью e=10-4
и значение функции (для проверки)
с заданной точностью e=10-4
и значение функции (для проверки)
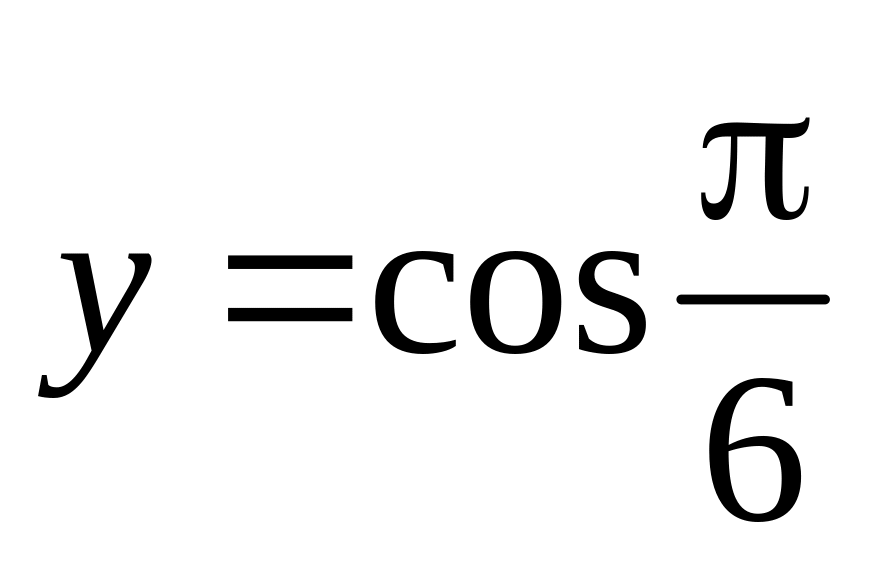 .
Вывести на экран значение указанной
функции и значение суммы ряда. Оба
значения должны совпадать.
.
Вывести на экран значение указанной
функции и значение суммы ряда. Оба
значения должны совпадать.Даны натуральные числа а, b (а<b). Получить все простые числа p, удовлетворяющие неравенству a<p<b.
Дано целое n (n<=30) и вещественное x. Вычислить: y=x + 2x2 +3x3 +…+ nxn.
Вывести на экран значение первого отрицательного члена последовательности cos(ctg(n)), n=1,2,3,…. Отрицательные члены в этой последовательности обязательно есть.
Вычислить значение суммы бесконечного ряда с заданной точностью e=10-5
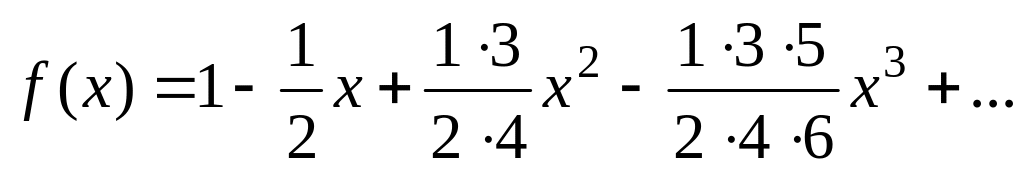 ,
и значение функции (для проверки)
,
и значение функции (для проверки)
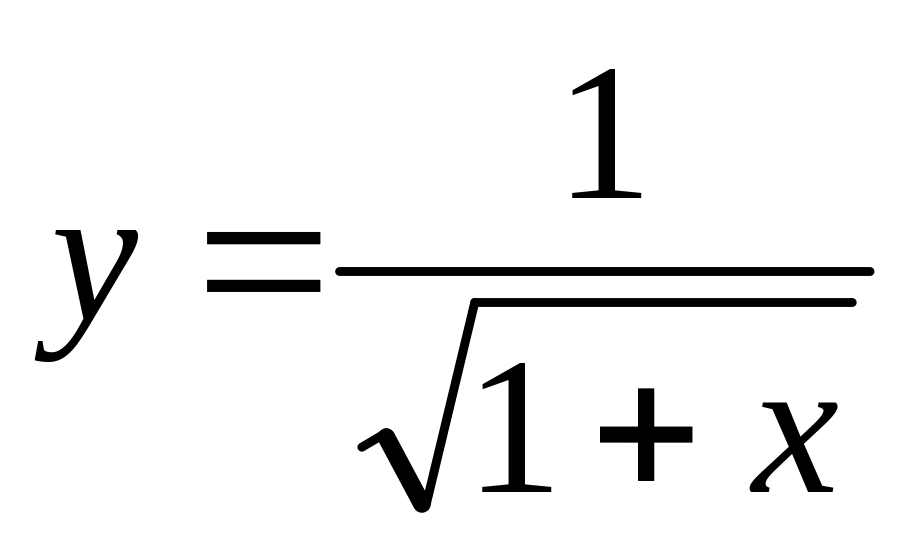 ;
учесть, что функция определена при
x2<1.
Вывести
на экран значение указанной функции и
значение суммы ряда. Оба значения должны
совпадать.
;
учесть, что функция определена при
x2<1.
Вывести
на экран значение указанной функции и
значение суммы ряда. Оба значения должны
совпадать.С клавиатуры вводятся n натуральных чисел (n <=10). Определить сумму цифр для каждого из них.
Последовательно вводятся n натуральных чисел. Вычислить произведение четных из них.
Найти число Фибоначчи, ближайшее к заданному натуральному числу n.
Вычислить значение суммы бесконечного ряда с заданной точностью e=10-3
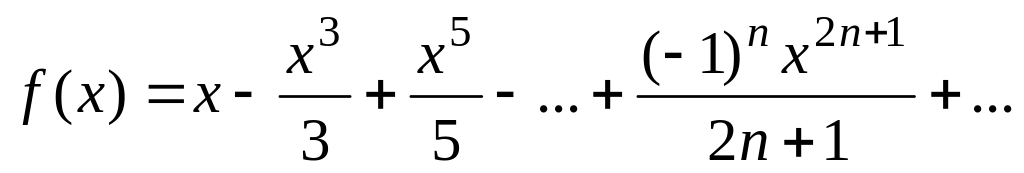 и значение функции (для проверки)
f=arctg(x);
учесть, что
функция определена при x2<1.
Вывести на экран значение указанной
функции и значение суммы ряда. Оба
значения должны совпадать.
и значение функции (для проверки)
f=arctg(x);
учесть, что
функция определена при x2<1.
Вывести на экран значение указанной
функции и значение суммы ряда. Оба
значения должны совпадать.Последовательность a1, a2, a3,... образована по закону а1=b, ai=ai-1-
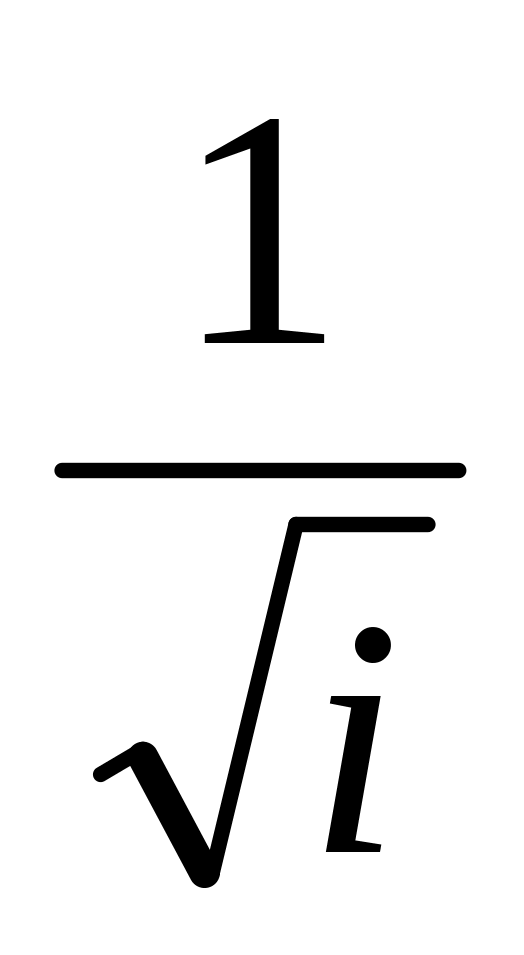 ,
i=2,3,….
Найти первый отрицательный член
последовательности для каждого
b=3,4,5,6,7,8,9.
,
i=2,3,….
Найти первый отрицательный член
последовательности для каждого
b=3,4,5,6,7,8,9.
Дано n(n≤10) вещественных чисел, которые вводятся по одному. Вычислить разность между максимальным и минимальным из них.
Дано натуральное n. Вычислить у=1*3*5*…*n, если n нечетное, и у=2*4*6*…* n, если n четное.
Вычислить значение суммы бесконечного ряда с заданной точностью e=10-4
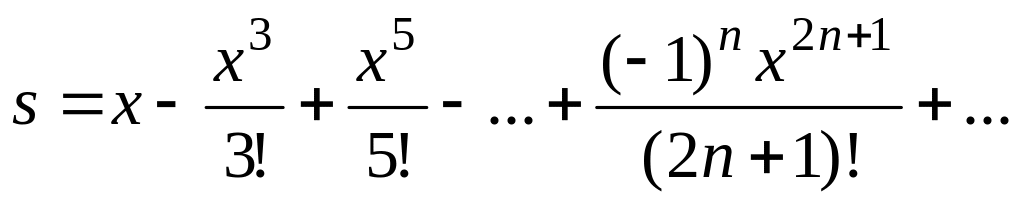 и
значение функции (для проверки)
f(x)=sin(x);
учесть, что функция определена при 0<
и
значение функции (для проверки)
f(x)=sin(x);
учесть, что функция определена при 0<
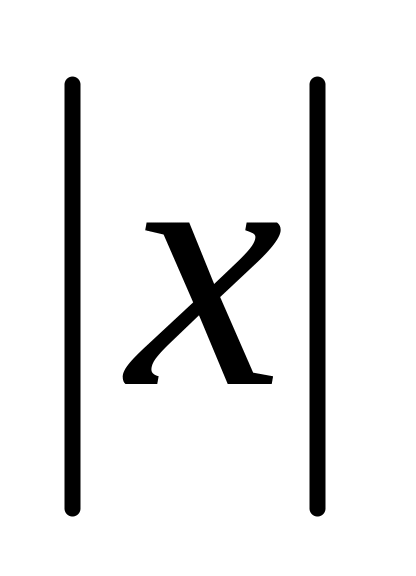 <10.
Вывести на экран значение указанной
функции и значение суммы ряда. Оба
значения должны совпадать.
<10.
Вывести на экран значение указанной
функции и значение суммы ряда. Оба
значения должны совпадать.Дано положительное число k. Для каждого значения x=2,3,4,…,8 найти такое наименьшее целое n, при котором хп превышает заданное k. Операцию возведения в степень не использовать.
У гусей и кроликов вместе 2n лап. Сколько может быть гусей и кроликов? (Вывести все возможные сочетания.)
Последовательно вводятся различные натуральные числа. Признаком окончания ввода является 0. Определить порядковый номер наименьшего из чисел.
Вычислить значение суммы бесконечного ряда с заданной точностью e=10-3
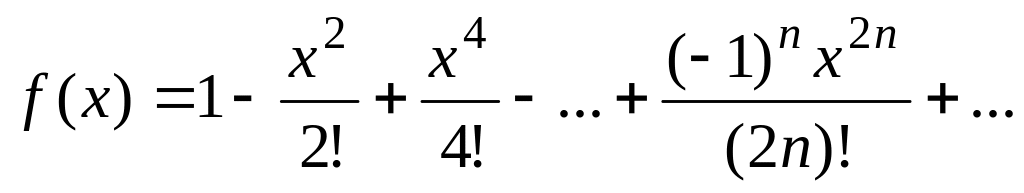 и
значение функции (для проверки)
f(x)=cos(x);
учесть, что функция определена при 0<
<10.
Вывести на экран значение указанной
функции и значение суммы ряда. Оба
значения должны совпадать.
и
значение функции (для проверки)
f(x)=cos(x);
учесть, что функция определена при 0<
<10.
Вывести на экран значение указанной
функции и значение суммы ряда. Оба
значения должны совпадать.Вычислить
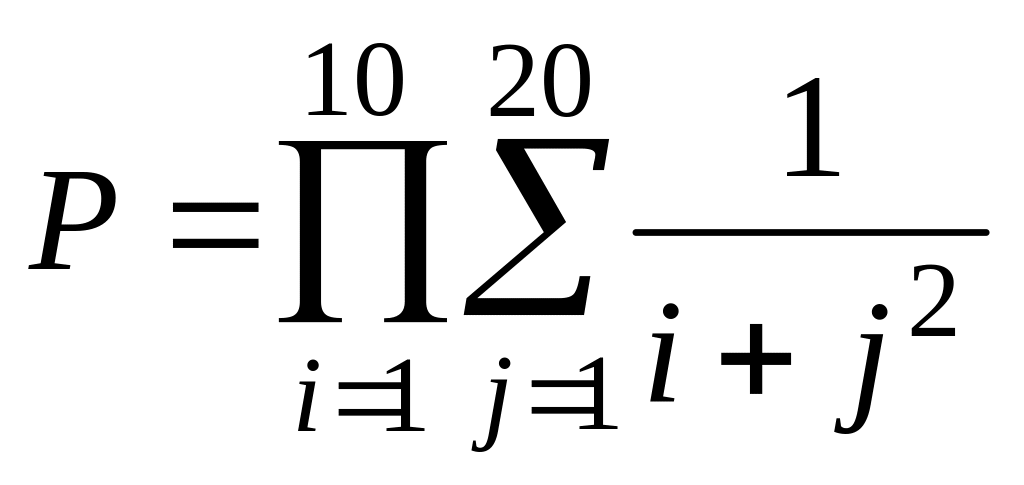 .
.
Вычислить (x2-2!)(x3-3!)(x4-4!)…(xn-n!)
Одноклеточная амеба каждые три часа делится на две клетки. Считая, что первоначально в замкнутом объеме находится 10 клеток, определить, через какое время в этом объеме будет находиться 105 клеток.
Вычислить значение суммы бесконечного ряда с заданной точностью e=10-4
 и значение функции (для проверки)
f = ln(x);
учесть, что
функция определена при x
>1/2. Вывести
на экран значение указанной функции и
значение суммы ряда. Оба значения должны
совпадать.
и значение функции (для проверки)
f = ln(x);
учесть, что
функция определена при x
>1/2. Вывести
на экран значение указанной функции и
значение суммы ряда. Оба значения должны
совпадать.Пользователь вводит n натуральных чисел. Для каждого из них сформировать число, получаемое записью его цифр в обратном порядке.
Для заданного n получить сумму чисел, образованных по закону
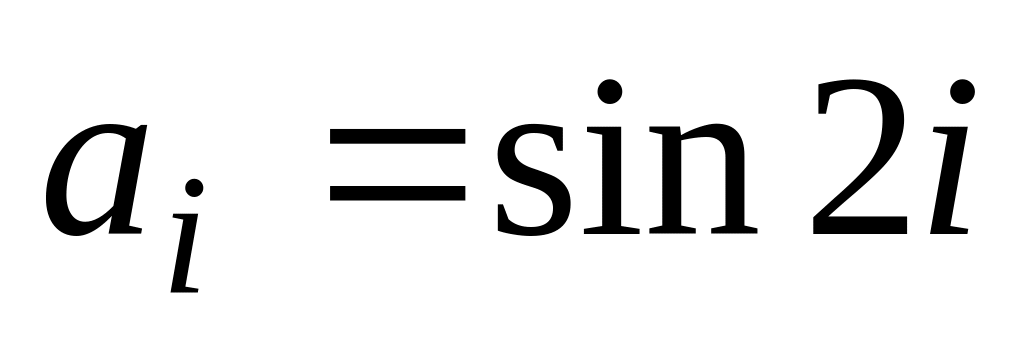 ,
где i=1,
2,…n.
,
где i=1,
2,…n.Вычислить множество значений функции y=x2+b для х, изменяющегося от - a до a с постоянным шагом, равным 0,1, при b=5.
Вычислить значение суммы членов бесконечного ряда
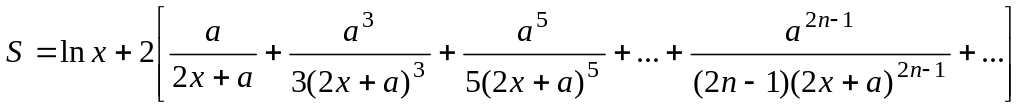 с
точностью до члена ряда, меньшего e=10-4
для
a2<(2x+a)2
и значение
функции (для проверки) f=ln
(x+a).
Вывести на
экран значение указанной функции и
значение суммы ряда. Оба значения должны
совпадать.
с
точностью до члена ряда, меньшего e=10-4
для
a2<(2x+a)2
и значение
функции (для проверки) f=ln
(x+a).
Вывести на
экран значение указанной функции и
значение суммы ряда. Оба значения должны
совпадать.Вычислить s=
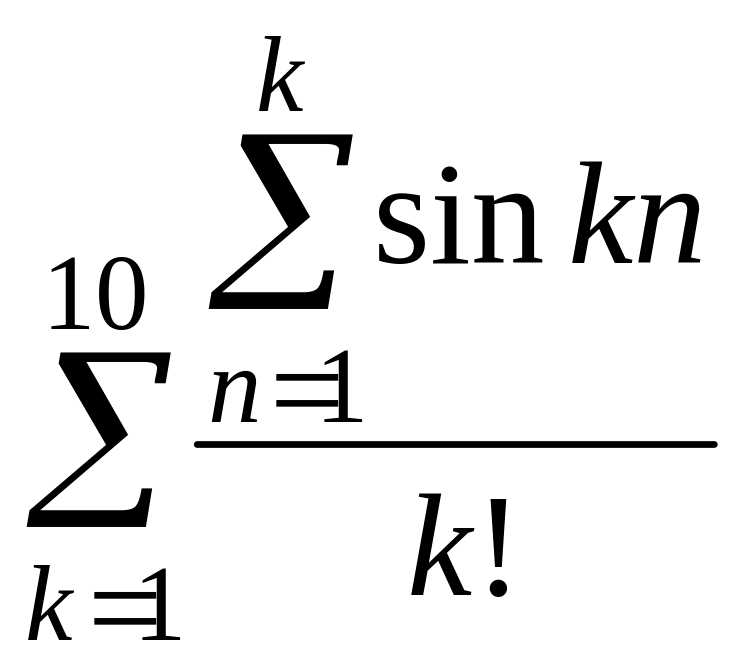 .
.
Определить, являются ли натуральные числа a и b взаимно простыми. Взаимно простые числа не имеют общих делителей, кроме единицы.
Первоначальный объем древесины на участке леса составляет р кубометров. Ежегодный прирост составляет k%. Годовой план заготовки составляет t кубометров. Определить, через сколько лет в этом лесу будут расти одни опята.
Вычислить значение суммы бесконечного ряда
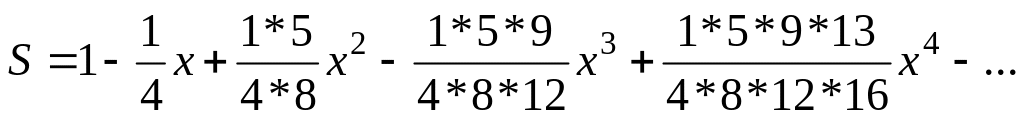 ,
с точностью до члена ряда, по модулю
меньшего e=10-4
, и значение функции (для проверки)
f=(1+x)-1/4;
учесть, что функция определена при
x2<1.
Вывести
на экран значение указанной функции и
значение суммы ряда. Оба значения должны
совпадать.
,
с точностью до члена ряда, по модулю
меньшего e=10-4
, и значение функции (для проверки)
f=(1+x)-1/4;
учесть, что функция определена при
x2<1.
Вывести
на экран значение указанной функции и
значение суммы ряда. Оба значения должны
совпадать.Для каждого из пяти натуральных значений n, вводимых пользователем, вычислить
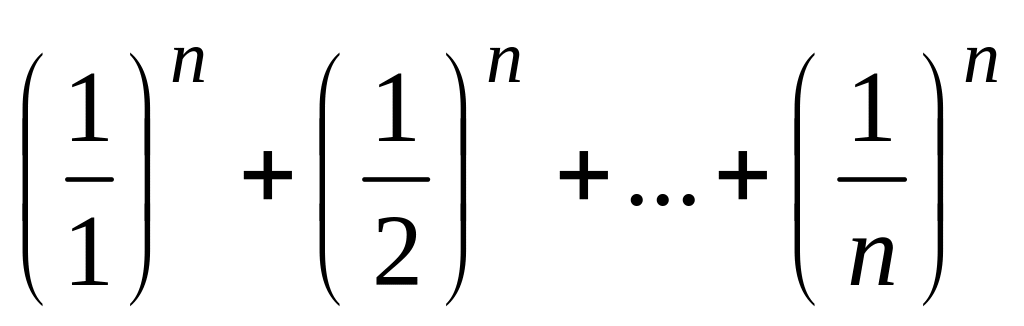 .
.
Дано натуральное число n>10. Составить программу для вычисления значения
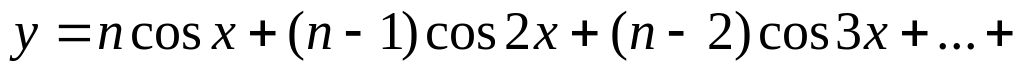 .
.
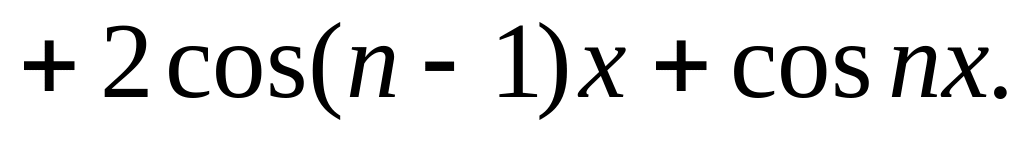
Перевести заданное натуральное число n из десятичной системы счисления в двоичную, т.е. получить число, являющееся двоичной записью исходного числа.
Вычислить значение суммы бесконечного ряда с заданной точностью e=10-4
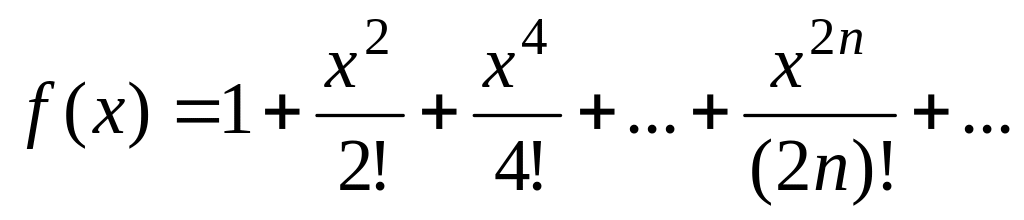 ,
и значение функции (для проверки)
,
и значение функции (для проверки)
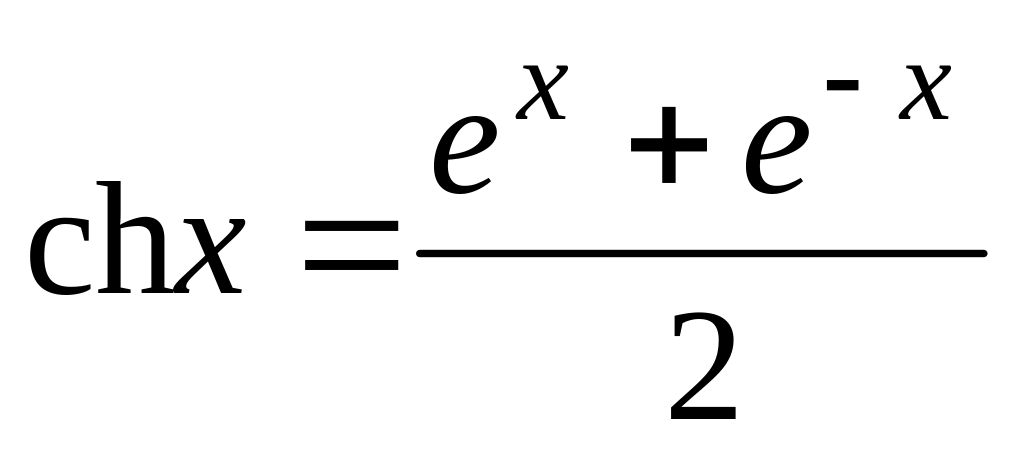 ;
учесть, что функция определена при
0,1<= x <=1.
Вывести на
экран значение указанной функции и
значение суммы ряда. Оба значения должны
совпадать.
;
учесть, что функция определена при
0,1<= x <=1.
Вывести на
экран значение указанной функции и
значение суммы ряда. Оба значения должны
совпадать.Для каждого а=1,2,3,4,5 вычислить и вывести на экран значение функции
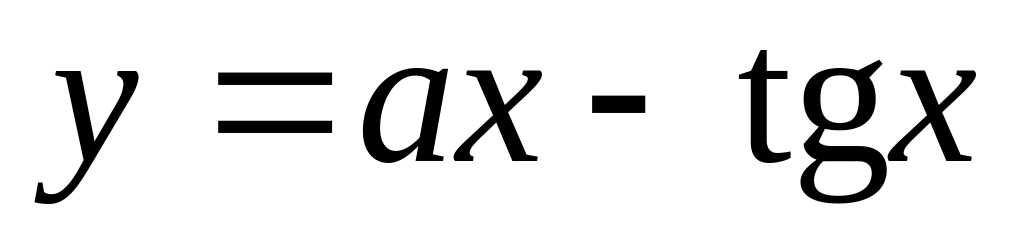 для х=1,1;
1,2;…;1,9.
для х=1,1;
1,2;…;1,9.
