
4. Решение обыкновенных дифференциальных уравнений и систем
В MatLab существует функция ode45, которая реализует метод Рунге-Кутта 4-5 порядка
[X, Y] = ode45('name',[x0 b], y0),
где
name – функция, вычисляющая правую часть уравнения;
[x0 b]– интервал интегрирования дифференциального уравнения;
y0 – начальное условие;
X – массив координат узлов сетки, в которых ищется решение;
Y – массив значений искомой функции в этих узлах.
Как правило, размеры векторов X и Y достаточно велики, поэтому результат лучше отображать на графике.
А) Решение задачи Коши для обыкновенного дифференциального уравнения 1-го порядка:
![]()
Пример.
![]() на отрезке
на отрезке
![]() .
.
Сначала создадим файл-функцию с двумя входными аргументами первым – x (переменной, по которой ведется интегрирование) и вторым – y (искомой функцией) и сохраним под именем fprdif:

Создадим М-файл с именем list_15 для решения ОДУ:

Результатом работы программы будет график

Б) Решение задачи Коши для систем ОДУ:
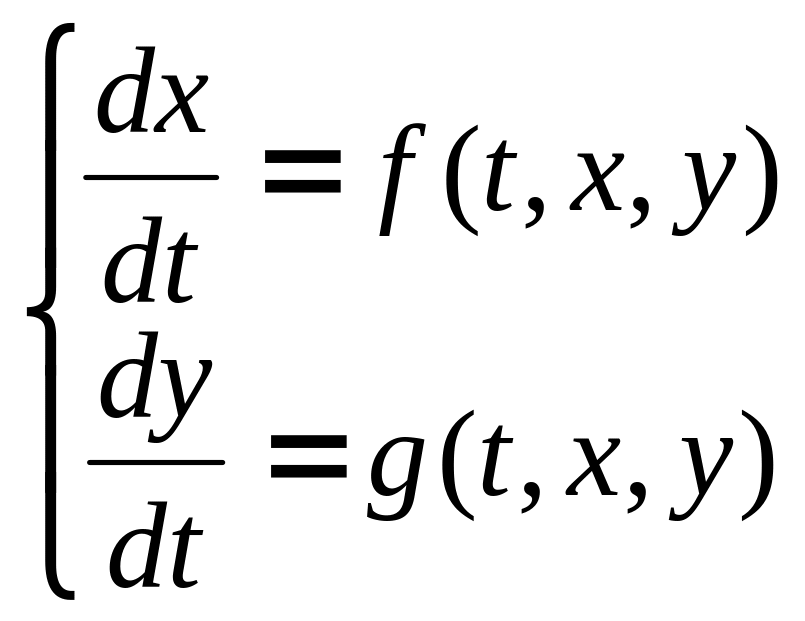 ,
,
![]()
![]() .
.
Пример
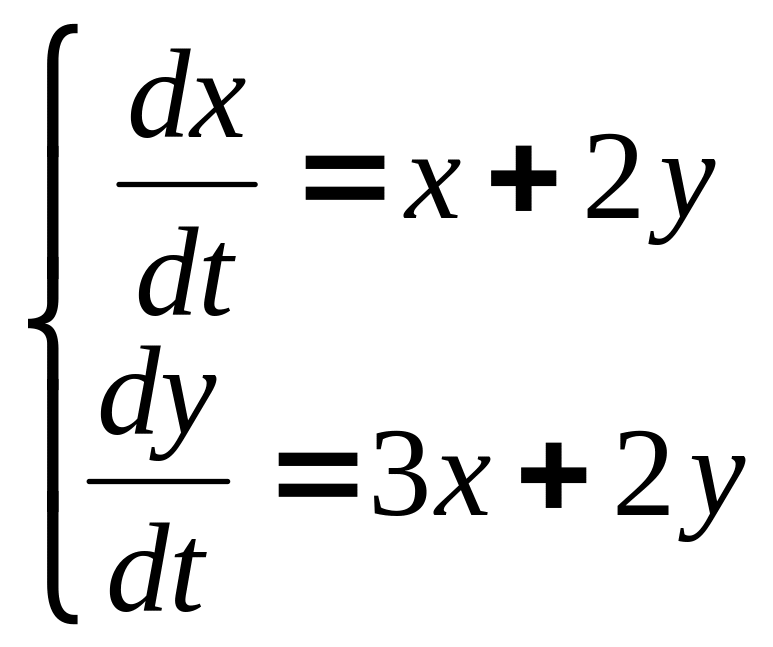 с
с
![]() на интервале
на интервале
![]() .
.
Напишем файл-функцию с двумя входными
аргументами: переменной
![]() ,
по которой ведется дифференцирование,
и вектором
,
по которой ведется дифференцирование,
и вектором
![]() ,
размер которого равен числу неизвестных
функций системы:
,
размер которого равен числу неизвестных
функций системы:
![]() ,
,
![]() .
Выходным аргументом является вектор
правой части системы. Имя функции fosl.
.
Выходным аргументом является вектор
правой части системы. Имя функции fosl.

Далее, обращаемся к функции ode45 в отдельном М-файле list_16.

Результатом работы программы будет график

В) Решение задачи Коши для дифференциальных уравнений высших порядков:
![]()
Алгоритм решения состоит в следующем
Приведение дифференциального уравнения к системе уравнений первого порядка.
Написание специальной файл-функции для правой части системы.
Вызов солвера ode45.
Визуализация результата.
Пример
![]() на отрезке
на отрезке
![]() .
.
Приведем исходное уравнение к системе дифференциальных уравнений. Для этого надо ввести столько вспомогательных функций, каков порядок уравнения. В данном случае введем две вспомогательные функции:
![]() .
.
Тогда получим систему дифференциальных уравнений
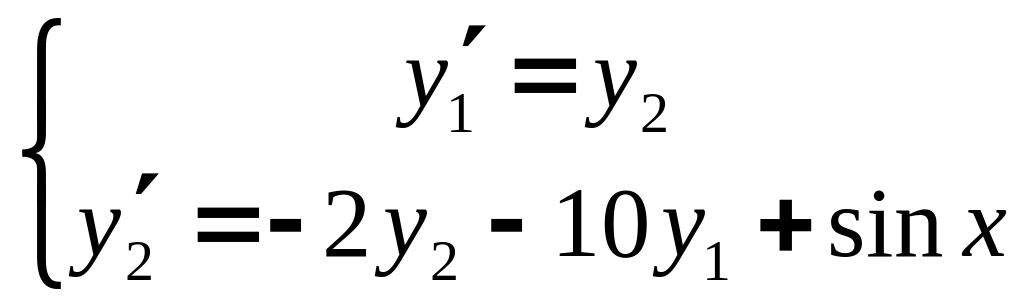
с начальными условиями
![]() .
.
Сначала создаем функцию fosl_1
вычисления правой части системы, в
которой принято обозначение: x
– переменная интегрирования, y
– вектор с элементами
![]() ,
,
![]() :
:

Затем напишем программу list_17 в которой используется солвер ode45 для решения системы соответствующей исходному дифференциальному уравнению:

В результате выполнения программы на экран выводится график приближенного решения

5. Решение краевой задачи
Рассмотрим решение краевой задачи общего вида для обыкновенного дифференциального уравнения второго порядка. Пусть требуется решить уравнение второго порядка
![]()
на отрезке
![]() ,
причем решение должно удовлетворять
следующим условиям на границе отрезка
,
причем решение должно удовлетворять
следующим условиям на границе отрезка
![]() ,
,
где
![]() ,
,
![]()
![]() ,
,
![]() – заданные числа.
– заданные числа.
Решение задачи состоит их нескольких этапов:
Преобразование уравнения второго порядка к системе двух уравнений первого порядка. Для этого вводим две вспомогательные функции:
.
Написание файл-функции для вычисления правой части системы.
Написание файл-функции, определяющей граничные условия. При этом граничные условия требуется записать так, чтобы в правых частях стояли нули:
![]() .
.
Файл-функция должна иметь два входных
аргумента, каждый из которых является
век тором значений неизвестных функций
и
![]() в начальной и конечной точках промежутка.
в начальной и конечной точках промежутка.
Формирование начального приближения при помощи функции bvpinit. Аргументами функции bvpinit являются вектор с координатами узлов сетки и вектор, состоящий из двух элементов, содержащий начальное приближение.
Вызов солвера bvp4c для решения граничной задачи. MatLab находит приближенное решение методом конечных разностей и в результате получается вектор значений функции в точках отрезка (узлах сетки).
Графическое изображение результата.
Пример
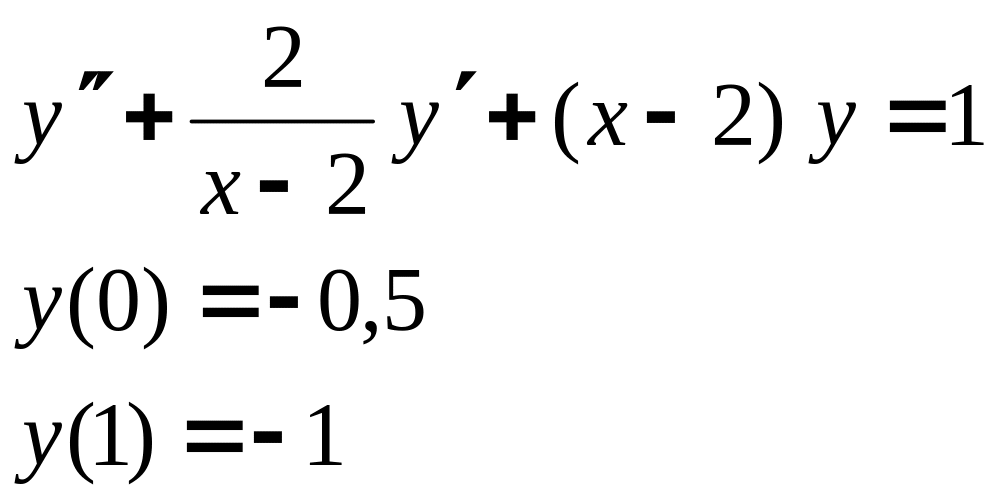 .
.
Здесь
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Введем две вспомогательные функции:
и получим систему дифференциальных уравнений и граничные условия для неё
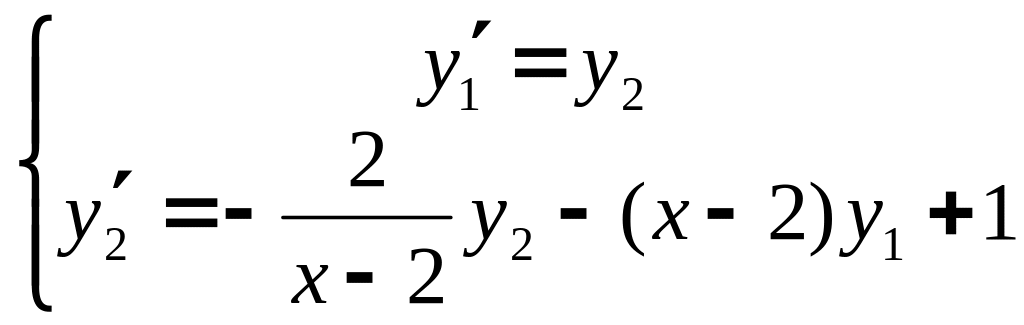
![]() .
.
Напишем файл-функцию rside для правой части системы уравнений:
------------------------------------------------------------------------------------------------------------------------
function f = rside(x, y)
f = [y(2); -2*y(2)./(x-2)-(x-2).*y(1)+1];
------------------------------------------------------------------------------------------------------------------------
Напишем файл-функцию bound для правой части системы уравнений:
------------------------------------------------------------------------------------------------------------------------
function f = bound(ya, yb)
f = [ya(1)+0.5; yb(1)+1];
------------------------------------------------------------------------------------------------------------------------
Решение граничной задачи оформим в виде файл-программы, в которой зададим начальное приближение при помощи bvpinit и вызовем солвер bvp4c для получения приближенного решения, затем построим график приближенного решения в виде множества точек.
------------------------------------------------------------------------------------------------------------------------
% РЕШЕНИЕ КРАЕВОЙ ЗАДАЧИ.
clear all
% ВВОДИМ СЕТКУ С ШАГОМ 0.1:
X0 = [0:0.1:1];
% ФОРМИРУЕМ НАЧАЛЬНОЕ ПРИБЛИЖЕНИЕ:
Y0 = [0 0];
initsol = bvpinit(X0, Y0);
% ВЫЗЫВАЕМ СОЛВЕР BVP4C:
sol = bvp4c('rside', 'bound', initsol);
% CТРУКТУРА sol:
% sol.x – ВЕКТОР, В КОТОРМ СОДЕРЖАТЬСЯ КООРДИНАТЫ УЗЛОВ СЕТКИ
% sol.y – МАТРИЦА, СОСТОЯЩАЯ ИЗ ДВУХ СТРОК,
% sol.y(1, :) – СООТВЕТСТВУЕТ ЗНАЧЕНИЯМ ФУНКЦИИ y1
% sol.y(2, :) - СООТВЕТСТВУЕТ ЗНАЧЕНИЯМ ФУНКЦИИ y2
plot(sol.x, sol.y(1,:), 'r.')
grid on
------------------------------------------------------------------------------------------------------------------------

