Некоторые задачи вычислительной математики

1. Решение задач линейной алгебры.

Пусть A – квадратная матрица.

Для вычисления определителя предназначена встроенная функция det:

D = det(A)

Для нахождения обратной матрицы служит встроенная функция inv:

A1 = inv(A)

Для того чтобы задать в MATLAB систему линейных уравнений необходимо ввести основную матрицу системы и вектор правой части , например, для системы

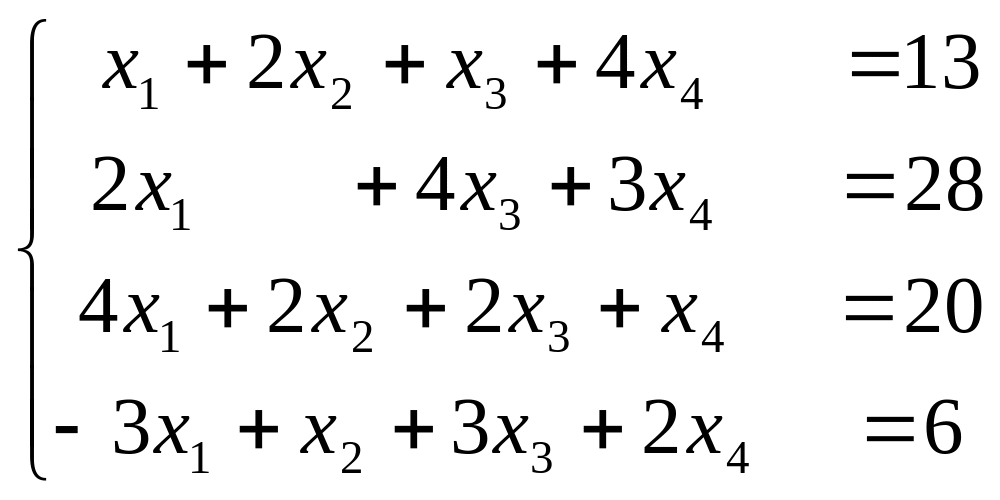
основная матрица системы:

>> A = [1 2 1 4; 2 0 4 3; 4 2 2 1; -3 1 3 2]

вектор правой части:

>> B = [13; 28; 20; 6]

Решение системы линейных алгебраических уравнений в MATLAB можно выполнить при помощи символа \ .

Решение системы:

>> X = A\B

X =

3

-1

4

2

Проверка

>> A *X

В результате должны получить вектор B.

ans =

13.0000

28.0000

20.0000

6.0000

2. Интегрирование функций

Вычисление определенных интегралов

В MatLab существует встроенная функция, реализующая алгоритм метода Симпсона с автоматическим выбором шага

I = quad('имя функции', а, b)

где

имя функции – имя функции, задающей подынтегральное выражение;

а, b – пределы интегрирования,

I – значение интеграла.

Для повышения точности вычислений следует задать дополнительный четвертый аргумент e – точность метода:

I = quad('name', а, b, e).

Например, требуется вычислить определенный интеграл

.

Подынтегральную функцию можно вводить разными способами:

Первый способ.

Создаем файл-функцию, для вычисления подынтегрального выражения и сохраняем её, например, под именем fint

------------------------------------------------------------------------------------------------------------------------

function f = fint(x)

f = exp(­-x).*sin(x);

------------------------------------------------------------------------------------------------------------------------

Затем, например, в командном окне выполним команду

>> I = quad('fint', -1, 1)

Выведем результат в формате long

I =

-0.66349146785310

Для повышения точности вычислений следует задать дополнительный четвертый аргумент:

>> I = quad('fint', -1, 1, 1.0e-10)

I =

-0.66349366663001

Второй способ.

Подынтегральную функцию можно вводить и как строку, используя команду inline:

>> F = inline('exp(-x).* sin(x)')

F =

Inline function:

F(x) = exp(-x).* sin(x)

Далее вызываем встроенную функцию quad с тремя входными аргументами, при этом имя функции пишется без апострофов:

>> I = quad(F, -1, 1)

I =

-0.66349146785310

Третий способ.

Подынтегральную функцию можно вводить, используя символ @:

>> F = @(x)exp(-x).*sin(x)

F =

@(x)exp(-x).*sin(x)

>> I = quad(F, -1, 1)

I =

-0.6635

Вычисление интегралов, зависящих от параметра.

Пусть требуется вычислить интеграл

,

где x – независимая переменная, и – параметры. Вычислим этот интеграл при значениях параметров

и .

Первый способ.

Создаем файл-функцию, зависящую от трех входных аргументов:

------------------------------------------------------------------------------------------------------------------------

function f = fparam(x, par1, par2)

f = par1.*x.^2+par2.*sin(x);

------------------------------------------------------------------------------------------------------------------------

Для вычисления интеграла используем quad, в командном окне

I = quad('fparam', -1, 1, 1.0e-06 , 0, 22.5, -5.9)

I =

15

При вычислении интеграла, зависящего от параметров, их следует указывать, начиная с шестого аргумента quad.

( Цифра ''0'' на месте пятого аргумента подавляет вывод узлов интегрирования на экран)

Второй способ.

Подынтегральную функцию вводим как строку

>> F = inline('par1.*x.^2+par2.* sin(x)','x','par1','par2')

F =

Inline function:

F(x,par1,par2) = par1.*x.^2+par2.* sin(x)

Затем снова используем quad в виде

>> I = quad(F, -1, 1,1.0e-10 , 0,22.5,-5.9)

I =

15.0000

Третий способ.

>> f = @(x, par1, par2) par1.*x.^2+par2.* sin(x)

f =

@(x,par1,par2)par1.*x.^2+par2.*sin(x)

>> I = quad(f, -1, 1,1.0e-10 , 0,22.5,-5.9)

I =

15.0000

Вычисление интегралов от функций, заданных в виде таблицы.

Пусть функция задана таблицей своих значений в точках , ( – четное) с постоянным шагом :

		………………..
		………………..

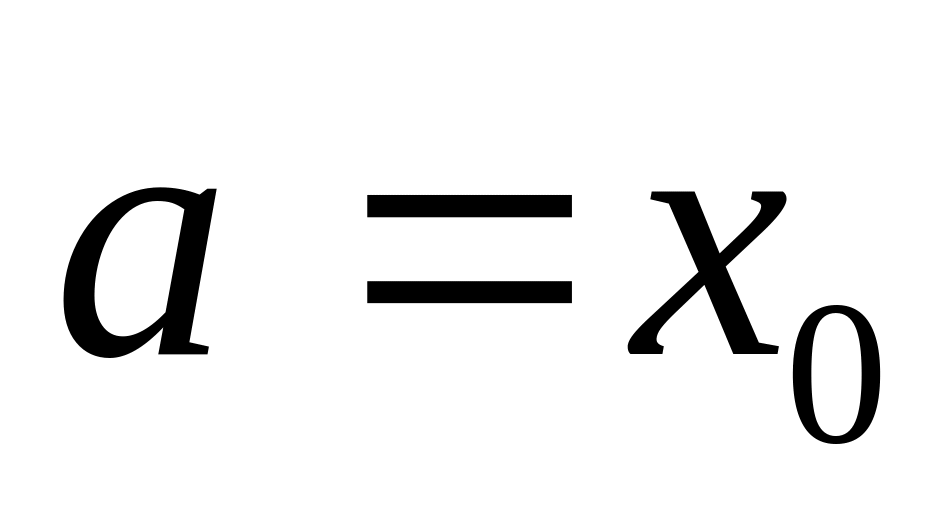
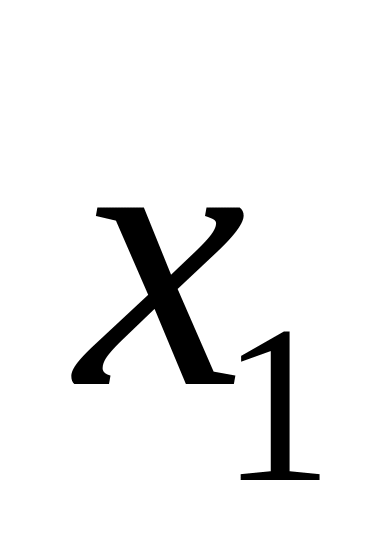
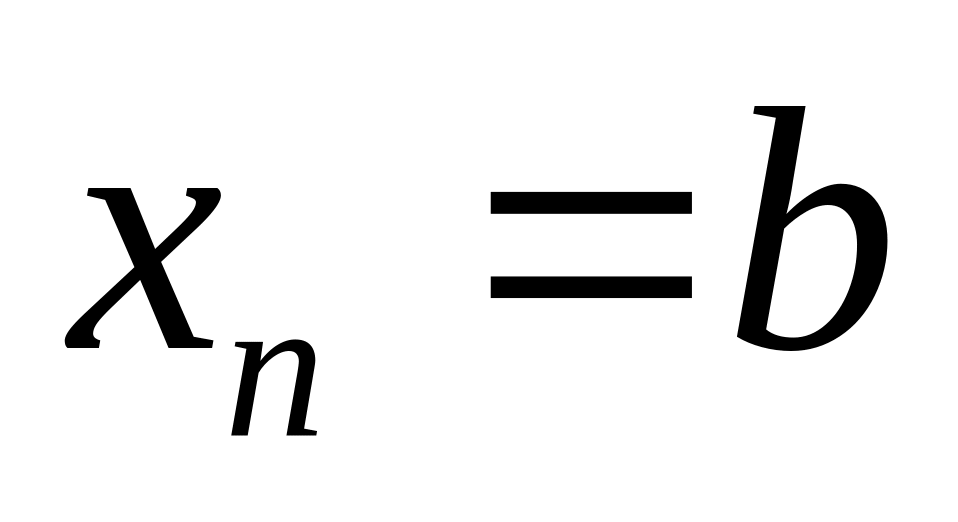
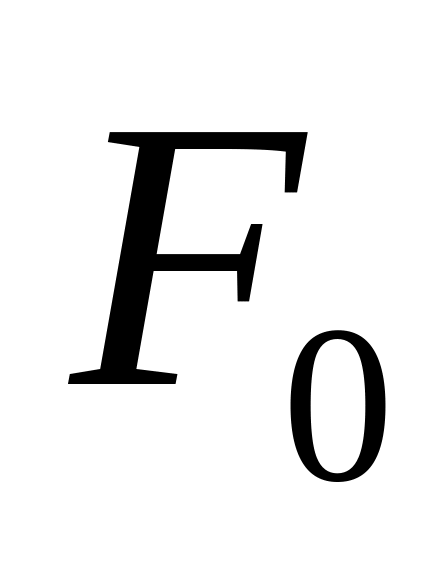
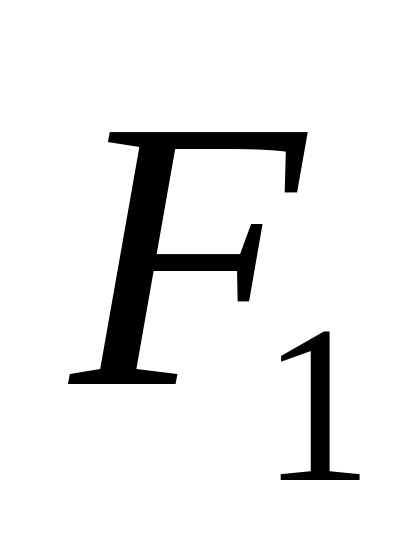
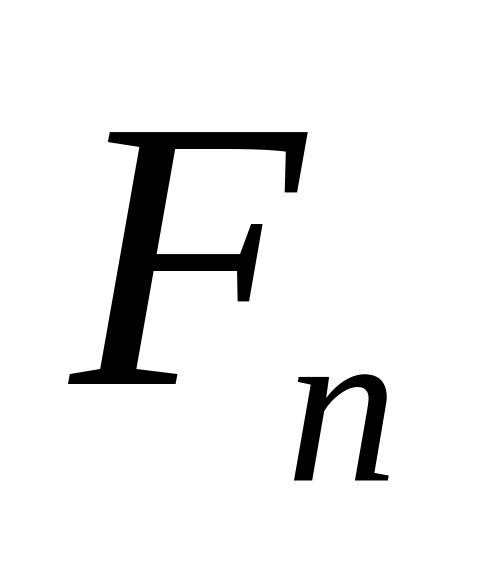
Формула Симпсона для численного интегрирования имеет вид

.

Напишем М-функцию f_simps, реализующую алгоритм метода Симпсона в MatLab

Здесь: F – вектор значений табличной функции, M – четное число интервалов на которые разделён отрезок , h – шаг таблицы.

Например, для функции создадим таблицу, разделяя отрезок на 10 интервалов и для полученной табличной функции вычислим приближенное значение интеграла , используя функцию f_simps.

Выполняем в команды:

M = 10;

a = -1;

b = 1;

h = (b-a)/M;

x = a:h:b;

F = exp(-x).*sin(x);

Int = f_simps(F, M, h)

Int =

-0.6635