Аналитическое описание

гранулометрического состава.

Для описания кривых гранулометрического состава (рис.1) в ряде случаев используются формулы. Наиболее часто применяются эмпирическая формула Розина-Раммлера и теоретическое соотношение - логарифмически нормальное распределение частиц по размерам. Один из видов записи формулы Розина-Раммлера следующий:

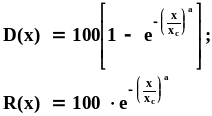(11)

где a и Х_c - постоянные; X - размер частиц.

По физическому смыслу X_c - такой размер, при котором масса частиц крупнее X_c составляет 36,8%, а мельче X_c - 63,2%. Показатель степени характеризует ширину распределения, т.е. степень однородности материала: чем больше а, тем уже материал по диапазону размеров частиц.

Для практического применения формулы Розина-Раммлера уравнение (11) дважды логарифмируется:

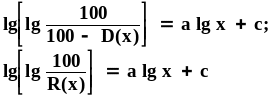(12)

где

Уравнение (12) описывает прямую в координатах , т.е. в двойной логарифмической сетке.

При этом параметр а приобретает значение тангенса угла наклона этой прямой.

Логарифмически нормальное распределение получается, если в нормальную Гауссову функцию распределения подставить в качестве аргумента логарифм диаметра частиц. Справедливость этого закона теоретически доказана академиком А.Н. Колмогоровым. Формула имеет вид

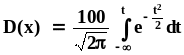(13)

где t - нормированная нормально распределенная величина, среднее значение которой равно нулю. Оно находится:

(14)

где X₅₀ - медианный размер, т.е. такой размер, по которому вся масса материала делится на две равные доли;

Lg - среднеквадратичное отклонение логарифмов диаметров от их среднего значения.

Логарифмически нормальное распределение удобно изображать графически в такой системе координат, по оси абсцисс которой откладываются логарифмы диаметров частиц, а по оси ординат - величины t, т.е. в логарифмически вероятностной логарифмической сетке. График логарифмически нормального распределения, вычерченный в такой сетке изобразится прямой линией.

Математическая модель процессов измельчения в мельницах ударно-отражательного действия

Основным методом расчета сложных процессов химической технологии является метод математического моделирования, реализующий расчет на ЭВМ и позволяющий отыскивать оптимальные режимы проведения процессов и условий управления ими.

Математическое моделирование обязательно включает три взаимосвязанные стадии:

1. формирование изучаемого процесса - построение математической модели (составление математического описания);

2. программирование решения задачи (алгоритмизация) для нахождения численных значений определяемых параметров;

3. установление соответствия (адекватности) модели изучаемому процессу.

Формализация процессов измельчения в мельницах ударно-отражательного действия

На кафедре МАХП ИГХТУ разработана математическая модель процессов помола в высокоскоростных ударно-центробежных мельницах. Процесс измельчения является сложным процессом, поэтому математическая модель составлена по участкам.

Допущения и предпосылки.

1. Диапазон имеющихся размеров частиц разбивается на n узких фракций. В этих фракциях дисперсность частиц принимается постоянной.

2. Отношение веса разрушившихся частиц к весу частиц исходной фракции называется вероятностью разрушения P(x). Считается, что вероятность разрушения количественно характеризует величину разрушившихся частиц. Разрушившимися считаются частицы перешедшие из исходной фракции в более мелкие.

3. Полученные в результате измельчения частицы материала распределяются по своим размерам в зависимости от скорости и физико-механических свойств.

Распределительная функция (x) описывает дифференциальное распределение частиц по размерам в продукте измельчения узкой исходной фракции.

Гранулометрический состав продуктов, полученных после однократного ударного нагружения частиц узкой исходной фракции размером можно представить в виде суммы неразрушившейся и разрушившейся частей. В матричной форме формула имеет вид:

(15)

где f(X_n) - доля частиц в измельченном материале;

(X_n) - приведенная доля n-ой фракции в распределительной функции (x), показывающая, какая часть материала перешла из первой фракции в

n-ую.

Каждая фракция имеет свою вероятность разрушения P(x). Поэтому при измельчении исходного многофракционного материала однократным ударом она будет вносить свой вклад в конечное распределение частиц по размерам.

Формула для расчета гранулометрического состава полученного материала в матричной форме записи имеет вид:

(16)

Введя обозначения матриц соответствующими буквами, можно записать

(17)

где - F_к(x) - матрица-столбец гранулометрического состава измельченного материала;

P(x) - диагональная матрица, которая составляется из вероятностей разрушения исходных фракций частиц;

d(x) - нижняя треугольная матрица составлена из значений распределительных функций. В первом столбце данной матрицы записывается распределение частиц по размерам, которые получаются при изменении первой фракции частиц исходного материала. Второй столбец - второй фракции и т.д.

F₀(x) - матрица-столбец гранулометрического состава исходного материала.

Расчет гранулометрического состава материала после n-кратного нагружения производится последовательно по уравнению (16).

Гранулометрический состав измельченного материала принимается за исходный для последующего нагружения.

Уравнение для расчета грансостава после n-кратного нагружения имеет вид

(17)

Для расчета гранулометрического состава измельченного материала с использованием математической модели необходимо знать зависимость вероятности их разрушения и распределительных функций от исходного размера частиц, скорости разрушения и числа нагружений. Число нагружений рассчитывается по формуле, полученной в результате математической обработки экспериментальных данных.

(18)

где Q_м - производительность мельницы, ^т/_час;

V - линейная скорость рабочих органов, ^м/_с;

X_ср - средний размер исходной монофракции, мм.

Расчетная зависимость для определения критических скоростей разрушения получена в результате математической обработки экспериментальных данных

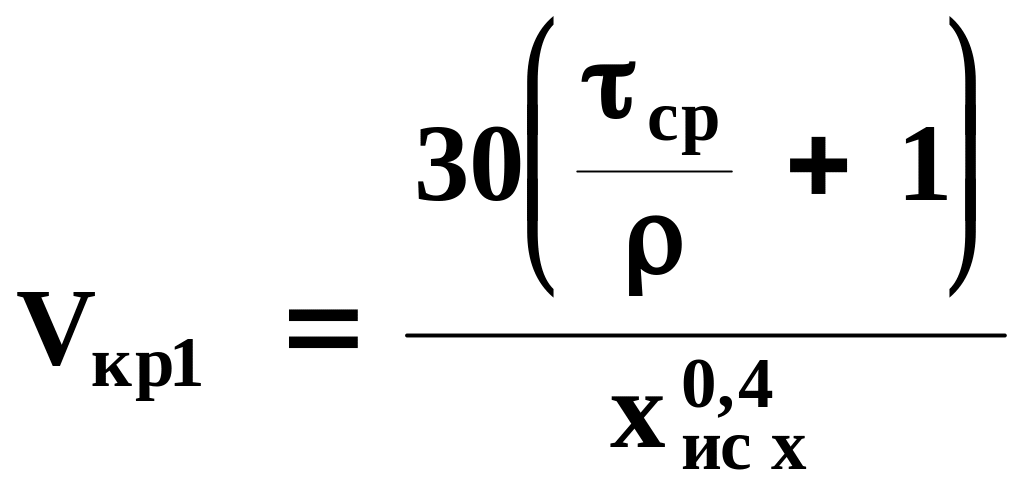, (19)

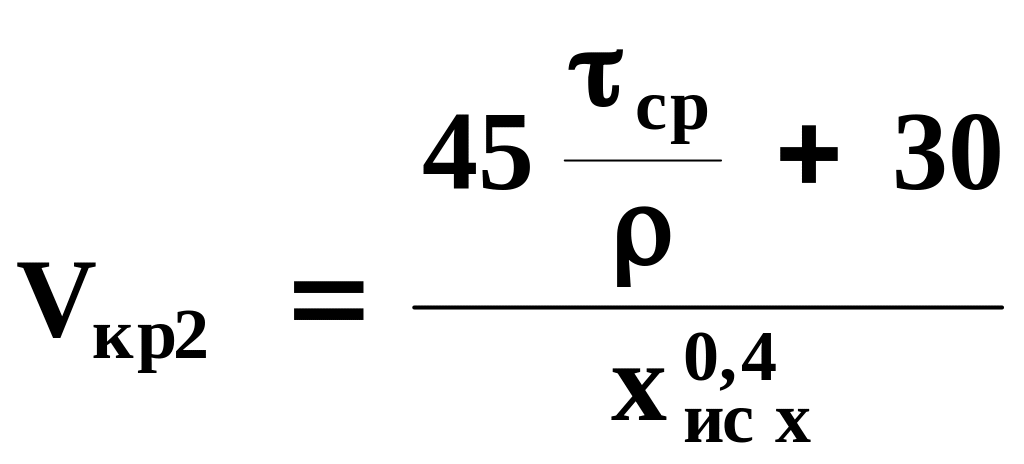, (20)

V_кр1 - критическая скорость для первого удара, ^м/_с;

V_кр2 - критическая скорость для второго и последующих ударов, ^м/_с;

 - плотность материала,^кг/_см³

_ср- предельная нагрузка на срез, ^кг/_мм²

Вероятность разрушения подсчитывается по измененному логарифмически нормальному распределению. Возможность применения к продуктам измельчения логарифмически нормального распределения частиц по размерам математически обоснована для условия достаточно большого времени измельчения, при котором можно принять, что получаемый в результате измельчения продукт не зависит от абсолютных размеров частиц исходного материала. Вероятности разрушения определим по следующим выражениям

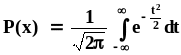(21)

Функцию безразмерного комплекса подсчитываем по уравнению

Суммарная вероятность разрушения при многократном нагружении рассчитывается по следующему уравнению

(22)

Распределительную функцию разрушившейся части материала определяем по модифицированному уравнению Розина-Раммлера

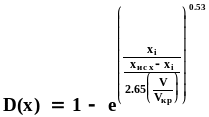, (23)

где X_исх - исходный размер частиц, мм;

X_i - текущий размер частиц, мм;

V_кр - критическая скорость разрушения, ^м/_с;

V - скорость нагружения, ^м/_с.