Лабораторная работа № 3. Вставка формул.

1. Откройте редактор Word.

2. Наберите следующий текст по образцу:

ТЕОРЕМА КОСИНУСОВ

Квадрат любой стороны треугольника равен сумме квадратов двух других его сторон без удвоенного произведения этих сторон на косинус угла между ними.

3. Давайте рассмотрим, как можно вставить формулы в текст:

1. для вставки некоторых формул достаточно просто воспользоваться кнопками Подстрочный знак и Надстрочный знак, расположенными на вкладке Главная в группе Шрифт. Наберите формулу используя подстрочный и надстрочный знак.

2. перейдите на вкладку Вставка и в группе Символы нажмите на кнопку Формула. Просмотрите формулы, содержащиеся там. Возможно, формула, которую вам необходимо вставить в текст, уже есть. В таком случае достаточно просто навести курсор на нужную вам формулу и нажатием левой кнопки мыши вставить ее в текст.

3. возможна такая ситуация, когда среди формул, есть формула, похожая на ту, которая вам необходима. Тогда при выборе похожей формулы и вставке ее в текст появляется дополнительная вкладка Работа с формулами, с помощью которой вы и сможете подредактировать вставленную формулу;

4. если же формулы, которая вам необходима, нет, то следует вызвать редактор формул (вкладка Вставка-группа Текст-кнопка Вставить объект-Microsoft Equation 3). Появится окно с шаблонами, из шаблонов выбираете соответствующие иконки и вписываете нужные символы. Если получилось так, что вы набрали формулу с ошибками, то можно кликнуть по формуле дважды и подредактировать ее. Для изменения размера формулы поставьте курсор на формулу, щелкните один раз и потяните за угол появившейся рамки.

Далее впишите следующие формулы: соs α= ;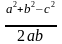

; .

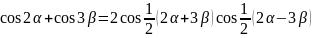4. Наберите следующий текст с формулами по образцу.

Чистая текущая стоимость

Важнейшим показателем эффективности инвестиционного проекта является чистая текущая стоимость (другие названия ЧТС – интегральный экономический эффект, чистая текущая приведенная стоимость, чистый дисконтированный доход, Net Present Value, NPV) - накопленный дисконтированный эффект за расчетный период. ЧТС рассчитывается по следующей формуле:

(1)

где П_m - приток денежных средств на m-м шаге;

O _m - отток денежных средств на m-м шаге;

- коэффициент дисконтирования на m-м шаге.

 

На практике часто пользуются модифицированной формулой:

где  - величина оттока денежных средств на m-м шаге без капиталовложений (инвестиций) К_m на том же шаге.

Для оценки эффективности инвестиционного проекта за первые К шагов расчетного периода рекомендуется использовать показатель текущей ЧТС (накопленное дисконтированное сальдо):

     

Чистая текущая стоимость используется для сопоставления инвестиционных затрат и будущих поступлений денежных средств, приведенных в эквивалентные условия.

Для определения чистой текущей стоимости прежде всего необходимо подобрать норму дисконтирования и, исходя из ее значения, найти соответствующие коэффициенты дисконтирования за анализируемый расчетный период.

После определения дисконтированной стоимости притоков и оттоков денежных средств чистая текущая стоимость определяется как разность между указанными двумя величинами. Полученный результат может быть как положительным, так и отрицательным.

Индекс доходности дисконтированных инвестиций

Индекс доходности дисконтированных инвестиций (другие названия - ИДД, рентабельность инвестиций, Profitability Index, PI) - отношение суммы дисконтированных элементов денежного потока от операционной деятельности к абсолютной величине дисконтированной суммы элементов денежного потока от инвестиционной деятельности. ИДД равен увеличенному на единицу отношению ЧТС (NPV) к накопленному дисконтированному объему инвестиций.

Ф ормула для определения ИДД имеет следующий вид:

   

или

    

При расчете ИДД могут учитываться либо все капиталовложения за расчетный период, включая вложения в замещение выбывающих основных фондов, либо только первоначальные капитальные вложения, осуществляемые до ввода предприятия в эксплуатацию. В этом случае соответствующие показатели будут иметь различные значения.