Базовые алгоритмы двухмерной графики

В компьютерной графике используется векторная и растровая графика. Данная классификация обусловлена типами устройств отображения графической информации. В настоящее время оба типа графики реализуются на растровых устройствах отображения. В них любое изображение представляет собой набор точек заданного цвета и яркости.

В векторной графике изображение представляется описанием фигур (точка, отрезок, ломаная и кривая), которые отображаются аппаратными средствами или переводятся программно в растровое представление.

К базовым алгоритмам растровой графики относят алгоритмы, решающие следующие задачи:

1. Рисование отрезка прямой;

2. Рисование дуги эллипса;

3. Заполнение замкнутой области

Алгоритм Брезенхема

Брезенхем предложил алгоритм, не требующий деления, обеспечивающий минимизацию отклонения сгенерированного образа от истинного отрезка. Основная идея алгоритма состоит в том, что если угловой коэффициент прямой меньше 1/2, то естественно точку, следующую за точкой (0,0), поставить в позицию (1,0) (рис. 1а), а если угловой коэффициент больше 1/2, то – в позицию (1,1) (рис. 1б). Для принятия решения куда заносить очередной пиксел вводится величина отклонения Е точной позиции от середины между двумя возможными растровыми точками в направлении наименьшей относительной координаты. Знак Е используется как критерий для выбора ближайшей растровой точки.

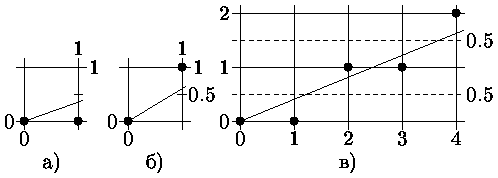
Рис. 1

Если Е < 0, то точное Y-значение округляется до последнего меньшего целочисленного значения Y, т.е. Y-координата не меняется по сравнению с предыдущей точкой. В противном случае Y увеличивается на 1.

Для вычисления Е без ограничения общности упрощающе положим, что рассматриваемый вектор начинается в точке (0,0) и проходит через точку (4, 1.5) (см. рис. 1в), т.е. имеет положительный наклон меньший 1.

Из рис. в видно, отклонение для первого шага:

Е1 = Py/Px - 1/2 < 0,

поэтому для занесения пиксела выбирается точка (1,0).

Отклонение для второго шага вычисляется добавлением приращения Y-координаты для следующей X-позиции (см. рис. в):

Е2 = Е1 + Py/Px > 0,

поэтому для занесения пиксела выбирается точка (2,1). Так как отклонение считается от Y-координаты, которая теперь увеличилась на 1, то из накопленного отклонения для вычисления последующих отклонений надо вычесть 1:

Е2 = Е2 – 1

Отклонение для третьего шага:

Е3 = Е2 + Py/Px < 0,

поэтому для занесения пиксела выбирается точка (3,1).

Суммируя и обозначая большими буквами растровые точки, а маленькими - точки вектора, получаем:

Е1 = y1 - 1/2 = dY/dX - ½

Возможны случаи:

1. Е1 > 0

ближайшая точка есть: X1 = X0 + 1;    Y1 = Y0 + 1;

E2 = Е1 + Py/Px - 1;

2. Е1 < 0

ближайшая точка есть: X1 = X0 + 1;     Y1 = Y0;

E2 = E1 + Py/Px.

Так как интересует только знак Е, то можно избавиться от неудобные частных умножением E на 2×Px:

E1 = 2×Py – Px

E1 > 0 E2 = E1 + 2×(Py - Px)

Е1 < 0

E2 = E1 + 2×Py

Таким образом получается алгоритм, в котором используются только целые числа, сложение, вычитание и сдвиг: X= x1; Y= y1; Px= x2 - x1; Py= y2 - y1; E= 2*Py - Px; i= Px; PutPixel(X, Y); /* Первая точка вектора */ while (i= i- 1 і 0) { if (E і 0) { X= X + 1; Y= Y + 1; E= E + 2*(Py - Px); } else X= X + 1; E= E + 2*Py; PutPixel(X, Y); /* Очередная точка вектора */ }

Этот алгоритм пригоден для случая 0 < dY < dX. Для других случаев алгоритм строится аналогичным образом.

На рис.  приведен пример генерации по алгоритму Брезенхема того же самого отрезка, что и показанного на рис. 2 для генерации по алгоритму несимметричного ЦДА. Из сравнения рисунков видно, что результаты различны.

Рис. 2Генерация отрезка по алгоритму Брезенхема

В Приложении 2 приведена программа V_BRE, реализующая описанный выше алгоритм.

Разработаны алгоритмы цифрового генератора для окружностей и других конических сечений.

Модифицированный алгоритм Брезенхема

Основная идея алгоритма состоит в том, чтобы для ребер многоугольника устанавливать яркость пиксела пропорционально площади пиксела, попавшей внутрь многоугольника.

На рис.  приведена иллюстрация построения ребра многоугольника с тангенсом угла наклона 11/21.

На рис.3 а) показан результат генерации многоугольника с использованием ранее рассмотренного алгоритма Брезенхема при двухуровневом изображении (пиксел или закрашен или не закрашен).

На рис.3 б) показан результат генерации многоугольника с вычислением интесивности пикселов, через которые проходит ребро многоугольника. Интенсивность вычисляется пропорциональной площади части пиксела, попавшей внутрь многоугольника.

На рис. 3в) показан результат генерации многоугольника с вычислением интесивности пиксела, через который проходит ребро многоугольника в соответствии с модифицированным алгоритмом Брезенхема.

Как видно из рис.  при построении ребра многоугольника с тангенсом угла наклона t  (0  t  1) могут захватываться либо один пиксел (пикселы (0,0), (2,1), (4,2), (6,8)) либо два пиксела (пикселы (1,0) и (1,1), (3,1) и (3,2), (5,2) и (5,3)). Если захватывается один пиксел, то часть его площади, попавшая внутрь многоугольника, равна dy + t/2 (рис.3 a).

Если же захватывается два пиксела, то часть площади нижнего пиксела, попавшая внутрь многоугольника равна 1 - [((1 - dy)²)/ 2t], а верхнего - [((dy - 1 + 2)²)/ 2t] (см. рис. б). Суммарная площадь частей для двух пикселов, попавшая внутрь многоугольника, равна dy + t/2.

Если теперь в исходном алгоритме Брезенхема заменить отклонение E на E' = E + (1-t), то 0  E'  1) и значение E' будет давать значение той части площади пиксела, которая находится внутри многоугольника.

Выполняя преобразование над значением отклонения для первого шага получим, что начальное значение станет равным 1/2. Максимальное значение отклонения E'_max, при превышении которого производится увеличение Y-координаты занесения пикселов, станет равным (1 - t).

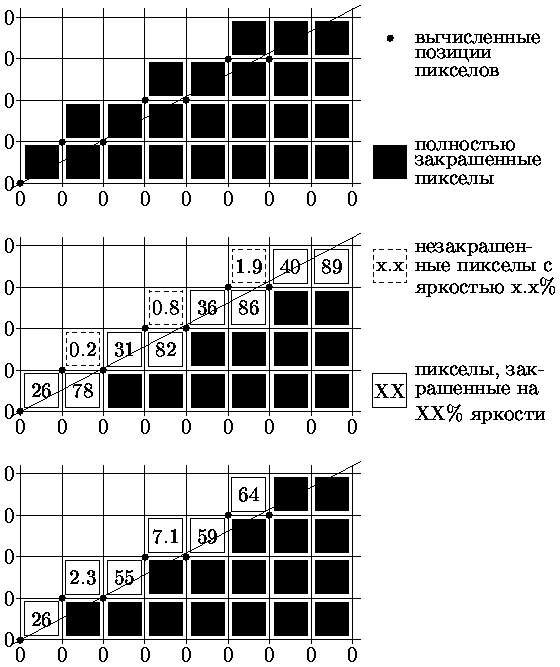
Рис. 3: Устранение ступенчатости ребер многоугольника: а) генерация ребер без устранения ступенчатости; б) точное вычисление интенсивности пикселов границы; в) формирование пикселов границы по модифицированному методу Брезенхема.

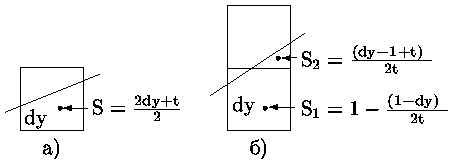
Рис.4: Устранение ступенчатости за счет учета площади пикселов, пересекаемых ребром многоугольника.

Для того, чтобы оперировать не дробной частью максимальной интенсивности, а непосредственно ее значениями достаточно домножить на полное число уровней интенсивности I тангенс угла наклона (t), начальное (E') и максимальное (E'_max) значения отклонения.

В результате получается следующий алгоритм, пригодный для случая 0       dY       dX: X= x1; Y= y1; Px= x2 - x1; Py= y2 - y1; t= IPy / Px; E'= I/2; E'_max= I - IPy / Px; i= Px; PutPixel(X, Y, t/2); /* Первая точка вектора */ while (i = i - 1  0) { if (E'  E'_max) { X= X + 1; Y= Y + 1; E' = E'- E'_max; } else X= X + 1; E' = E'+ t; PutPixel(X, Y, E'); /* Очередная точка вектора */ }

Для избавления от вещественной арифметики при манипулировании с E' можно домножить уже упомянутые величины на 2Px. Но в этом случае при занесении пикселов потребуется деление E' на 2Px.