3. Представление деревьев в памяти компьютера: последовательное и связанное размещение элементов.

Теперь мы обратимся к проблеме представления деревьев. Ясно, что изображение таких рекурсивных структур (точнее, рекурсивно определенных) с разветвлениями предполагает использование ссылок. Очевидно, что не имеет смысла описывать переменные с фиксированной древовидной структурой, вместо этого узлы определяются как переменные с фиксированной структурой, т. е. фиксированного типа, где степень дерева определяет число компонент-ссылок, указы­вающих на поддеревья данного узла.

Рис. 3.1. Выражение (a + b/c)*(d— e'*J), представленное в виде дерева.

Ясно, что ссылка на пустое поддерево обозначается через nil. Следовательно, дерево на рис. 3.3. состоит из компонент такого типа.

и может строиться, как показано на рис. 3.2.

Ясно, что существуют способы представления абстрактной древовидной структуры в терминах других типов данных, например таких, как массив. Это — общепринятый способ во всех языках, где нет средств динамического размещения ком­понент и указания их с помощью ссылок.

и со значениями компонент, приведенными в табл. 3.1. Хотя подразумевается, что массив t представляет абстракт­ную структуру дерева, мы будем называть его все же не дере­вом, а массивом согласно явному определению. Мы не будем обсуждать другие возможные представления деревьев в си­стемах, где отсутствует динамическое распределение памяти, поскольку мы считаем, что системы программирования и язы­ки, имеющие это свойство, являются или станут широко распространенными.

Рис. 3.2. Дерево, представленное как структура данных.

Таблица 3.1. Дерево, представленное с помощью массива

*	2	3
+	6	4
-	9	5
/	7	8
*	10	11
а	0	0
Ь	0	0
с	0	0
d	0	0
е	0	0
f	0	0

Прежде чем обсуждать, как лучше использовать деревья и как выполнять операции с деревьями, мы покажем на примере, как программа может строить дерево. Предположим, что нужно сформировать дерево, содержащее узлы типа, а значениями узлов будут п чисел, прочи­танных из входного файла. Для усложнения задачи потре­буем построить дерево с п узлами и минимальной высотой.

Чтобы достичь минимальной высоты при данном числе узлов, нужно располагать максимально возможное число уз­лов на всех уровнях, кроме самого нижнего. Это можно сде­лать очень просто, если распределять все поступающие узлы

Рис. 3.3. Идеально сбалансированные деревья.

поровну слева и справа от каждого узла. В результате по­строенное дерево при данном п имеет вид, как показано на рис. 3.3 для п = 1, ..., 7.

N = 3.

Правило равномерного распределения при известном числе узлов п лучше всего формулируется с помощью рекурсии:

1.Взять один узел в качестве корня.

2.Построить левое поддерево с nl = n div2 узлами тем же способом.

3.Построить правое поддерево с пг — п — nl— 1 узлами тем же способом. Дерево идеально сбалансировано, если для каждого его узла количества узлов в левом и правом поддереве раз­личаются не более чем на 1.

4.Предположим, например, что имеются следующие входные данные для дерева с 21 узлом:

21 8 9 11 15 19 20 21 7 3 2 15 6 4 13 14 10 12 17 16 18

Тогда алгоритм строит идеально сбалансированное де­рево, показанное на рис. 3.4.

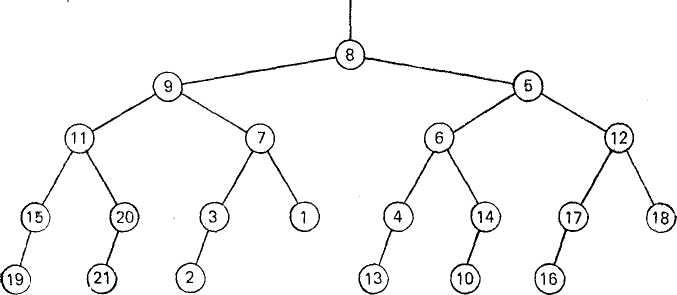
Рис. 3.4. Дерево.

Отметим простоту и ясность этой программы, достигнутые благодаря использованию рекурсивных процедур. Очевидно, что рекурсивные алгоритмы особенно уместны, когда про­грамма должна обрабатывать данные, структура которых определена рекурсивно.

Преимущество рекурсивного алгоритма особенно наглядно по сравнению с его нерекурсивной формулировкой. Читателю предлагается проявить свою изобретательность и написать нерекурсивную программу, строящую такие же деревья, прежде чем смотреть на .Эта программа приведена без дальнейших комментариев и может служить упражнением для читателя. Ему предлагается выяснить, как и почему она работает.

Деревья можно представлять с помощью связных списков и массивов (или последовательных списков).

Чаще всего используется связное представление деревьев, т.к. оно очень сильно напоминает логическое. Связное хранение состоит в том, что задается связь от отца к сыновьям. В бинарном дереве имеется два указателя, поэтому удобно узел представить в виде структуры:

LPTR

DATA

RPTR

где LPTR - указатель на левое поддерево, RPTR - указатель на правое поддерево, DATA - содержит информацию, связанную с вершиной.

Рассмотрим машинное представление бинарного дерева, изображенного на рис. 3.5.

Рис. 3.5 Логическое представление дерева

Рис. 3.6. Машинное связное представление дерева представленного на рис.3.5

Рассмотрим последовательное представление деревьев. Оно удобно и эффективно в случае, если древовидная структура в течение времени своего существования не подвергается значительным изменениям, за счет включения вершин, удаления вершин и т.д.

Выбор метода последовательного представления деревьев определяется также набором тех операций, которые должны быть выполнены над древовидными структурами. (Пример статистической древовидной структуры - пирамидальный метод сортировки). Простейший метод представления дерева в виде последовательной структуры заключается во введении вектора, задающего отбор для всех его вершин. Этот метод можно использовать также для представления леса. Недостаток метода - он не отображает упорядочения вершин дерева. Если в предыдущем примере поменять местами вершины 9 и 10, последовательное представление останется тем же.

Рис. 3.7. Диаграммы дерева: а) исходное б) перестройка в бинарное