Лабораторная Работа № 6 истечение через отверстия и насадки

Цель работы:

Определение параметров, характеризующих процессы истечения жидкости через отверстия и насадки, сопоставление расчетных и опытных параметров, характеризующих указанные процессы.

В работе необходимо:

- визуально наблюдать форму струи воды при истечении ее из отверстий и насадок различных форм и габаритов;

- по результатам опытов и расчетов определить коэффициент скорости, коэффициент сжатия струи и коэффициент расхода для истечения из отверстия и насадка при постоянном напоре;

- измерить разрежение в насадке и сравнить его с расчетным значением;

- сделать выводы по результатам сравнения опытных и расчетных значений величин.

Основные теоретические положения

Процессом истечения называется процесс прохождения жидкости через отверстия, при котором потенциальная энергия положения жидкости с большими или меньшими потерями преобразуется в кинетическую энергию вытекающей струи. Различают истечение жидкости через отверстие в тонкой стенке или просто отверстие (рис. 6.1, а) и через насадок (рис. 6.1, б).

Тонкой стенкой, по сравнению с отверстием, называют стенку, толщина _ст которой меньше диаметра d_о отверстия, т.е. _ст / d_о < 1. Насадком называют канал (трубку), длина l которого не менее 2…3 диаметров отверстия, т.е. l  (2...3)d_о. Согласно определению роль насадка может выполнять и отверстие в тонкой стенке, толщина _ст которой удовлетворяет равенству _ст  (2...3)d_о. При истечении жидкости через отверстие струя из-за действия сил инерции на расстоянии одного – двух диаметров от отверстия сжимается и не заполняет всю выходную площадь (т.е. F_c < F_о или d_с < d_о). Для насадка же струя успевает развернуться и заполняет все его выходное сечение F_н = F_о. При этом на выходе для истечения в атмосферу устанавливается атмосферное давление р_н, а в узком сечении струи будет разрежение с абсолютным давлением р_с. Величина вакуума ∆h_вак в узком сечении определяется равенством:

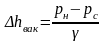. (6.1)

Наибольшее возможное значение разрежения ∆h_{вак.мах} по расчету зависит от напора, например, высоты H уровня жидкости над отверстием и составляет:

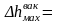0,75Н. (6.2)

Рис. 6.1

Чем больше напор, тем глубже разрежение. При определенных достаточно больших значениях Н струя уже не успевает развернуться в насадке и установится второй режим истечения через насадок – с отрывом струи от стенки. При этом насадок будет работать как отверстие в тонкой стенке, без разрежения. (Этот же режим наступит, если вакуумированное сечение насадка искусственно сообщить с атмосферой). Примечание: Все вышесказанное характерно для основного случая истечения – истечения капельной жидкости в газ, т.е. истечение через незатопленное отверстие. Случай «жидкость в жидкость» (затопленное отверстие) имеет свои особенности и здесь не рассматривается. Кроме того, различают истечение через прямые струйные каналы (незакрученная струя) и через каналы с подкруткой жидкости за счет специальных механических устройств (закрученная струя). Последний случай – так называемое истечение через центробежные форсунки – здесь также не рассматривается.

Процесс истечения реальной (вязкой и инерционной) жидкости характеризуется несколькими коэффициентами, определяющими отличие этого процесса от истечения идеальной жидкости.

В случае идеальной жидкости полагают, что потерь напора нет и струя заполняет все выходное сечение отверстия или насадка. Записав для этого случая уравнение Бернулли (2.2), легко получить формулу Э. Торричелли для расчета теоретических (идеальных) значений скорости _т

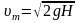, (6.3)

а также соотношение для расчета теоретического расхода Q_т через отверстие (насадок) площадью F_о

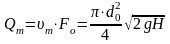. (6.3a)

В действительности, из-за потерь напора (в первую очередь на местные сопротивления, т.к. путевые потери из-за небольшой протяженности канала отверстий – малы) скорость истечения _д меньше _т. Это учитывается коэффициентом скорости φ, который связан с коэффициентом местного гидравлического сопротивления ξ равенством:

(6.4)

Значение величины действительной скорости _д равно:

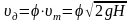. (6.4a)

Коэффициент φ зависит от числа Re и с ростом Re в связи с уменьшением  увеличивается (рис. 6.2). Для отверстия при истечении маловязких жидкостей (вода, бензин и т.д.) с достаточно большими числами Rе, можно приближенно принимать φ_отв = 0,96...0,97.

Для насадка на основном – первом режиме φ_н = 0,8...0,82 (на втором – срывном, как и для отверстия, φ_н = φ_отв = 0,96…0,97), т.е. скорость истечения через насадок при прочих равных условиях на основном режиме меньше, чем через отверстие в тонкой стенке.

Степень сжатия струи оценивается коэффициентом сжатия струи ε:

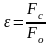; (6.5)

отсюда

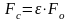. (6.5a)

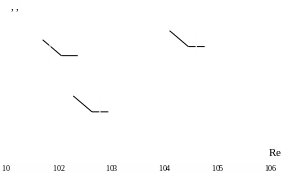
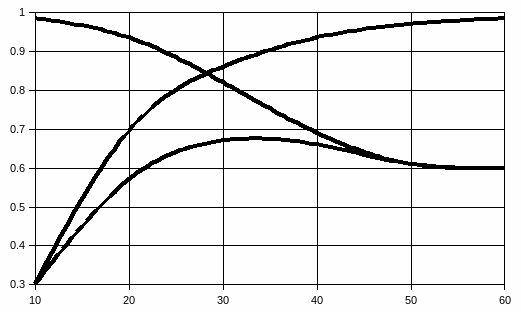
Рис. 6.2

Причем для отверстия можно принимать ε_отв = 0,63...0,64, а для насадка на безотрывном (первом) режиме ε_н = 1. (Для отверстия, с ростом числа Re сжатие струи увеличивается, т.к. поток обладает большей инерционностью, см. рис. 6.2).

Действительный расход Q_д жидкости при истечении реальной жидкости из отверстия или насадка определяется произведением площади струи F_с на действительную скорость _д и будет меньше теоретического:

.

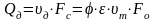или (6.6)

.

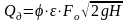Это отличие учитывается коэффициентом расхода μ:

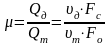. (6.7)

Таким образом, коэффициент расхода  всегда меньше единицы и учитывает наличие гидравлических потерь напора и сжатие струи при истечении реальной жидкости из отверстия или насадка. Из сопоставления зависимостей (6.6), (6.3 а) и (6.7) следует расчетная формула для μ:

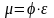. (6.8)

Зависимость μ, φ, ε от числа Rе для истечения из малого отверстия в тонкой стенки показана на рис. 6.2. При расчетах для этого случая можно принимать μ = 0,6...0,61. Для насадка же μ_н = φ_н = 0,8…0,82 (на первом режиме). Следовательно, для истечения из насадка расход при прочих разных условиях на первом (безотрывном) режиме будет больше, чем для отверстия, несмотря на меньшую скорость выхода.

Поскольку скорость выхода струи определяет ее «вылет» (расстояние по горизонтали X), а силы гравитации определяют ее «снижение» (расстояние по вертикали У), то по измеренным параметрам Х и У (параметры баллистической траектории) можно опытным путем определить значение φ_опыт:

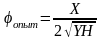. (6.9)

В се вышесказанное относится к истечению жидкости через отверстия любых форм. Но для отверстий полигональных форм по мере полета струи происходит изменение сечения – инверсия струи (строго говоря, это проявляется и на круглом отверстии, но менее отчетливо). Инверсия происходит под действием сил гравитации (сплющивание круглой струи), инерции (разная скорость по сечению струи) и главное – сил поверхностного натяжения. Благодаря последним – углы в сечении струи сначала притупляются, а затем, по мере движения, выступы переходят во впадины, образуя красивые «звезды» (рис. 6.3).

Рис. 6.3

Образование «звезд» в сечениях струи происходит быстро, и обычно удается отчетливо наблюдать лишь переход от начальной формы к конечной (четвертой – на рис. 6.3).

Описание экспериментальной установки

Схема установки показана на рис. 6.4 для варианта истечения из насадка. Истечение из бака 1 под напором Н, который определяется по пьезометру 2, происходит через насадок 4, разрежение в котором по отношению к окружающему (атмосферному давлении) измеряют вакуумметром 3.

Параметры Х, У баллистической траектории струи определяют (только для истечения из отверстия) с помощью катетометра (вертикальной и горизонтальной линеек); вес жидкости G, которая будет попадать в мерный сосуд 5, определяют с помощью весов 6, а время наполнения t – по секундомеру 7.

Установка позволяет достаточно просто присоединять к выходу из бака 1 отверстия и насадка разной длины и формы: путем вращения диска, на котором выполнены разные отверстия и установлены разные насадки.

Порядок выполнения работы

1. Перед началом опыта необходимо проверить наличие воды в баке 1 по водомерному стеклу 2 – величина Н должна быть не менее 200 см.

Рис. 6.4

2. Установить диск с отверстиями так, чтобы истечение происходило из круглого отверстия в тонкой стенке. Одновременно отрегулировать положение мерной емкости «на измерение». Измерить вес жидкости G, поступившей в емкость 6 за время t (по секундомеру 7), с помощью весов 5. Измерить также величины X и У.

3. Переставить с помощью штурвала диск на истечение из «цилиндрического» насадка и произвести те же измерения (без параметров баллистической траектории) при наличии вакуума в узком месте струи. Для установления вакуума предварительно следует исключить сообщение внутренней части насадка 4 с атмосферой, которое происходит через трубку от вакуумметра 3. С этой целью кратковременно перекрывается отверстие выхода из насадка 4 – жидкость потечет через трубку к вакуумметру 3, после чего эта резиновая трубка перегибается, а выходное сечение насадка – открывается. Наряду с измерениями G, t и Н осуществляется измерение и ∆h_вак по вакуумметру 3 (его следует выразить в см водяного столба).

4. Переставить последовательно диск так, чтобы можно было визуально наблюдать истечение из отверстий квадратной и треугольной форм. Сделать зарисовки инверсии струи для таких отверстий.

5. Оформить протокол работы, изобразив в нем схему установки с вариантами истечения из отверстия и насадка, эскизами инверсии струи и расчетами. В качестве расчетных зависимостей использовать формулы: (2.4) – для подсчета опытного расхода; (6.3 а), (6.7) – для подсчета теоретического расхода и коэффициента расхода; (6.9) – для коэффициента скорости при истечении из отверстия (для насадки φ_н = μ_н); (6.8) – для коэффициента сжатия в отверстии (в насадке ε = 1); (6.4) – для коэффициента сопротивления. Справочные значения этих величин приведены на с. 36-38.

6. Сопоставить расчетные и опытные значения основных коэффициентов и сделать вывод по работе.

Контрольные вопросы

1. Общая характеристика процесса истечения жидкости из отверстий и насадок. Смысл основных коэффициентов.

2. Особенность истечения через отверстие в тонкой стенке. Зависимость коэффициентов , , и  от числа Rе (пояснить).

3. Особенности истечения через насадок. Характерные значения величин коэффициентов , , и , причины образования вакуума.

4. Расчетные зависимости для расхода и скорости истечения жидкости.

5. Записать уравнение Бернулли для случаев истечения, взяв два сечения – на поверхности жидкости в баке и на выходе из отверстия. Пояснить величины.

6. Принцип определения действительного расхода жидкости и коэффициента скорости в опыте.

Рекомендуемая литература

[1, с. 122-126, 129-132]. [3, с. 90-93, 95-96]. [4, с. 379-384, 388-395].