Лабораторная Работа № 4 определение потерь напора по длине трубы

Цель работы:

Сопоставление результатов экспериментального и расчетного определения коэффициента путевых потерь напора при течении жидкости в прямой цилиндрической трубе.

В работе необходимо:

- опытным путем определить потери напора на заданном участке прямой трубы при установившемся движении воды;

- обработать результаты опыта, определив число Рейнольдса и коэффициент путевых потерь напора в опыте;

- рассчитать для полученного из опыта числа Рейнольдса коэффициент путевых потерь  по известным зависимостям и сопоставить его величину с опытным значением.

Основные теоретические положения

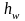Гидравлические потери удельной энергии потока жидкости (напора) по длине l трубы или путевые гидравлические потери зависят от длины и диаметра d трубы, скорости течения , вязкости жидкости, параметров канала (формы, шероховатости). Во многих случаях гидравлические потери пропорциональны квадрату средней скорости течения (удельной кинетической энергии единицы веса жидкости). Эта зависимость называется формулой Вейсбаха:

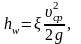м, (4.1)

где  – коэффициент гидравлического сопротивления (гидросопротивления);

h_w – удельные потери напора, м;

_cp – средняя скорость, м/с.

Удельную кинетическую энергию называют скоростным напором. Коэффициент гидросопротивления, таким образом, есть отношение потерянного напора к напору скоростному.

Поскольку потери напора зависят от скорости, а приводят, как правило, к потери напора (давления), то величина коэффициента  может быть самой различной: от близких нулю (для идеальной жидкости, лишенной потерь) до очень больших значений.

Существуют путевые и местные потери напора жидкости. В этой работе будут рассматриваться только путевые потери. Путевые потери возникают на определенной длине канала l вследствие вязкостного трения, соударения частиц и завихрения потока (поскольку все эти причины связаны с внутренним трением в жидкости, часто они обобщенно обозначаются как «потери на трение»). Для этих потерь коэффициент  в формуле (4.1) выражают через коэффициент путевых потерь λ и безразмерную длину l/d:

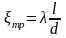, (4.2)

с учетом этого формула (4.1) запишется так:

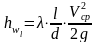. (4.2а)

Эта формула, как и коэффициент λ, называется по имени ученого Дарси.

Для ламинарного режима течения (Re < Re_кр) коэффициент Дарси  определяется только интенсивностью сил вязкостного трения. Здесь он обратно пропорционален числу Рейнольдса:

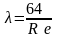. (4.3)

С учетом выражения для числа Re (см. формулу 3.1), из зависимости (4.2а) следует, что потери прямо пропорциональны скорости   (или расходу) жидкости, т.е., как отмечалось в работе № 3, закон сопротивления = f() для ламинарного режима течения – линейный (рис. 4.1, а).

Рис. 4.1

Для турбулентного режима (Re > Re_кр) при сравнительно малых числах Рейнольдса (до 10⁵) путевые потери напора определяются соударением частиц в ядре потока при их турбулентных пульсациях. Для этих чисел Re справедлива опытная формула Блазиуса:

. (4.4)

Шероховатость стенок трубы в этом случае не влияет на сопротивление (выступы скрыты в ламинарном пограничном слое, медленно движущемся у стенок). Поэтому течение при таких числах Рейнольдса (Re_кр > Re ≤ 10⁵) называют течением в гидравлически гладких трубах.

При числах Re > 10⁶, вследствие уменьшения ламинарного подслоя пограничного слоя жидкости бугорки шероховатости К_э оказывают определяющее влияние на потери – это течение в шероховатых трубах (зона квадратичного сопротивления), т.е. здесь  ² (рис. 4.1в).

Здесь уже λ практически не зависит от Re:

. (4.4а)

В настоящее время часто применяют формулу, предложенную А.Д. Альтшулем и обобщающую формулы (4.4) и (4.4 а), ее можно применять во всем диапазоне чисел Re для турбулентного режима:

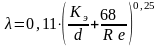. (4.4б)

Значения эквивалентной абсолютной шероховатости К_э (средней высоты бугорков шероховатости) или ее относительной величины, К_э/d приводятся в справочниках и зависят от материала труб, способа их изготовления, срока и условий службы. Например, для старых водопроводных труб высота К_э бугорков шероховатости равна 0,5 мм.

Из анализа зависимостей (4.1), (4.2) и (4.4 б) следует, что для турбулентного режима течения путевые потери напора зависят от скорости жидкости (или расхода) в степени 1,75…2 (  ^1,75…2 ), т.е. закон сопротивления для этого режима близок к квадратичному.

Описание экспериментальной установки

Основным элементом установки является прямая цилиндрическая труба 2 диаметром d (рис. 4.2), в которой установлены пьезометры 3 на расстоянии l между ними. При открытом вентиле 4 по трубе 2 протекает вода из бака 1 на слив или в мерную емкость 5.

Рис. 4.2

Поскольку уровень воды в баке 1 практически не меняется, течение в трубе –установившееся. Количество жидкости, поступившее в емкость 5 за определенный промежуток времени t (измеренный секундомером), взвешивается на весах 6. Опытные потери напора по длине трубы определяются разностью показаний пьезометров в сечениях 1 и 2.

Порядок выполнения работы

1. На бланке вычертить схему установки, выписать исходные данные и расчетные формулы: (2.3); (2.4); (3.1); (4.2 а); (4.3); (4.4). Кроме этих формул, будет также использовано уравнение Бернулли (2.1), которое для условий опыта (горизонтальная цилиндрическая прямая труба, установившееся течение) запишется так:

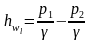. (4.5)

2. Перед началом работы необходимо убедиться в наличии воды в баке по пьезометрам (уровень должен быть не ниже 100 см по шкале на стенде пьезометров).

3. Открыть вентиль 4 и в трубе 2 установить течение воды на слив. Через некоторое время под выходной срез трубы 2 подставить емкость 5 и синхронно включить секундомер, выключаемый затем одновременно с отставлением емкости 5. Время наполнения не должно быть меньше 10 с для уменьшения ошибки в определении расхода. (Измерение производят с этой же целью дважды и результаты осредняют). Одновременно (дважды) снимаются показания пьезометров .

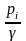4. Данные опыта обработать в такой последовательности: определить вес жидкости G, затем объемный расход Q по (2.4), подсчитать скорость (по 2.3) и после определения потерь (по 4.5) из формулы (4.2 а) найти опытное значение коэффициента λ_оп. Затем определить число Re по (3.1) и расчетное значение λ_расч. В соответствии с числом Re выбирается одна из формул – (4.3), (4.4) или (4.4 а, б). Чаще всего реализуется турбулентный режим течения в гидравлически гладких трубах и используется формула (4.4).

5. Величины опытного λ_оп и расчетного λ_расч коэффициентов Дарси сопоставить между собой и сделать вывод об их сходимости, возможных причинах несовпадения.

Контрольные вопросы

1. Общая характеристика потерь напора, расчетные формулы и входящие в них величины.

2. Влияние различных факторов на коэффициент путевых потерь.

3. Законы сопротивления для ламинарного и турбулентного режимов течения.

4. Порядок определения коэффициента λ в опыте. Как при этом используется уравнение Бернулли?

Рекомендуемая литература

[1, с. 52-55, 79, 95-96, 98, 100], [3, с. 54, 63, 72-73, 80-83], [5, с. 50-92].