Лабораторная Работа № 3 изучение режимов движения жидкости
Цель работы:
Ознакомление с особенностями течения жидкости при ламинарном и турбулентном режимах движения в круглой цилиндрической трубе.
В работе необходимо:
- визуально наблюдать изменения характера движения частичек подкрашенной воды при различных скоростях в круглой цилиндрической трубе;
- определить числа Рейнольдса, характеризующие режимы движение воды при исследуемых скоростях потока, и сделать заключения о режимах течения воды в опытах.
Основные теоретические положения
Д.И. Менделеев (1880 г.) предположил, а английский физик Осборн Рейнольдс экспериментально показал, что в природе существуют два режима течения вязкой жидкости: ламинарный и турбулентный.
Ламинарный режим. Течение жидкости при ламинарном режиме – слоистое, струйное без перемешивания частиц между слоями и без пульсаций скорости. Форма линий тока для такого режима течения определяется формой русла, и для прямой трубы все линии тока параллельны оси трубы. Подкрашенная струйка в потоке такой жидкости практически не размывается и движется по прямой горизонтальной линии параллельно оси канала (рис. 3.2, а). Если частички краски растворимы в воде, то возможна диффузия раствора из ядра потока к стенкам трубы по мере движения струи. Для такого режима определяющими (главными) силами являются силы вязкостного трения.
Ламинарный режим
характеризуется: параболическим законом
изменения скорости по сечению трубы
(от нуля на стенке – до максимальной
скорости в центре ядра (рис. 3.1, а));
линейным законом сопротивления
(зависимостью путевых потерь напора
от расхода или скорости ,
т.е.
);
гиперболической зависимостью коэффициента
путевых потерь напора
от скорости течения
.
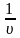Этот режим течения имеет место при
малых скоростях движения или для
высоковязких жидкостей. Для него
коэффициент Кориолиса в уравнении
Бернулли (формула 2.1) может быть принят
равным 2. О. Рейнольдс установил
безразмерный критерий Re,
названный его именем и определяющий
вероятный режим течения:
,
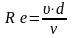(3.1)
где – средняя скорость движения в рассматриваемом сечении, м/с;
d – характерный размер (для трубы – диаметр), м;
ν – кинематический коэффициент вязкости, м2/с. Для воды при комнатной температуре можно принимать ν = 10-6 м2/с (1 сантистокс).
Критерий Рейнольдса характеризует соотношение между силами инерции и силами вязкого трения в потоке реальной жидкости. Критическое число Reкр устанавливает наиболее вероятную границу перехода ламинарного режима течения в турбулентный. Обычно оно принимается равным Reкр = 2300, но следует иметь в виду, что переход может произойти и раньше (при условии искусственной турбулизации потока), и позднее. Поэтому многие исследователи выделяют не одно какое-то значение числа Reкр, а границы переходного режима (Reкр = 1800...3000).
С помощью этого критерия можно установить, какой реализуется режим течения жидкости – ламинарный или турбулентный. Если рассчитанное для данного опыта значение Re будет меньше критического значения, то течение вероятнее всего будет ламинарным, если больше критического значения – турбулентым.
Рис. 3.1
Турбулентное течение. При больших скоростях движения и для маловязких жидкостей определяющим является действие инерционных сил, т.е. кинетической энергии на поток. При этом Re > Reкр. Такой режим называется турбулентным. Здесь имеют место поперечные пульсации и перемешивание частиц жидкости по сечению потока, а также сглаживание эпюры скоростей. Для турбулентного потока характерны: логарифмический закон изменения скорости жидкости по сечению трубы (притупленная эпюра скорости – рис. 3.1, б – по сравнению с параболической; закон сопротивления, близкий к квадратичному 2, влияние шероховатости стенок на коэффициент путевых потерь (особенно при больших числах Re). Для таких чисел Re в уравнении Бернулли (формула 2.1) коэффициент Кориолиса может быть принят равным 1.
Подкрашенная струйка жидкости, поступившая в приосевую область потока, сразу же размывается по всему сечению (рис. 3.2, б).
Описание экспериментальной установки
Схема установки представлена на рис. 3.2. Основными элементам ее являются – бак с водой 1, стеклянная труба 2 и бачок с подкрашенной жидкостью 5. Краном 3 изменяется расход воды через трубу. Мерная емкость 4 и секундомер 8 позволяют измерять расход. Краник 6 и насадок 7 обеспечивают поступление подкрашенной струйки жидкости в трубу.
Рис. 3.2
Порядок выполнения работы
Перед началом опыта необходимо наполнить бак 1 водой и проверить наличие красителя в бачке 5.
Приоткрыть кран 3 и установить небольшой расход воды по трубе 2. Одновременно отрегулировать подачу красителя краником 6 через насадок 7 так, чтобы струйка красителя была достаточно тонкой и хорошо видимой. Визуально наблюдать характер перемещения струйки.
Помещая мерную емкость 4 под срез трубы, одновременно включить секундомер 8 и засечь время наполнения емкости до определенной отметки (например, до 1 л). Это позволяет измерить расход Q жидкости и ее среднюю скорость
.Повторить операции по пп. 2, 3 при большем открытии крана 4 (не закрывая его).
Проделать те же операции еще 1-2 раза, установив такие расходы, при которых режим течения будет турбулентным, т.е. такой режим, при котором струйка красителя будет интенсивно размываться.
По данным измерений определить величины чисел Re, сопоставить их с критическими значениями и результатами визуальных наблюдений.
Составить отчет по лабораторной работе на отдельном листе или специальном бланке, занеся в него:
- схему установки и эскизы визуальных наблюдений;
- расчетные формулы (3.1); (2.4); (2.3);
- данные опытов и результаты их обработки с заключением о режимах течения.
Контрольные вопросы
Общие закономерности ламинарного и турбулентного режимов течения: характер течения, профиль скоростей, закон сопротивления, коэффициенты Кориолиса.
Смысл и характерные величины чисел Рейнольдса.
Уравнение расхода. Способы определения расхода.
Уравнение энергии (Бернулли) для потоков жидкости.
Принцип действия установки по изучению режимов течения жидкости.
Рекомендуемая литература
[1, с. 62-69, 75-86, 95-96]. [3, с. 59-63, 67-76].