Лабораторная Работа № 2 опытная проверка уравнения бернулли

Цель работы:

Опытная проверка уравнения энергии (Бернулли) для реальной жидкости при ее течении в трубе переменного сечения.

В работе необходимо:

- измерить давление (с помощью пьезометров) в характерных точках трубы при установившемся движении воды с постоянным расходом;

- построить опытную пьезометрическую линию и линию изменения составляющих напора вдоль трубы.

Основные теоретические положения

Уравнение Бернулли – основное уравнение гидравлики – отражает общий закон сохранения и превращения энергии. Для гидромеханической (ньютоновской) жидкости это уравнение является решением системы дифференциальных уравнений движения и записывается либо для единицы веса (для 1 ньютона), либо для единицы массы (для 1 килограмма), т.е. представляет собой сумму удельных энергий жидкости. Для реальной (вязкой) несжимаемой жидкости при ее установившемся движении это уравнение для единицы веса записывается так:

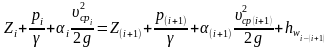, (2.1)

где i – параметры в исходном (для данного рассмотрения) сечении;

(i + 1) – параметры в конечном сечении;

Z – нивелирная высота – высота относительно выбранной горизонтальной плоскости, м;

р – давление, Па;

γ – удельный вес жидкости, Н/м³ ( );

ρ – плотность жидкости, кг/м³;

_cp – средняя скорость, м/с;

 – коэффициент Кориолиса;

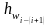– потери напора на рассматриваемом участке, м.

При подсчете этих величин следует иметь в виду, что нивелирная высота Z может отсчитываться от любого уровня, одинакового для всех сечений в данном опыте. Коэффициент  учитывает неточность подсчета кинетической энергии в сечении по среднеарифметическому значению скорости. (В данном опыте для воды при развитом турбулентном течении он может быть принят равным единице, см. лабораторную работу № 3).

Легко видеть, что размерность каждого слагаемого в уравнении (см., например, второе слагаемое) получается делением единицы энергии (джоуль) на единицу веса (ньютон). Именно поэтому получается одинаковая размерность всех слагаемых в уравнении Д. Бернулли:

Таким образом каждое слагаемое в уравнении Д. Бернулли отражает одну из составляющих напора (полной удельной энергии) потока реальной жидкости, выраженной в метрах:

Z – энергия положения единицы веса или геометрический напор, м;

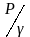– энергия (работа) сил давления единицы веса или пьезометрический напор, м;

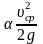– кинетическая энергия единицы веса жидкости или ее скоростной напор, м.

Первые два слагаемых характеризуют потенциальную энергию.

Если все члены уравнения умножить на g (ускорение земного тяготения), то оно будет записано для 1 килограмма массы:

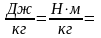м/с².

Уравнение Бернулли показывает, что по мере движения реальной жидкости от сечения к сечению ее полная механическая энергия уменьшается за счет безвозвратных потерь. Безвозвратных, т.к. эти потери образуются за счет трения и превращаются в тепло, а затем – рассеиваются в окружающем пространстве. Для установившегося движения в потоке постоянного сечения это проявляется в уменьшении давления в направлении движения жидкости.

Для потока идеальной (невязкой) жидкости этих потерь нет, не изменяется за счет трения и скорость по сечению потока, поэтому уравнение Бернулли отряжает постоянство напора H и получается из уравнения (2.1) при условиях 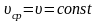; α = 1; = 0:

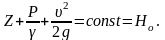(2.2)

здесь Н_о – начальная удельная энергия – высота положения уровня воды в пьезометрах над контрольной горизонтальной плоскостью (с учетом Z) до открытия крана (см. рис. 2.1).

Для реальной жидкости средняя скорость _cp в любом сечении потока с площадью F может быть определена из уравнения расходов:

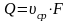, (2.3)

здесь Q – объемный расход жидкости, м³/с.

Объемный расход Q, м³/с может быть подсчитан по опытному значению объема жидкости W в м³, поступившей за время t, с:

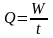, м³/с. (2.4)

Объем W можно определить и по удельному весу  , Н/м³ по формуле:

, м³. (2.5)

Термин «объемный» часто опускают, хотя существует еще массовый расход

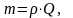кг/с.

Следует иметь в виду, что при весовом определении расхода в кгс/с необходимо предварительно его перевести в ньютоны, умножением на g.

По результатам определения составляющих уравнения Бернулли (2.1) можно графически построить изменение пьезометрического напора по сечениям – пьезометрическую линию. Она является отображением высоты столбов жидкости в пьезометрах (см. формулу 1.2). Можно также отложить величины остальных составляющих напора Z_i и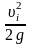 . Безвозвратные потери напора 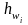на участках между пьезометрами можно определить из равенства, отражающего закон сохранения и превращения энергии:

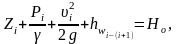м. (2.6)

Рис. 2.1

Это изображение называется графической интерпретацией уравнения Бернулли (см. рис. 2.1). Реальный напор в каждом сечении отражается пунктирной линией, потенциальная энергия – пьезометрической линией.

Описание экспериментальной установки

Основной элемент установки (рис. 2.2) – горизонтальная труба переменного сечения с пьезометрами. Вода в нее поступает из напорного бака.

Рис. 2.2

До открытия вентиля В1 высота воды в пьезометрах соответствует уровню Н_о. После его открытия через некоторое время колебаний уровней устанавливается течение воды по трубе. Расход воды измеряется весовым способом с помощью специальной емкости, весов и секундомера. Уровень в баке остается практически постоянным и равным Н_о, скорость жидкости в нем близка к нулю. Поэтому измерение уровня Н_Б в баке по пьезометру Б дает значение начального напора Н_о в м.вод.ст., т.е. Н_Б = Н_о.

Порядок выполнения работы

1. Вычертить схему установки (рис. 2.2) на специальном бланке или на отдельном листе, записать расчетные соотношения 2.1, 2.3, 2.4, 2.5 и величины диаметров на участках трубы.

2. Полностью открыть вентиль В1 и дождаться, пока исчезнут колебания уровней воды и установится неизменный расход воды на слив.

3. После установления неизменного расхода, одновременно:

- отсчитать показания всех пьезометров от оси трубы;

- к концу трубы подставить мерную емкость и определить вес G жидкости, поступившей в нее за время t.

4. Опыт (со взвешиванием, отсчетами по пьезометрам и секундомеру) повторить второй раз.

5. По данным двух опытов подсчитать средние вес, объем воды, время и секундный расход по формулам (2.4) и (2.5).

6. Рассчитать площади F_i круглых сечений трубы на участках и определить по формуле (2.3) среднюю скорость на каждом участке.

7. Подсчитать в каждом сечении все слагаемые уравнения Бернулли (2.1), причем величина Z должна отсчитываться от любого (но одинакового для всех сечений) уровня до оси трубы.

8. Построить график изменения удельной энергии жидкости по сечениям в масштабе для оси ординат (для оси абсцисс масштаб выдерживать не обязательно).

9. Определить величину безвозвратных потерь напора 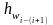между точками установки пьезометров по формуле (2.6).

Контрольные вопросы

1. Жидкость как гидромеханическое понятие. Виды жидкостей. Основные свойства гидромеханических (ньютоновских) жидкостей и характеризующие их параметры (плотность, удельный вес, коэффициенты вязкости).

2. Уравнение Бернулли для идеальной и реальной жидкости. Его физическая интерпретация. Смысл всех величин и слагаемых. Размерности.

3. Геометрическая интерпретация уравнения Бернулли для реальной жидкости. Изменения составляющих напора.

4. Уравнение движения (Эйлера) для идеальной жидкости. Смысл входящих в него величин.

5. Уравнение расхода. Способы определения расхода.

6. Принцип действия установки по проверке уравнения Бернулли, способы измерения давления и расхода жидкости в опытах.

Рекомендуемая литература

[1, с. 40-55, 8-16]. [2, с. 349, 433-434]. [3, с. 41-51, 12-18].