
Решение РГЗ Вариант 18
.docМИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
ЛИПЕЦКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
КАФЕДРА ВЫСШЕЙ МАТЕМАТИКИ
Расчетно-графическое задание
по дисциплине
«Теория вероятности»
|
|
Студент |
|
|
|
Филатов А.А. |
|
||||||||
|
|
|
|
подпись, дата |
|
фамилия, инициалы |
|
||||||||
|
|
Группа |
|
АС-09 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
||||||||
|
|
Принял |
|
|
|
|
|
||||||||
|
|
|
|
|
|
Денисенко Ю.И. |
|
||||||||
|
|
ученая степень, звание |
|
подпись, дата |
|
фамилия, инициалы |
|
||||||||
Липецк 2011
Вариант 18
Таблица 1 – Выборка для задания №1
|
X |
-2,25 |
-2,00 |
-1,75 |
-1,50 |
-1,25 |
-1,00 |
-0,75 |
-0,50 |
-0,25 |
0,00 |
|
Y |
-26,49 |
-19,86 |
-17,28 |
-12,65 |
-11,84 |
-7,99 |
-7,77 |
-6,29 |
-5,51 |
-4,95 |
|
X |
0,25 |
0,50 |
0,75 |
1,00 |
1,25 |
1,50 |
1,75 |
2,00 |
2,25 |
2,50 |
|
Y |
-4,56 |
-3,97 |
-4,43 |
-2,21 |
-2,33 |
-0,18 |
-0,16 |
3,19 |
5,14 |
9,96 |
Таблица 2 – Выборка для задания №2
|
Y \ X |
12,5 |
13,5 |
14,5 |
15,5 |
16,5 |
17,5 |
18,5 |
|
22,5 |
0 |
0 |
0 |
0 |
0 |
2 |
1 |
|
23,5 |
0 |
0 |
0 |
1 |
2 |
8 |
0 |
|
24,5 |
0 |
0 |
0 |
4 |
17 |
6 |
0 |
|
25,5 |
0 |
0 |
6 |
22 |
6 |
0 |
0 |
|
26,5 |
0 |
4 |
21 |
11 |
0 |
0 |
0 |
|
27,5 |
0 |
4 |
1 |
0 |
0 |
0 |
0 |
|
28,5 |
1 |
3 |
0 |
0 |
0 |
0 |
0 |
1. Обработка выборки №1
Вычислим числовые характеристики выборки:
![]()
![]()
![]() ;
;
![]()
![]() ;
;
![]()
![]()
![]()
Поле корреляции представлено на следующем рисунке:
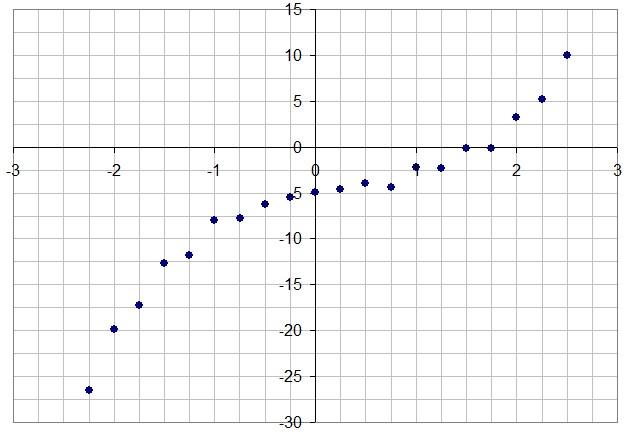
Предположим, что X и Y связаны функциональными зависимостями вида:
1)
![]()
2)
![]() .
.
Определим параметры зависимости вида (1):
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
-2,250 |
5,063 |
-11,391 |
25,629 |
-57,665 |
129,746 |
-26,490 |
59,602 |
-134,106 |
301,737 |
|
2 |
-2,000 |
4,000 |
-8,000 |
16,000 |
-32,000 |
64,000 |
-19,860 |
39,720 |
-79,440 |
158,880 |
|
3 |
-1,750 |
3,063 |
-5,359 |
9,379 |
-16,413 |
28,723 |
-17,280 |
30,240 |
-52,920 |
92,610 |
|
4 |
-1,500 |
2,250 |
-3,375 |
5,063 |
-7,594 |
11,391 |
-12,650 |
18,975 |
-28,462 |
42,693 |
|
5 |
-1,250 |
1,563 |
-1,953 |
2,441 |
-3,052 |
3,815 |
-11,840 |
14,800 |
-18,500 |
23,125 |
|
6 |
-1,000 |
1,000 |
-1,000 |
1,000 |
-1,000 |
1,000 |
-7,990 |
7,990 |
-7,990 |
7,990 |
|
7 |
-0,750 |
0,563 |
-0,422 |
0,316 |
-0,237 |
0,178 |
-7,770 |
5,8275 |
-4,370 |
3,277 |
|
8 |
-0,500 |
0,250 |
-0,125 |
0,063 |
-0,031 |
0,016 |
-6,290 |
3,145 |
-1,572 |
0,786 |
|
9 |
-0,250 |
0,063 |
-0,016 |
0,004 |
-0,001 |
0,000 |
-5,510 |
1,377 |
-0,3443 |
0,086 |
|
10 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
-4,950 |
0,000 |
0,00 |
0,00 |
|
11 |
0,250 |
0,063 |
0,016 |
0,004 |
0,001 |
0,000 |
-4,560 |
-1,140 |
-0,285 |
-0,071 |
|
12 |
0,500 |
0,250 |
0,125 |
0,063 |
0,031 |
0,016 |
-3,970 |
-1,985 |
-0,992 |
-0,496 |
|
13 |
0,750 |
0,563 |
0,422 |
0,316 |
0,237 |
0,178 |
-4,430 |
-3,322 |
-2,491 |
-1,869 |
|
14 |
1,000 |
1,000 |
1,000 |
1,000 |
1,000 |
1,000 |
-2,210 |
-2,210 |
-2,210 |
-2,210 |
|
15 |
1,250 |
1,563 |
1,953 |
2,441 |
3,052 |
3,815 |
-2,330 |
-2,912 |
-3,640 |
-4,551 |
|
16 |
1,500 |
2,250 |
3,375 |
5,063 |
7,594 |
11,391 |
-0,180 |
-0,270 |
-0,405 |
-0,608 |
|
17 |
1,750 |
3,063 |
5,359 |
9,379 |
16,413 |
28,723 |
-0,160 |
-0,280 |
-0,490 |
-0,858 |
|
18 |
2,000 |
4,000 |
8,000 |
16,000 |
32,000 |
64,000 |
3,190 |
6,380 |
12,760 |
25,520 |
|
19 |
2,250 |
5,063 |
11,391 |
25,629 |
57,665 |
129,746 |
5,140 |
11,565 |
26,021 |
58,548 |
|
20 |
2,500 |
6,250 |
15,625 |
39,063 |
97,656 |
244,141 |
9,960 |
24,900 |
62,250 |
155,625 |
|
∑ |
2,500 |
41,875 |
15,625 |
158,852 |
97,656 |
721,877 |
-120,180 |
212,402 |
-237,189 |
860,217 |
Составим систему для определения параметров зависимости:
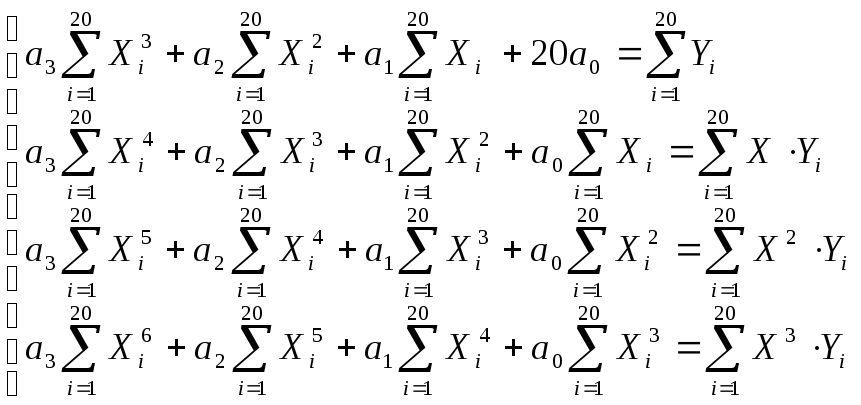


Таким образом, функциональная зависимость (1) имеет вид:
![]()
Определим параметры
зависимости вида (2). Полагаем
![]() .
.
-
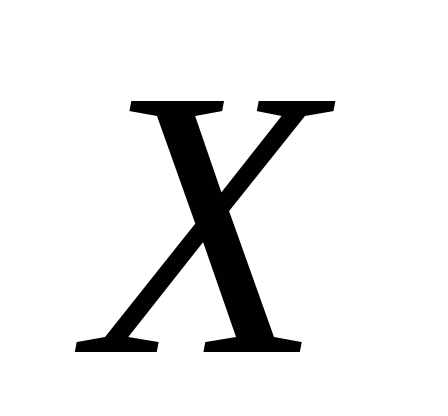

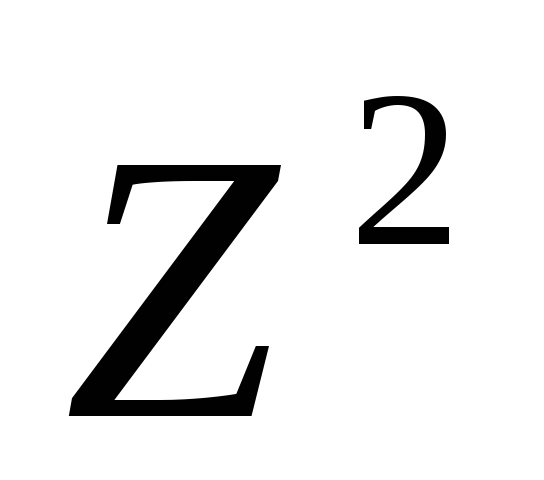

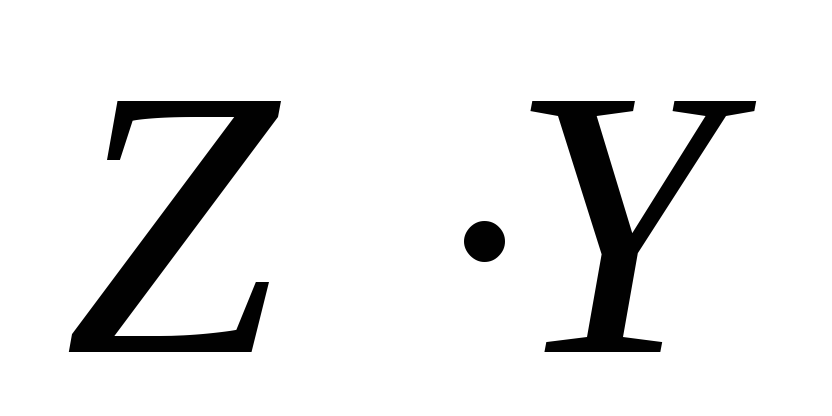
1
-2,250
-9,290
86,309
-26,490
246,100
2
-2,000
-6,695
44,819
-19,860
132,957
3
-1,750
-4,813
23,161
-17,280
83,161
4
-1,500
-3,443
11,856
-12,650
43,557
5
-1,250
-2,441
5,957
-11,840
28,899
6
-1,000
-1,698
2,885
-7,990
13,570
7
-0,750
-1,137
1,293
-7,770
8,834
8
-0,500
-0,697
0,485
-6,290
4,383
9
-0,250
-0,331
0,109
-5,510
1,822
10
0,000
0,000
0,000
-4,950
0,000
11
0,250
0,331
0,109
-4,560
-1,508
12
0,500
0,697
0,485
-3,970
-2,766
13
0,750
1,137
1,293
-4,430
-5,037
14
1,000
1,698
2,885
-2,210
-3,753
15
1,250
2,441
5,957
-2,330
-5,687
16
1,500
3,443
11,856
-0,180
-0,620
17
1,750
4,813
23,161
-0,160
-0,770
18
2,000
6,695
44,819
3,190
21,356
19
2,250
9,290
86,309
5,140
47,752
20
2,500
12,876
165,786
9,960
128,243
∑
2,500
12,876
519,535
-120,180
740,492
Составим систему для определения параметров зависимости:
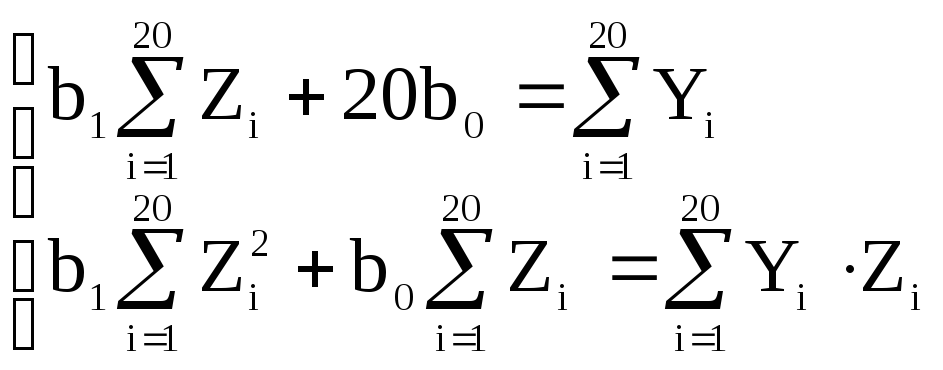
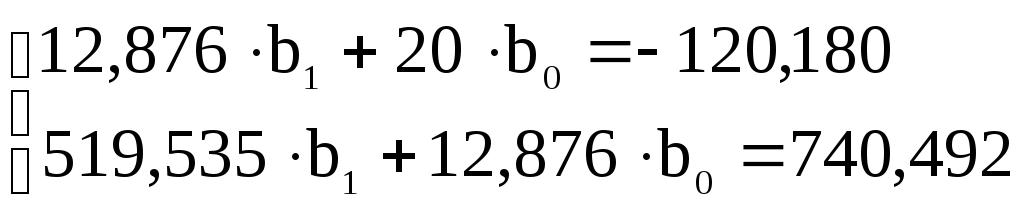
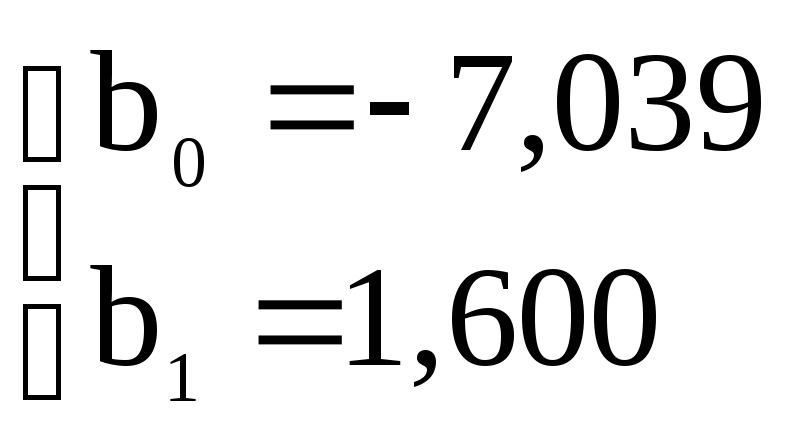
Таким образом,
![]() .
.
Графики зависимостей вместе с точками выборки представлены на рисунке:
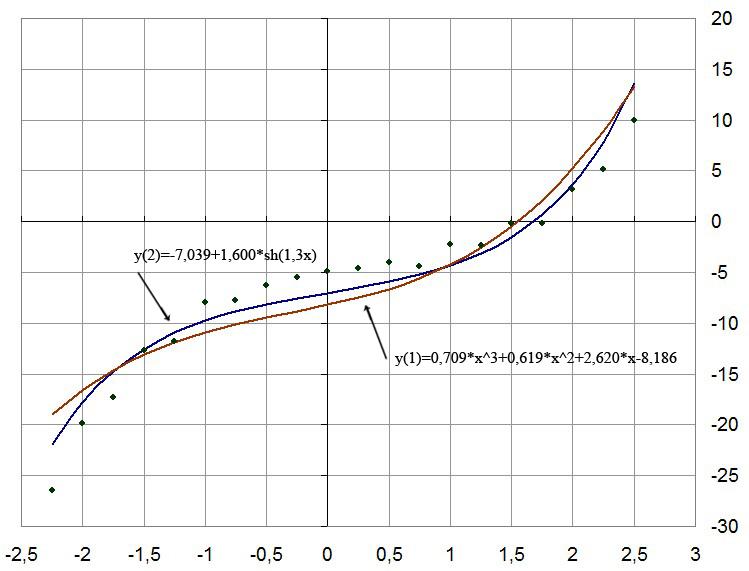
Определим, какая функция лучше аппроксимирует выборку.
|
|
|
|
|
|
|
|
|
1 |
-2,250 |
-19,023 |
-21,903 |
-26,49 |
7,467 |
4,587 |
|
2 |
-2,000 |
-16,622 |
-17,751 |
-19,86 |
3,238 |
2,109 |
|
3 |
-1,750 |
-14,675 |
-14,739 |
-17,28 |
2,605 |
2,541 |
|
4 |
-1,500 |
-13,116 |
-12,548 |
-12,65 |
0,466 |
0,102 |
|
5 |
-1,250 |
-11,879 |
-10,944 |
-11,84 |
0,039 |
0,896 |
|
6 |
-1,000 |
-10,896 |
-9,756 |
-7,99 |
2,906 |
1,766 |
|
7 |
-0,750 |
-10,102 |
-8,858 |
-7,77 |
2,332 |
1,088 |
|
8 |
-0,500 |
-9,430 |
-8,154 |
-6,29 |
3,140 |
1,864 |
|
9 |
-0,250 |
-8,813 |
-7,568 |
-5,51 |
3,303 |
2,058 |
|
10 |
0,000 |
-8,186 |
-7,039 |
-4,95 |
3,236 |
2,089 |
|
11 |
0,250 |
-7,481 |
-6,510 |
-4,56 |
2,921 |
1,950 |
|
12 |
0,500 |
-6,633 |
-5,924 |
-3,97 |
2,663 |
1,954 |
|
13 |
0,750 |
-5,574 |
-5,220 |
-4,43 |
1,144 |
0,790 |
|
14 |
1,000 |
-4,238 |
-4,322 |
-2,21 |
2,028 |
2,112 |
|
15 |
1,250 |
-2,559 |
-3,134 |
-2,33 |
0,229 |
0,804 |
|
16 |
1,500 |
-0,470 |
-1,530 |
-0,18 |
0,290 |
1,350 |
|
17 |
1,750 |
2,094 |
0,661 |
-0,16 |
2,254 |
0,821 |
|
18 |
2,000 |
5,202 |
3,673 |
3,19 |
2,012 |
0,483 |
|
19 |
2,250 |
8,919 |
7,825 |
5,14 |
3,779 |
2,685 |
|
20 |
2,500 |
13,311 |
13,562 |
9,96 |
3,351 |
3,602 |
|
∑ |
--- |
--- |
--- |
--- |
49,403 |
35,651 |
