9.3. Прийняття управлінських рішень щодо оптимального використання ресурсів за умов обмежень

Для оптимізації виробничої програми підприємства необхідно аналізувати не лише інформацію про витрати та їх поділ на постійні і змінні, а й зважати на інші фактори, що впливають на розмір прибутку.

Кожне підприємство у своїй діяльності постійно відчуває якийсь дефіцит, що обмежує його можливості. Це може бути недостатнє забезпечення матеріальними ресурсами (сировиною), виробничими потужностями, попитом на продукцію, чисельністю та кваліфікацією робочої сили, наявністю обігових коштів і т. ін. Діючи в таких умовах, підприємство повинно обирати ті види діяльності, які є найвигіднішими за наявного дефіциту ресурсів, та забезпечити їх повне і ефективне використання.

Рішення про оптимальне використання обмежених ресурсів – це рішення, спрямоване на складання такої виробничої програми підприємства, яка забезпечить йому отримання максимального прибутку за умов існування обмежень виробництва і реалізації продукції.

Можливості підприємства найчастіше обмежені. Обмеження – це чинники, що обмежують виробництво або реалізацію продукції(послуг).

Прикладами обмежень є попит на продукцію, робоча сила, матеріальні ресурси, виробнича потужність, грошові кошти тощо.

Діючи за умов існуючих обмежень, підприємство змушене обирати ті види продукції або послуг, виробництво яких найвигідніше.

Приймаючи управлінські рішення, потрібно враховувати кількість обмежень. За наявності тільки одного обмеження аналіз інформації для прийняття рішення про оптимальне використання ресурсів підприємства ґрунтується на обчисленні показника маржинального доходу на одиницю обмежувального фактора (рис. 9.3).

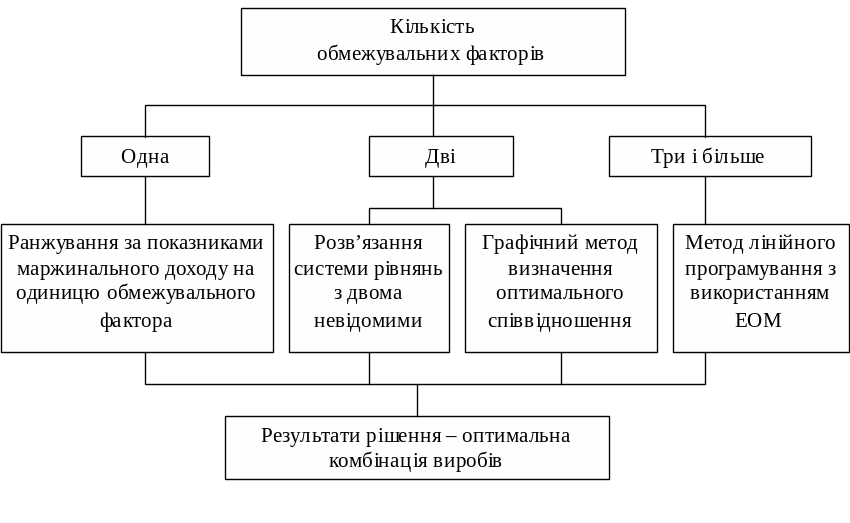
Рис. 9.3 Методи оптимізації виробництва при різній кількості обмежувальних факторів

Аналіз для прийняття рішень залежить від кількості обмежень.

1. Аналіз для прийняття рішення за наявності одного обмеження.

За наявності лише одного обмеження аналіз заради оптимального використання ресурсів підприємства базується на показнику маржинального доходу на одиницю обмежувального фактора – показник, виражений в одиницях обмежувального фактора (машино-годинах, людино-годинах, одиницю сировини, одиницю потужностітощо).

При розподілі обмежених ресурсів слід зважати й на якісні чинники. Зокрема, якщо підприємство не забезпечить мінімальної потреби своїх клієнтів у всіх видах продукції або послуг, воно може втратити частину своїх постійних клієнтів, що, в свою чергу, призведе до скорочення обсягу продажу.

Формування оптимальної виробничої програми при цьому здійснюється поетапно:

1) визначається маржинальний дохід на одиницю обмежувального фактора;

2) проводиться ранжування видів діяльності за рівнем доходності, визначеному на першому етапі;

3) визначається оптимальна програма діяльності з урахуванням обмежувального чинника.

Приклад 9.4

Підприємство може використати максимум 20000 машино-годин роботи обладнання для випуску двох видів продукції А і Б, попит на яку становить 5000 і 3000 одиниць. Ціна реалізації одного виробу А – 20 грн., виробу Б – 30 грн., змінні витрати на одиницю продукції складають відповідно 14 і 22 грн., а витрати машинного часу – 3 і 5 машино-годин. Для виробництва обох видів продукції використовують однакові матеріали. Кваліфікованою робочою силою підприємство забезпечене повністю. Необхідно визначити оптимальну структуру виробництва, яка забезпечить максимальну суму прибутку, якщо це не вплине на зміну суми постійних витрат.

Спочатку визначимо маржинальний дохід:

а) на одиницю виміру:

– продукції А 20 – 14 = 6 грн.;

– продукції Б 30 – 22 = 8 грн.

б) на одну машино-годину (обмежувальний фактор):

– продукції А 6 грн. : 3 машино-години = 2 грн.;

– продукції Б 8 грн. : 5 машино-годин = 1,6 грн.

За останнім показником більш вигідним є виробництво продукції А, тому його обсяг плануємо для повного задоволення попиту – 5000. На такий обсяг виробництва буде використано:

5000 од. × 3 машино-години = 15000 машино-годин.

Отже, для виробництва продукції Б можна буде використати:

20000 – 15000 = 5000 машино-годин,

або запланувати випуск продукції Б в розмірі:

5000 машино-годин : 5 машино-годин = 1000 одиниць

Таким чином, оптимальним буде виробництво 5000 одиниць продукції А і 1000 одиниць продукції Б, що забезпечить максимальну суму маржинального доходу в умовах існуючого обмеження – 38000 грн.:

5000 одиниць × 6 грн. = 30000 грн. (по продукції А),

1000 одиниць × 8 грн. = 8000 грн. (по продукції Б).

При аналізі використання обмеженої кількості ресурсів необхідно також враховувати потреби мінімального забезпечення попиту з усіх видів продукції або дотримання обов’язкового асортименту.

2. Аналіз для прийняття рішення за умов кількох обмежень.

За наявності кількох обмежень аналіз здійснюють за допомогою лінійного програмування – математичного методу, використовуваний для оптимізації виробничої діяльності шляхом розв’язання серії наявних рівнянь лінійних обмежень. Процес лінійного програмування має три стадії: 1) складання рівняння цільової функції та рівнянь обмежень; 2) розв’язання моделі симплексним методом або на ЕОМ з використанням стандартних програм оптимізації; 3) аналіз одержаного рішення.

Побудова моделі лінійного програмування передбачає визначення: 1) змінних величин; 2) цільової функції та побудову її рівняння; 3) обмежень та побудову їх рівнянь.

Цільова функція – мета, якої намагається досягти менеджер.

Рівняння цільової функції – алгебраїчне зображення мети, якої намагається досягти менеджер у процесі лінійного програмування.

Рівняння обмеження – алгебраїчне зображення одного з обмежувальних чинників.

Метою аналізу одержаного рішення є визначення чутливості моделі до зміни значення обмежувальних чинників, тобто визначення, на скільки знизиться значення цільової функції при зменшенні одного з обмежувальних чинників на одиницю його вимірювання. Всебічний аналіз дає можливість зробити обґрунтовані висновки і прийняти правильне управлінське рішення.

На практиці моделі лінійного програмування розв'язують переважно за допомогою комп'ютера. При цьому, залежно від кількості змінних у рівнянні цільової функції можна застосовувати різні методи вирішення.

Графічний підхід до вирішення моделі лінійного програмування означає побудову графіка, в якому осі координат відображають значення змінних величин, і вже за графіком − визначення зони можливих рішень.

Зона можливих рішень − площа графіка лінійного програмування, окреслена лініями рівнянь наявних обмежень.

Для окреслення зони можливих рішень насамперед необхідно визначити координати ліній обмежень.

Оптимальна комбінація виробів − це завжди кут зони можливих рішень.

Розв'язання шляхом спроб і помилок передбачає послідовне підставляння координат кожного кута зони можливих рішень у рівняння цільової функції. Спроба, яка покаже найбільше значення показника цільової функції, означає оптимальну комбінацію.

Альтернативний шлях знаходження оптимального кута передбачає використання рівно економічних рішень. Для цього на графіку проводять лінію цільової функції, яка перетинає зону можливих рішень побудови і використання ліній рівно економічних рішень.

Метою аналізу вирішення є визначення чутливості моделі до зміни значень обмежувальних чинників. Для цього обчислюють тіньову ціну.

Тіньова ціна − величина зниження значення цільової функції внаслідок зменшення значення відповідного обмежувального чинника на одну одиницю.

При наявності двох обмежень аналіз можна виконати шляхом побудови та розв’язання системи лінійних рівнянь з двома невідомими або графічним методом.

Приклад 9.5

Завод виготовляє два види продукції (А і Б), яка проходить послідовну обробку у двох цехах (№ 1 і № 2). Потужність кожного цеху обмежена кількістю машино-годин роботи обладнання: цех № 1 – 1780 годин, цех № 2 – 1160 годин. Затрати машинного часу на одиницю продукції розподіляються таким чином:

– продукція А: цех № 1 – 5 годин, цех № 2 – 4 години;

– продукція Б: цех № 1 – 8 годин, цех № 2 – 2 години.

Маржинальний дохід на одиницю продукції А – 54 грн., продукції Б – 75 грн.

Необхідно визначити оптимальний обсяг виробництва окремих видів продукції за наявних обмежень.

Д ля розв’язання задачі складемо рівняння витрат машинного часу по цехах:

№ 1 5х₁ + 8х₂ = 1780

№ 2 4х₁ + 2х₂ = 1160 ,

де х₁ – обсяг виробництва продукції А;

х₂ –обсяг виробництва продукції Б.

Розв’яжемо цю систему рівнянь звичайним алгебраїчним методом: поділимо почленно перше рівняння на 5, а друге – на 4 та віднімемо друге рівняння від першого:

х₁ + 1,6х₂ = 356

х₁ + 0,5х₂ = 290

1,1х₂ = 66

х₂ = 60

х₁ + 0,5 × 60 = 290

х₁ = 290 – 30

х₁ = 260

Отже, підприємству доцільно виготовляти 260 одиниць продукції А та 60 одиниць продукції Б, що забезпечить повне використання машинного часу:

цех № 1 5 × 260 + 8 × 60 = 1780,

цех № 2 4 × 260 + 2 × 60 = 1160

та принесе підприємству 18540 грн. маржинального доходу:

260 × 54 + 60 × 75 = 18540 грн.