2.6. Специфічні механізми планування

Дослідження механізмів планування процесу функціонування організаційної системи показало, що задача вибору оптимального механізму керування назагал є вельми складною. Разом із тим ми переконалися, що механізм відкритого керування оптимальний. За цим механізмом у ситуації рівноваги сповіщається достовірна інформація і реалізація збігається з планом. Зокрема, було показано, що оптимальний механізм існує в системах з повною централізацією планування, хоча задача його конструктивного визначення не вирішена назагал, наприклад, якщо повна централізація в системі неприпустима за деякими причинами. У зв’язку з цим важливо розглянути можливі специфічні механізми планування.

Із теорії оптимального планування відомо, що задача планування процесу функціонування будь-якої економічної системи є оптимізаційною. Але кожна конкретна постановка такої задачі вимагає пошуку спеціального методу її розв’язання, що потребує наявності різних механізмів планування.

Позначимо, як і раніше, через оцінку параметра , що сповіщає і-тий виконавець GB, а через — сукупність усіх оцінок.

На підставі отриманої інформації GB визначає виконавцям плани { } і ціну одиниці продукції.

Процедуру визначення планів і ціни називають механізмом керування ( — механізм планування, — механізм ціноутворення). Механізми керування визначають зазвичай на підставі відповідних принципів керування.

У детермінованій задачі оптимального планування максимізують або мінімізують цільову функцію ОС за деяких обмежень. При цьому неявно передбачають, що план, отриманий у результаті вирішення задачі, може бути реалізований, тобто y = x. За цих умов модель цієї задачі матиме вигляд

.

Механізм жорсткого планування. Розвитком процедури оптимального планування є принцип жорсткої централізації, за яким виконавці мають свободу вибору, а GB у першу чергу враховує інтереси системи. Цей принцип відповідає вирішенню керівним органом оптимізаційної задачі

.

Оптимальне рішення задачі визначає механізм планування

.

Механізм ціноутворення обирають довільно, а його конкретизація визначає певний механізм жорсткої централізації.

Приймаючи ціну фіксованою і перетворюючи функцію цілі на функцію оцінок

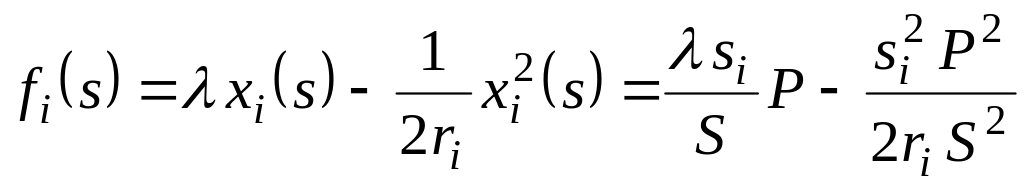, (2.44)

бачимо, що прибуток і-того виконавця залежить як від його оцінки, так і від оцінок інших виконавців. Максимум функції досягається в точці .

У цьому разі аналіз функціонування системи природно здійснювати на підставі теоретико-ігрового підходу, оскільки ми маємо справу з типовою грою n осіб (виконавців) з функціями виграшу і-того гравця (виконавця) . При цьому оцінка є стратегією і-того гравця, відрізок [d, D] — множиною можливих стратегій, а сукупність оцінок — ситуацією гри [31]. Рішенням гри є ситуація рівноваги у розумінні Неша (точка Неша), тобто ситуація , за якої .

Оскільки — зростаюча функція , то при , при , при обов’язково .

Припустимо, що виконавці упорядковані за зростанням , тобто , і розглянемо п’ять можливих варіантів реалізації механізму жорсткого планування.

1. Пропозиції виконавців з обсягів випуску продукції суттєво перевищують попит на неї: тобто , де Р — попит на продукцію У цьому разі існує єдина ситуація рівноваги , при цьому .

2. Пропозиції виконавців з обсягів випуску продукції перевищують попит: .

Визначимо таке, що . Тоді ситуація

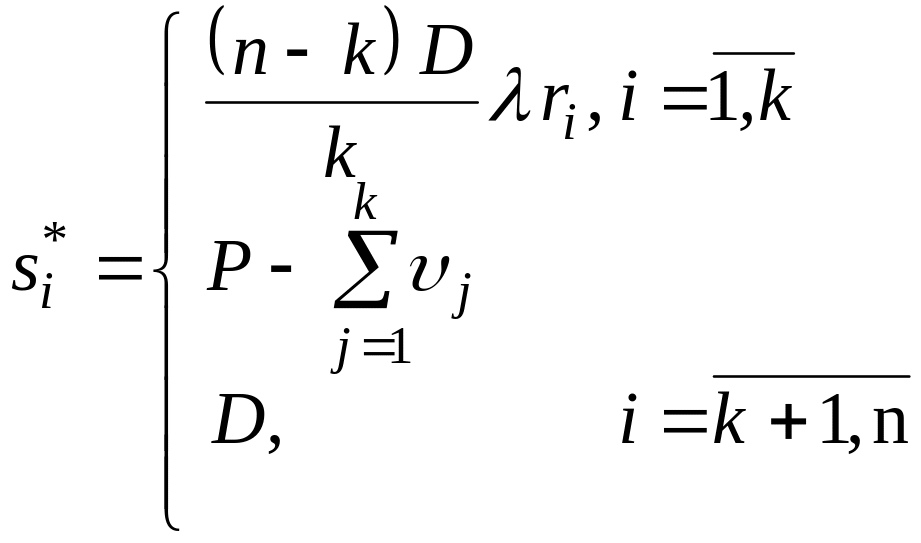(2.45)

є точкою Неша.

Для підтвердження цього висновку доведемо спочатку справедливість нерівності:

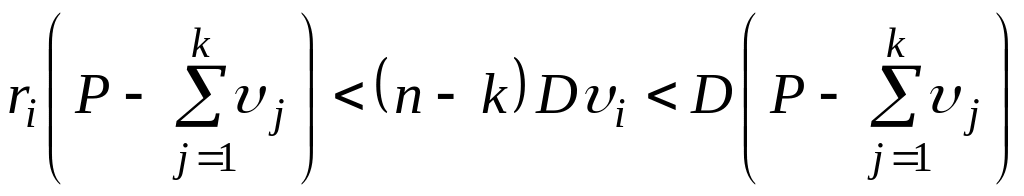, . (2.46)

Права частина нерівності випливає з умови , .

Дійсно, якщо , то , а це суперечить умові вибору k.

Ліва частина нерівності (2.46) випливає з умови .

Отже, для . Разом із тим для , тобто для виконавців з номерами умови рівноваги Неша виконані. Дотримання цих вимог для виконавців із номерами випливає з правила вибору k, оскільки для них справджується умова .

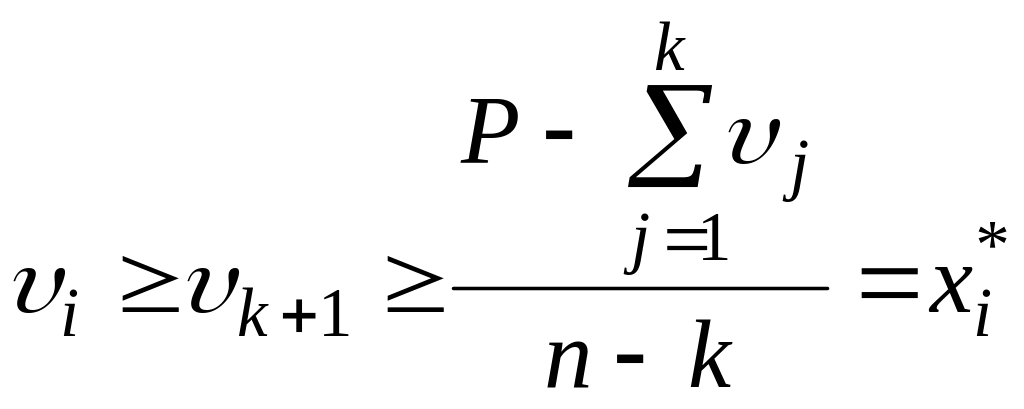Отже, точка (2.45) є єдиною точкою рівноваги.

3. Існує баланс попиту і пропозиції на продукцію: . У цьому разі будь-яка ситуація виду є точкою Неша, оскільки . Можна довести, що лише ця точка буде точкою рівноваги [17].

Враховуючи, що , з умови отримують можливі значення параметра : .

4. Попит на продукцію перевищує пропозицію з боку виконавців: . Визначимо таке, що . Тоді існує єдина точка рівноваги

Доведення проводиться аналогічно випадку 2.

5. Попит на продукцію суттєво перевищує пропозицію з боку виконавців:

. Єдиною ситуацією рівноваги є .

Ефективність механізму жорсткого планування можна підвищити за рахунок введення штрафів за спотворення виконавцями інформації, але й при цьому достовірність оцінок та оптимальність планів можуть бути забезпечені лише за достатньо високої ціни, а саме: , якщо [17].

Механізм відкритого планування. Аналіз механізму жорсткого планування виявив розбіжність інтересів GB і виконавців, яке виникає при , тобто коли не збігається обсяг випуску продукції, що планує GB, з сумарним обсягом, що планують випускати виконавці, користуючись дозволеною їм свободою у наданні інформації GB. Таке неузгоджене планування спричиняє низьку ефективність цього механізму, який виявиться недостатньо ефективним навіть за варіантом 3, коли , тобто коли цілі GB і виконавців збігаються. У цьому разі достатньо встановити ціну . Але GB не знає істинної величини H, йому відомі лише межі її зміни ( ).

Попри зазначене протиріччя можна усунути, використавши відому GB інформацію про оцінки виконавців, а отже, і оцінки величини H, оцінок цільових функцій виконавців як функцій вподобання та оцінок вигідних для виконавців планів . З цією метою задамося механізмом керування

, . (2.47)

Як було показано, за заданим законом керування і-тий виконавець отримує план, що забезпечує максимум його функції вподобання, що відображає уявлення GB про інтереси виконавців. Такий план називають узгодженим, а принцип, за яким він отриманий, — принципом відкритого керування (див. п. 2.1).

У формалізованому вигляді принцип відкритого керування має вигляд:

, (2.48)

, (2.49)

= . (2.50)

Задачу (2.48) — (2.50) називають задачею узгодженого планування, а умови (2.50) — умовами досконалого узгодження.

Для визначення точок рівноваги Неша гри, що відповідає закону відкритого керування, підставимо вираз (2.47) у цільову функцію і-того виконавця:

.

Диференціюючи цю функцію по , маємо n рівнянь

,

після перетворення яких матимемо систему рівнянь для визначення точок рівноваги

, . (2.51)

Якщо рішення даної системи , то — ситуація рівноваги.

Як відомо [17], система рівнянь (2.51) має єдине рішення.

Слід наголосити, що хоча механізм відкритого керування ефективніший за механізм жорсткого керування, за малої кількості виконавців та особливо за наявності в системі монополіста, його ефективність може бути доволі низькою.

Механізм узгодженого планування. Особливостями розглянутих принципів формування механізмів керування (жорсткої централізації і відкритого керування) є те, що вони відображають різні інтереси. Перший із них відображає інтереси GB, оскільки висуває вимогу мінімізації сумарних витрат на випуск продукції, а другий — інтереси виконавців, позаяк у його основі лежить вимога призначення виконавцям тільки найкращих з їхнього погляду планів. Порівняння цих принципів свідчить про певні переваги другого.

Розглянемо задачу планування виробництва продукції, в якій інтереси GB і виконавців збігаються, тобто існує така ціна , за якої плани , що забезпечують максимальні прибутки виконавців, визначають разом із тим і оптимальний план з позиції GB, хоча в загальному випадку їхні інтереси можуть збігатися частково.

Запишемо суму цільових функцій виконавців

.

Перетворивши цільові функції виконавців з урахуванням механізму жорсткої централізації до вигляду

, (2.52)

маємо

,

де .

Якщо розташована в середині [d, D], то система рівнянь для визначення ситуації рівноваги матиме вигляд

, (2.53)

де .

Ця система відрізняється від системи (2.51) лише позначеннями, тому за достатньо великої кількості виконавців , а значить . Звідси випливає еквівалентність механізмів жорсткої централізації і відкритого керування з позицій збігу плану і ціни у відповідних ситуаціях рівноваги. Цей висновок справедливий не тільки для механізму жорсткої централізації, а й для будь-якого механізму вигляду

, (2.54)

який визначають шляхом реалізації моделі

, (2.55)

, (2.56)

, (2.57)

де — строго монотонна і неперервно диференційована функція .

Очевидно, при маємо механізм відкритого керування, а при — механізм жорсткої централізації.

Функція (2.57), аналогічна функції , слугує для вираження уподобань виконавців до різних планів, оскільки своєю оцінкою виконавець інформує GB, що за ціни найкращим для нього планом є той, що забезпечує максимум функції .

Як і раніше, функцію

називатимемо функцією вподобання (переваги), умови (2.57) — умовами узгодження, задачу (2.55) — (2.57) — задачею узгодженого планування, а принцип формування механізмів керування, за яким вирішується задача узгодженого планування, — принципом узгодженого керування.

Конкретний механізм узгодженого керування визначають обранням конкретних функцій уподобання та процедури розв’язання задачі узгодженого планування, якщо воно не єдине. Назагал механізм узгодженого планування можна записати як розв’язання задачі узгодженого планування виду:

,

,

,

.

Еквівалентність всіх механізмів виду (2.52) формулюють як властивість інваріантності механізмів узгодженого керування з функціями у розумінні незалежності рівноважних планів і ціни від виду функцій . Властивість інваріантності має місце як для більш загальних механізмів керування, так і для більш загальних моделей планування [17].

Гіпотеза слабкого впливу. Вище було встановлено, що для механізмів узгодженого керування рівноважний план близький до оптимального. Для пояснення цього факту запишемо умови рівноваги для довільного механізму

,

припускаючи, що рівновага досягається всередині області можливих ситуацій, тобто .

Вважаючи і неперервно диференційованими функціями { }, у результаті диференціювання здобудемо систему рівнянь

, (2.58)

з якої при і маємо

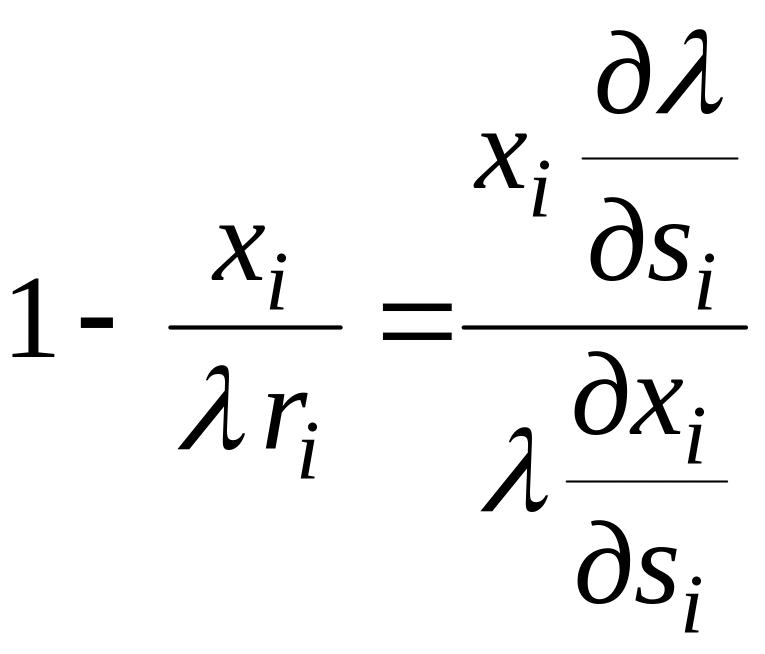. (2.59)

Якщо зі збільшенням n праві частини рівнянь (2.59) наближаються до нуля, то , а оскільки , то , а отже, .

Крім того, як наголошувалося вище, зменшення правих частин рівнянь (2.59) при збільшенні n пов’язано з виконанням умови слабкого впливу:

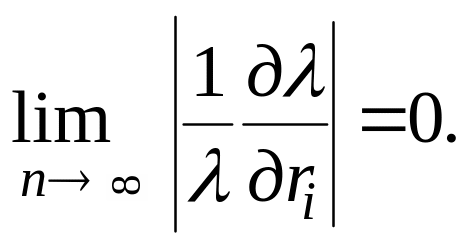
За наявності слабкого впливу в системі доцільною є гіпотеза слабкого впливу, за якою в процесі повідомлення інформації виконавці не враховують її вплив на ціну, оскільки в умовах реального виробництва з його невизначеністю і випадковими збуреннями врахування цього впливу не має практичного сенсу. За цієї гіпотези умови рівноваги будуть відрізнятися від (2.58). Відповідну ситуацію за гіпотези слабкого впливу називають точкою Неша або просто ситуацією рівноваги. Рівняння для її визначення мають вигляд

,

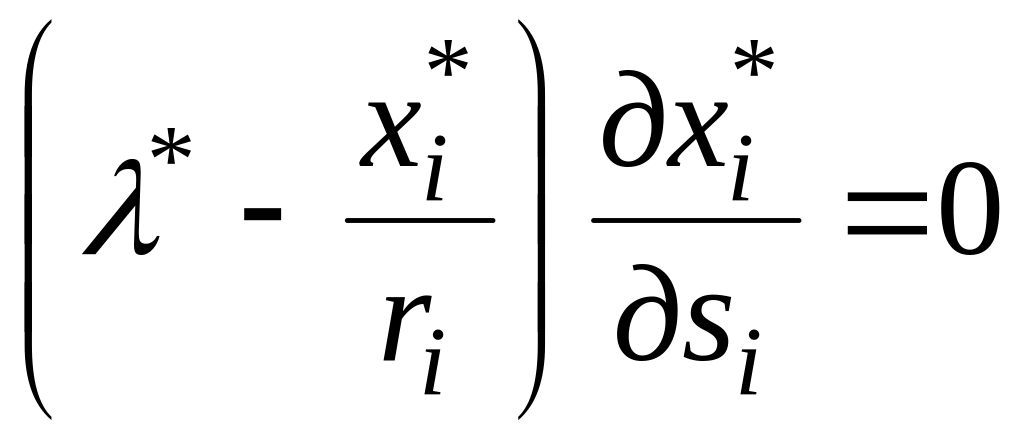з яких з урахуванням одержимо:

.

Отже, будь-якому механізму керування , що задовольняє умовам

, ,

у ситуації рівноваги за гіпотези слабкого впливу існує один і той самий план і ціна . При цьому, як вже наголошувалося, передбачають існування такого рішення системи рівнянь , що .

З умов рівноваги і умов досконалого узгодження ( ) випливає, що за механізмом відкритого керування в ситуації рівноваги за гіпотези слабкого впливу всі виконавці повідомляють достовірні оцінки коефіцієнтів ефективності виробництва. Ця властивість механізму відкритого керування вирізняє його серед інших механізмів керування. Вона є особливо важливою у разі, коли функція системи залежить як від фактичних витрат , так і від планових витрат . Дійсно, за відхилень планових витрат від фактичних система зазнає додаткових втрат, тобто < при . За цих умов оптимальним буде механізм, що забезпечує достовірність інформації, яку повідомляють виконавці, тобто механізм відкритого керування.