2.5. Механізми планування виробничої діяльності

У задачах розподілу і перерозподілу ресурсів функціонування ОС визначалося трьома складовими — способом формування даних, цільовими функціями і процедурами планування, що становили механізм функціонування системи. Розглянемо одну з важливих його характеристик — рівень централізації у процесі планування виробничої діяльності (ціноутворення і випуску продукції). Відсутність санкцій за відхилення реальних показників від планових відповідає децентралізації планування і, навпаки, сильні штрафи відповідають крайньому рівню централізації планування, оскільки в цьому разі реальні показники збігаються з плановими. Проміжні випадки відповідають частковій централізації (децентралізації).

Розглянемо цільову функцію системи у вигляді

, , (2.36)

де — реальні показники (витрати);

— планові показники (витрати).

У разі повної децентралізації планування витрат коефіцієнт набуває нульового значення, тобто тут діють важелі ринкової системи. Якщо ж є безкінечною величиною, то має місце повна централізація планування.

Розглянемо випадок децентралізації планування, коли випуск продукції , тобто коли план або перевиконується, або недовиконується. Тоді цільова функція з урахуванням штрафів за відхилення планових показників від фактичних матиме вигляд

,

а за повної децентралізації планування —

.

У разі децентралізованого планування, коли і-тий виконавець самостійно призначає ціну зі штрафами за її відхилення від ціни GB, цільова функція набуває вигляду

, (2.37)

де .

При 0, тобто коли ціну, обсяг випуску продукції та величину витрат призначає кожен виконавець самостійно, має місце повна децентралізація планування (випадок ринкової системи). У цьому разі функція цілі має вигляд:

.

Сукупність цільових функцій виконавців f= називають системою стимулювання. Розглянемо дві системи і виду (2.37). Якщо , то система має більший рівень централізації, ніж система .

Системи виду (2.37) мають геометричну інтерпретацію (рис. 2.8).

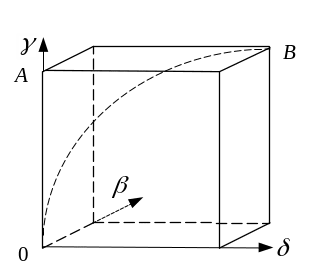
Рис. 2.8. Геометрична інтерпретація систем планування

На рис. 2.8 точка 0 відповідає ринковій системі, точка А — системі з повною децентралізацією планування, точка В — системі з повною централізацією планування, а крива лінія, що з’єднує точки 0 і В, відображає множину систем, упорядкованих за рівнем централізації.

Розглянемо кожну із цих систем планування [17].

Ринкова система планування. Позначимо через P планове завдання організаційної системи з випуску продукції. В умовах ринкової системи планування можливі два випадки: і . У першому з них GB нічого не може вдіяти, оскільки ніяк не впливає на обсяг випуску продукції. У другому разі споживачі, що відіграють роль GB, можуть придбати продукцію за цінами за упорядкованою послідовністю .

Припустимо, що для k-того виконавця існує умова:

.

За цієї умови k — 1 виконавців будуть підвищувати ціни, збільшуючи свій прибуток, а інші n — k виконавців змушені знижувати ціну, звідки випливає, що в рівновазі установиться єдина ринкова ціна продукції . Нехай — випуск продукції і-того виконавця за ринковою ціною. Очевидно, .

Якщо , то, встановлюючи ціну , де — будь-яка мала позитивна величина, і-тий виконавець зможе реалізовувати продукцію в обсязі та отримувати додатковий прибуток. Тому в рівновазі з умови знаходимо

, де .

Оскільки будь-який виконавець спроможний збільшити свій прибуток завдяки установленню ціни при збереженні обсягу випуску , то ситуація не є рівновагою Неша. При цьому інші виконавці можуть збільшити випуск продукції за рахунок призначення ціни , але разом із тим продукція і-того виконавця може й не знайти збуту. Тому при чималій кількості виконавців підвищення ціни зверх не доцільним. За такої умови ситуація буде рівноважною, а випуски продукції — оптимальними.

Визначимо вплив і-того виконавця, який встановив ціну , на ринкову ціну. Очевидно, за такої ситуації всі інші виконавці, встановлюючи ціну , зможуть реалізувати продукцію в обсягах , а і-тий виконавець — лише в обсязі , отримавши прибуток .

Максимум прибутку по становить

.

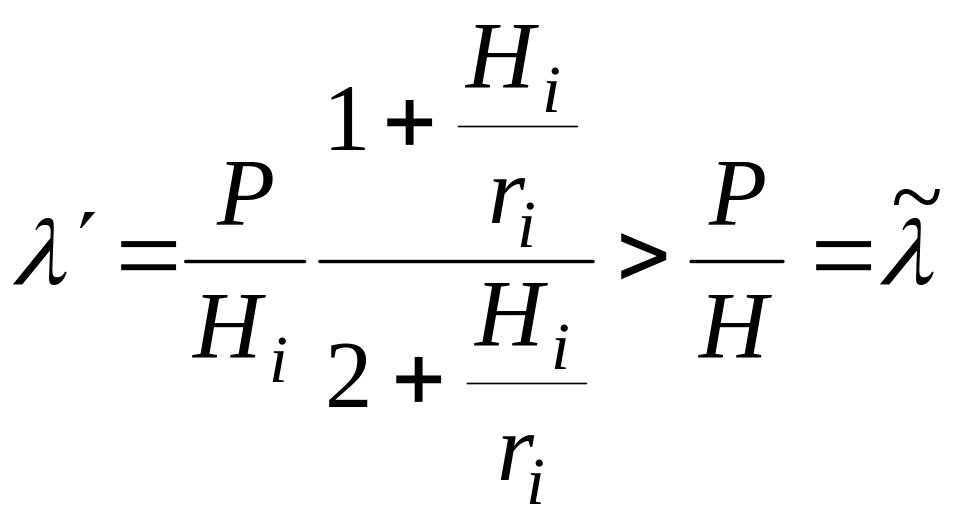У разі присутності виконавця-монополіста, тобто коли , встановлюють монопольну ціна , за якої .

У разі коли попит на продукцію є лінійною функцією ціни, тобто коли , де , при .

Визначимо ціну з умови максимуму прибутку:

.

Диференціюючи цей вираз і виконавши нескладні перетворення, матимемо формулу для визначення ціни:

.

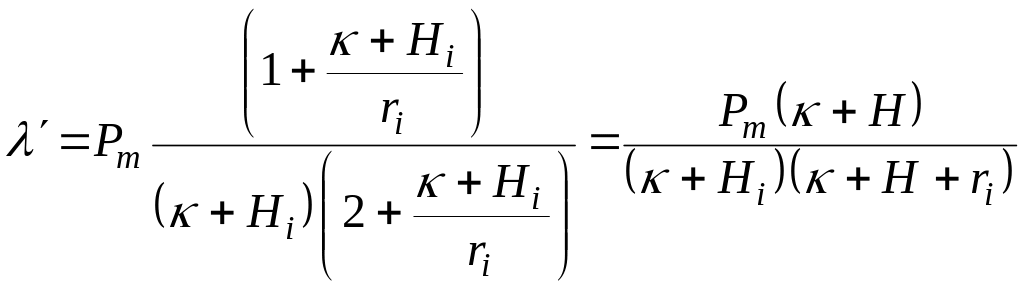Якщо коефіцієнти ефективності всіх виконавців однакові , то маємо

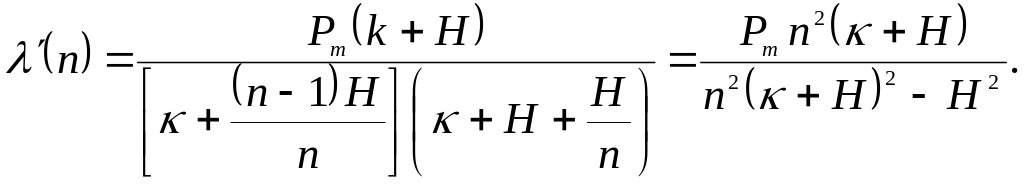
У разі одного виконавця ціну називають монопольною, обчислюючи її за формулою

.

Графік функції наведено на рис. 2.9.

Рис. 2.9. Залежність ціни продукції від кількості виконавців

Повна децентралізація планування. За умов децентралізованого планування виконавці мають право самостійно визначати обсяг випуску продукції, але не мають права на встановлення її ціни. Якщо GB приймає від виконавців усю вироблену продукцію, але при відхиленні її загального обсягу від P у системі виникають втрати, цільова функція GB матиме такий вигляд:

,

де М — достатньо велике число.

Серед способів визначення ціни у системах з повною децентралізацією планування найпростішим є метод «планування за відхиленням», згідно з яким,

якщо в періоді t , то в наступному періоді ціна збільшується, якщо ж

— зменшується. Нехай, наприклад,

,

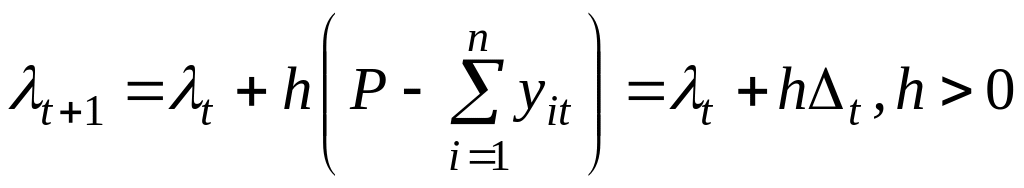де — дефіцит продукції у періоді t.

При < 0 має місце надлишок продукції.

Очевидно, рівновага за гіпотезою слабкого впливу, за якою

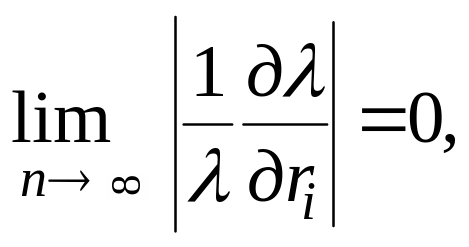
тобто коли зі збільшенням кількості виконавців зменшується вплив окремого виконавця на ціну, визначається співвідношеннями:

або .

Якщо випуск продукції і-тим виконавцем у періоді t становить , а ціна одиниці продукції — , то послідовність цін { } збігається до рівноваги .

Справді, оскільки ціна у періоді t + 1 становить

, ,

то при

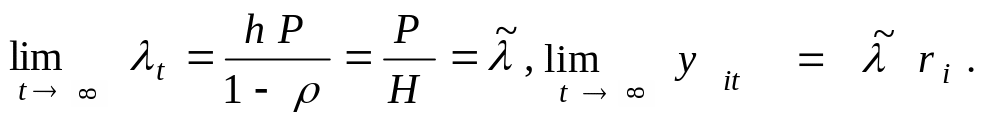
Отже, послідовність { } збігається до оптимальних обсягів випуску продукції { }, а послідовність цін { } — до ціни . При цьому гарантією збіжності є умова , де — максимально можливе значення всіх .

Складною є ситуація в разі врахування виконавцями впливу обсягу випуску продукції на її ціну, тобто за сильних штрафів з боку GB.

Згідно з [17] у цьому разі цільова функція і-того виконавця матиме вигляд

Нехай виконавець приймає ціну за рівноважну та відповідно визначає рівноважний випуск продукції . Пару параметрів { , } вважають рівноважною, якщо і послідовність { } забезпечує максимум цільової функції на множині послідовностей { }. Для таких послідовностей цільова функція матиме вигляд

, (2.38)

,

де називають «рівнем далекоглядності» і-того виконавця.

Прирівнюючи до нуля часткову похідну цільової функції (2.38) по , маємо

,

звідки .

Оскільки в умовах рівноваги випуск продукції становить , то , а тому 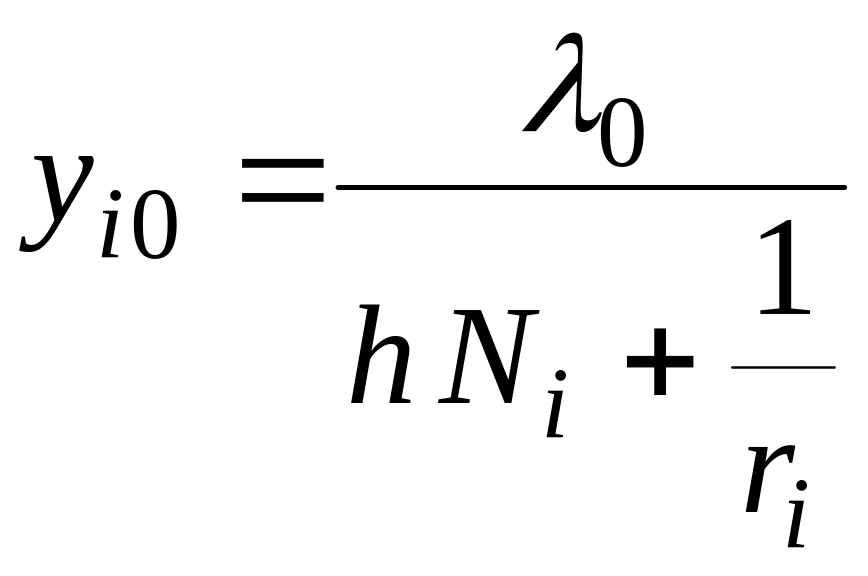, тобто обсяг випуску продукції у періоді t = 0 обчислюють за допомогою її ціни у цьому періоді.

Розглянемо послідовність обсягів випуску продукції в наступні періоди:

, .

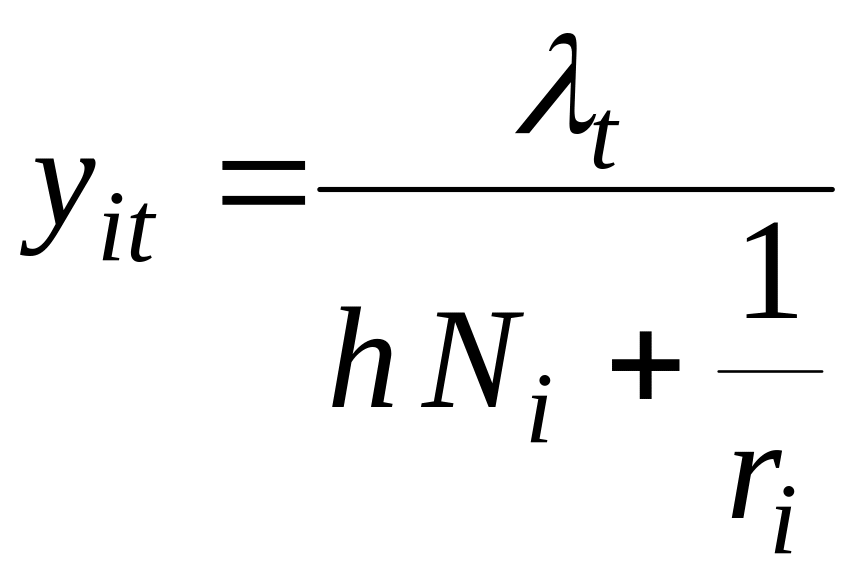Очевидно, що

, .

Введемо позначення , тоді .

Враховуючи [17], що при для будь-якого

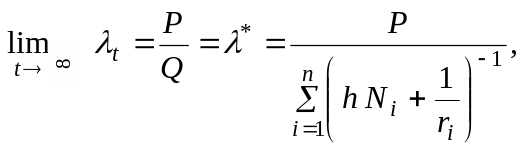
маємо

Оскільки — убуваюча функція від і зростаюча функція від , то , що й є умовою збіжності цін.

Аналіз ситуації рівноваги за припущення хоча б для одного виконавця свідчить, що , а обсяги випуску продукції { } можуть бути неоптимальними. Дійсно, якщо для всіх виконавців , то і не залежить від . Крім того, якщо більш ефективний виконавець є й більш далекоглядним ( ), то , тобто і знаходяться в обернено пропорційній залежності, а не у прямо пропорційній як в оптимальному плані.

Проаналізуємо ефект монопольного виконавця у цій ситуації. При ( ) та маємо

,

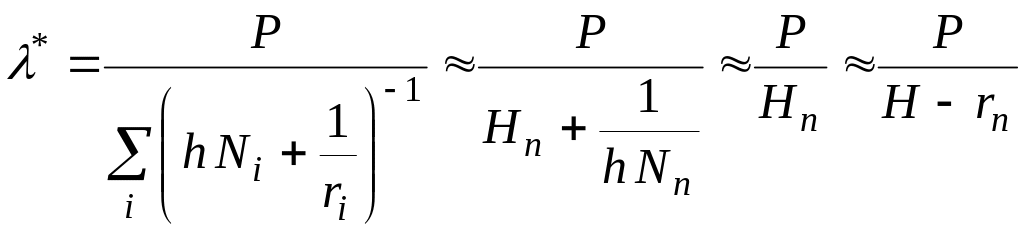звідки при .

Слід наголосити, що прояв монопольного ефекту у цьому разі тісно пов’язаний із далекоглядністю виконавця-монополіста. Дійсно, якщо для всіх виконавців, то не залежить від наявності монополіста в системі. Якщо ж для всіх виконавців, то ціна

також не залежитиме від наявності монополіста у системі.

У разі коли деякі виконавці є «дуже далекоглядними» , а інші — недалекоглядними ( , ), маємо

, , .

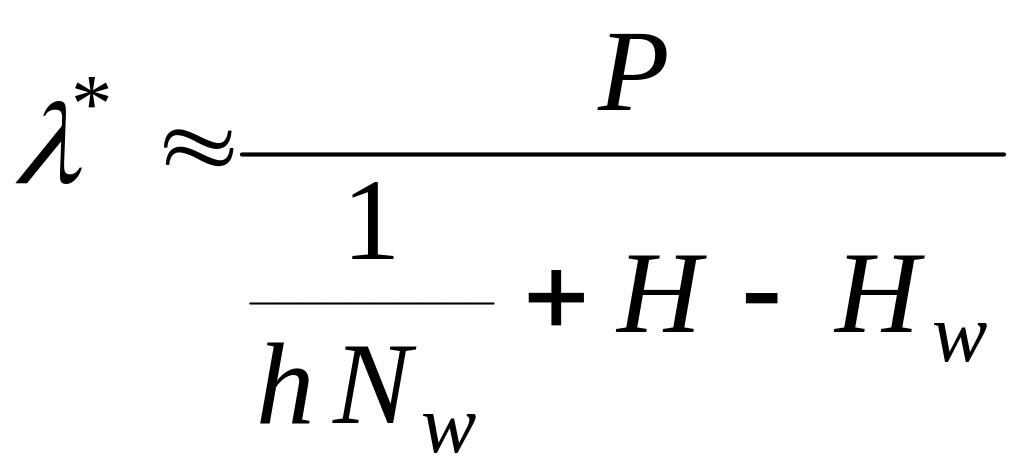Якщо при цьому то .

Згідно з викладеним за виконання умов , , ( ), що свідчать про наявність в організаційній системі «дуже далекоглядного» виконавця, маємо:

, , , .

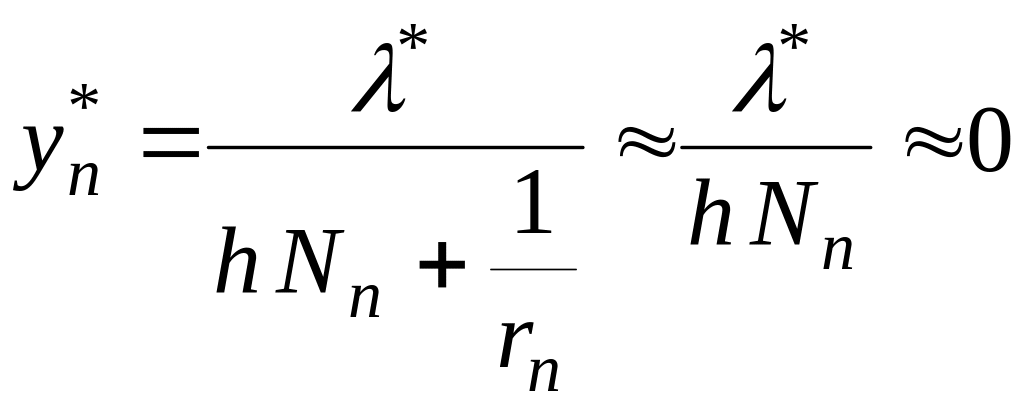Економічна інтерпретація цих формул вказує на виникнення парадоксальної ситуації в ОС з «дуже далекоглядним» виконавцем: останній фактично не випускає продукцію, і його прибуток дорівнює нулю, разом із тим він отримує у кожному періоді прибуток . Ця ситуація свідчить, що прогнозуючи розвиток виробництва, не слід втрачати керування процесом виконання поточного плану.

Крім розглянутого методу встановлення ціни на продукцію організаційної системи існують також інші, ґрунтовані на адаптивному способі формування даних [17]. Розглянемо один із них.

Припустимо, що виконавці функціонують у періоді t на підставі гіпотези слабкого впливу, тобто при GB може визначити

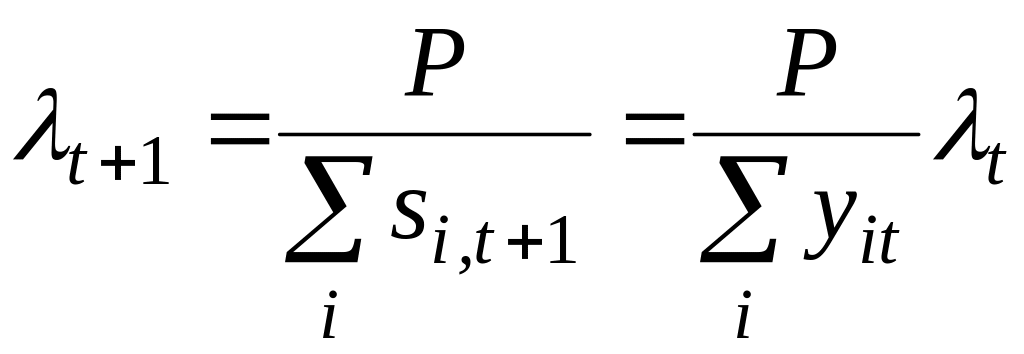. (2.39)

За таким способом визначення ціни забезпечується її збіжність у ситуацію рівноваги за один період незалежно від початкової ціни .

Проаналізуємо ситуацію рівноваги з урахуванням далекоглядності виконавців, припускаючи, що вони обирають , вважаючи ціну рівноважною.

Підставляючи (2.39) у цільову функцію (2.38) з урахуванням , маємо

.

Прирівняємо до нуля похідну від по ,

.

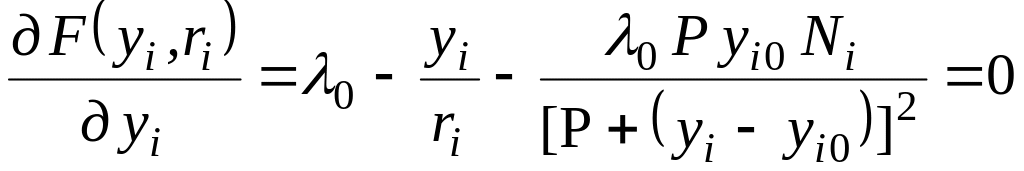Розв’язання цього рівняння з урахуванням умови дає змогу визначити обсяг випуску продукції і-того виконавця за ціною :

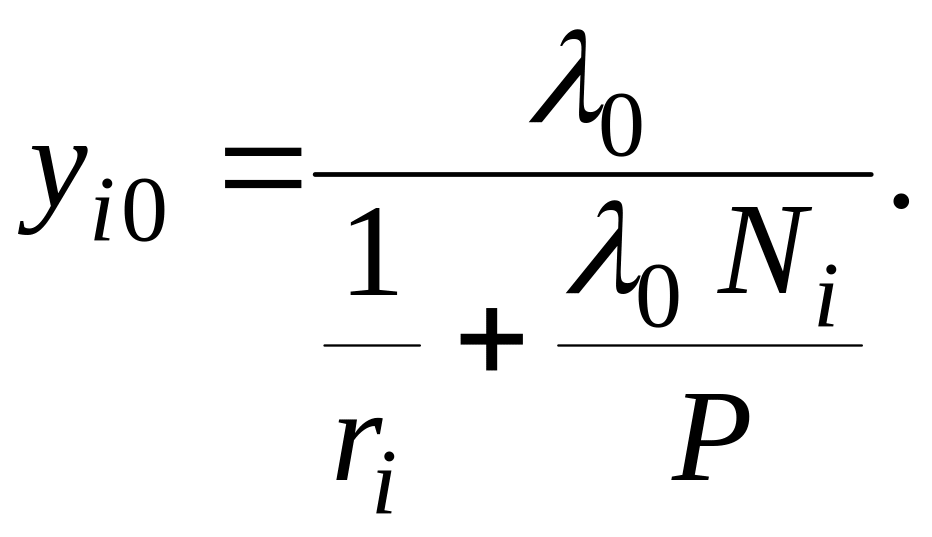
Отже, ціна визначається за формулою:

, ,

а рівноважна ціна — за формулою:

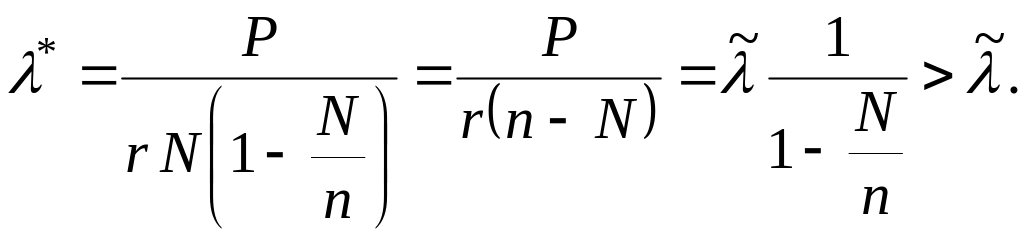
Послідовність { } збігається у цьому разі за умови , а у разі , тобто коли , — за умови n > N.

Повна централізація планування. Розглянемо довільну цільову функцію GB Ф і цільові функції виконавців .

Введемо позначення:

— множина пар , для яких і

; (2.40)

— множина таких, що ;

— множина таких, що ∅.

Порівняємо системи з різним рівнем централізації планування за критерієм максимізації функціонала Ф .

Для ринкової системи вважається, що в рівновазі встановлюється єдина ціна продукції, а обсяги випусків продукції виконавців забезпечують за цієї ціни максимум їхніх цільових функцій. Таким чином, є множиною ситуацій рівноваги та досягається гарантоване значення цільової функції GB:

. (2.41)

Для систем з повною децентралізацією планування також є множиною ситуацій рівноваги, але, оскільки GB встановлює ціну , то він може забезпечити гарантоване значення цільової функції:

. (2.42)

Для систем з частковою централізацією планування, коли випуск продукції планується і реалізація y збігається з планом x, а витрати не плануються, механізм відкритого керування (ВК), для якого умови рівноваги за гіпотези слабкого впливу мають вигляд (2.40) і який є оптимальним на множині [17], забезпечує значення функціоналу:

. (2.43)

З порівняння (2.43) з (2.42) і (2.41) випливає, що механізм відкритого керування забезпечує вищу ефективність функціонування системи, ніж будь-який механізм ціноутворення в системах з повною децентралізацією планування, у тому числі і (2.39), і в ринковій системі.

Цілком природно, що якщо для будь-якого механізму ціноутворення ситуацією рівноваги за гіпотези слабкого впливу є , то зі збільшенням рівня централізації буде залишатися ситуацією рівноваги.

Отже, оптимальний механізм функціонування системи існує на множині механізмів з повною централізацією планування. Однак у практиці керування такі системи можуть виявитися неприйнятними з деяких міркувань (обмеження на розмір штрафів, кількість планових показників тощо). Тому виникають складні задачі визначення оптимальних механізмів на множині систем з частковою централізацією планування. Крім того, слід ураховувати той факт, що висновок про ефективність системи з повною централізацією планування зроблено за умови, якщо витрати на керування (збирання і формування потрібних даних, вирішення відповідних задач прийняття управлінських рішень, здійснення контролю, застосування економічних санкцій тощо) не враховуються. У ринкових системах планування витрати на керування мінімальні, у системах з повною централізацією планування — максимальні. З урахуванням витрат на керування оптимальним механізмом функціонування системи може бути деякий частково централізований механізм.