2.4. Механізми внутрішньосистемного ціноутворення

Потреба у визначенні внутрішньосистемних цін виникає у разі, коли після укладення керівним органом угоди з зовнішнім замовником на випуск продукції в обсязі P і вартістю С потрібно розподілити цей обсяг і майбутній прибуток між підрозділами (виконавцями) системи.

У ході розроблення механізмів внутрішніх цін ОС (внутрішньосистемного ціноутворення) слід розглядати два випадки.

Перший із них трапляється під час виробництва однотипної продукції, коли кожен виконавець може виробляти цю продукцію, і задача полягає в розподілі її обсягу між ними, другий — коли кожен виконавець спеціалізується на виробництві певного виду продукції, причому ту, що може виробляти один виконавець, не може виробляти інший. У цьому разі задача полягає у визначенні договірних цін на виробництво продукції кожним виконавцем.

Розглянемо випадок розподілу однотипної продукції.

Позначивши через обсяг виробництва продукції і-тим виконавцем, а — його витрати на виконання цього обсягу, можна визначити прибуток і-того виконавця: , де ц — ринкова ціна одиниці продукції.

Відповідно прибуток системи загалом становитиме:

,

де n — загальна кількість виконавців ОС;

V — загальні витрати на випуск продукції в обсязі .

За припущення, що кожен виконавець матиме певний відсоток від отриманого ним прибутку, його цільова функція набуває вигляд:

.

Визначимо залежність витрат виконавця від обсягу виробництва продукції.

Управлінський облік [108] розподіляє витрати на випуск продукції на умовно-змінні та умовно-постійні. Взаємозв'язок витрат, доходу і прибутку дає змогу формалізувати залежність витрат від обсягу випуску або реалізації продукції.

Ця залежність має такий аналітичний вигляд:

,

де — умовно-постійні витрати;

— умовно-змінні витрати.

Графічне зображення цієї функції наведено на рис. 2.4.

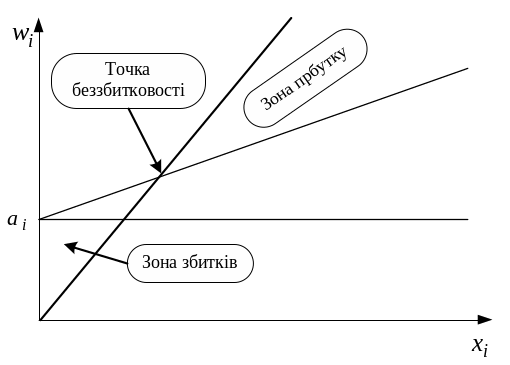
Рис. 2.4. Залежність витрат від обсягу реалізації продукції

У такому разі собівартість випуску одиниці продукції обчислюють за формулою

,

а її графічне зображення подано на рис. 2.5.

Рис. 2.5. Гіперболічна форма зміни собівартості випуску одиниці продукції

Якщо наявні виробничі потужності обмежені, ця гіперболічна залежність змінюється на параболічну (рис. 2.6).

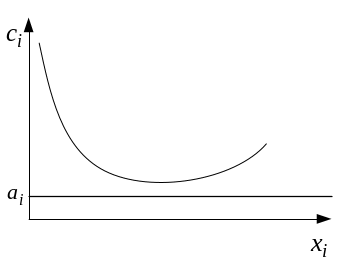
Рис. 2.6. Параболічна форма зміни собівартості випуску одиниці продукції

У цьому разі змінюється і форма залежності витрат від обсягу випуску продукції (рис. 2.7), яку відображають рівнянням параболи:

,

де — коефіцієнт, що характеризує ефективність роботи і-того виконавця.

Рис. 2.7. Параболічна залежність витрат від обсягу реалізації продукції

З урахуванням викладеного прибуток системи становитиме

. (2.15)

Для досягнення системою найбільшого прибутку потрібно так розподілити загальний обсяг випуску продукції P, щоб функція цілі (2.15) набувала максимального значення, тобто реалізувати оптимізаційну модель

, (2.16)

. (2.17)

Задача (2.16) — (2.17) належить до класу задач на умовний екстремум, яка може бути вирішена за допомогою методу множників Лагранжа.

Функція Лагранжа для цієї задачі має вигляд:

,

де — множник Лагранжа.

Для визначення точки максимуму функції Лагранжа знайдемо часткові похідні від неї по невідомих змінних і прирівняємо їх до нуля:

(2.18)

Розв’язком першого рівняння системи (2.18) є

. (2.19)

Після підстановки (2.19) у друге рівняння системи (2.18) маємо

,

звідки визначають множник Лагранжа

.

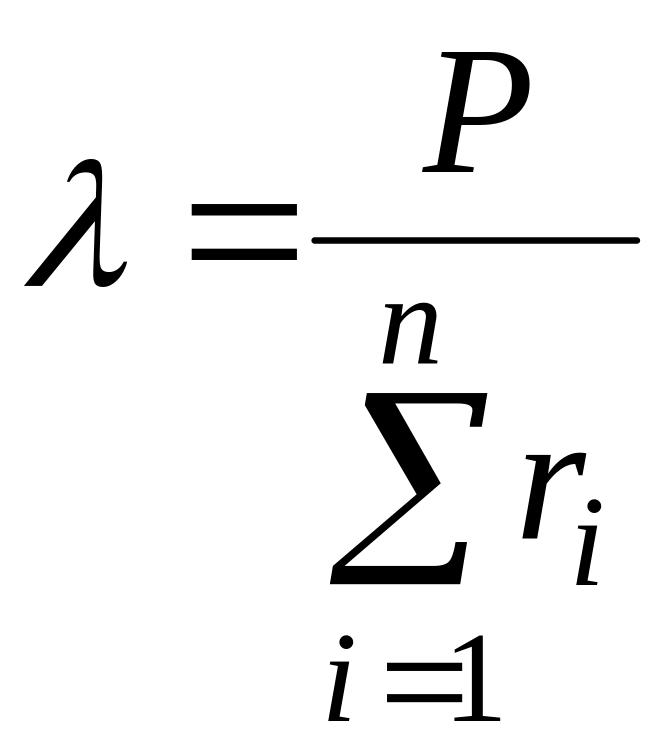Підставляючи значення множника Лагранжа в (2.19), одержимо

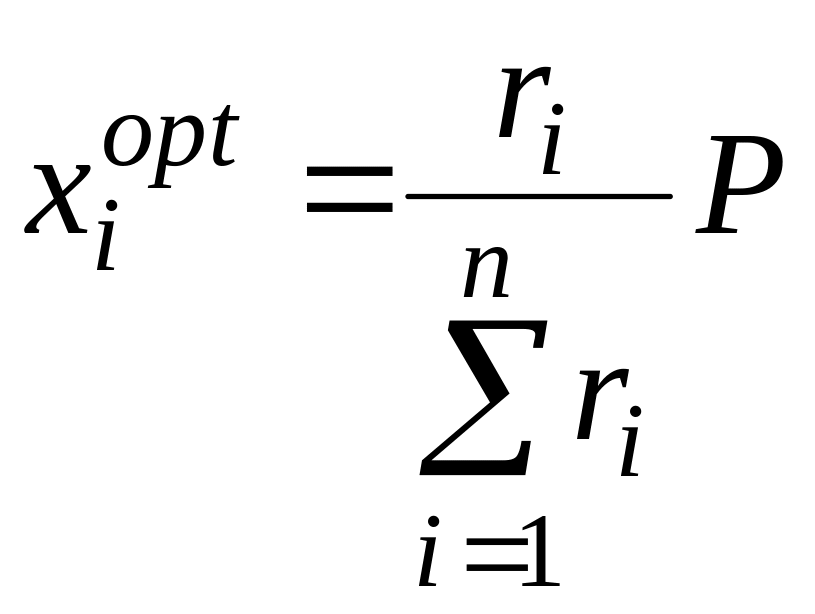. (2.20)

Таким чином, оптимальний план розподілу замовлення з погляду керівного органу для i-того виконавця прямо пропорційний обсягу випуску продукції P і відношенню ефективності i-того виконавця до суми ефективностей усіх виконавців.

Із (2.16) і (2.20) визначають максимальне значення цільової функції (максимально можливий прибуток організаційної системи).

Очевидно, кожен виконавець зацікавлений у максимізації свого прибутку, тобто тієї частини системного прибутку, що залишається у його розпорядженні:

,

де — розподіл випуску продукції з погляду і-того виконавця.

Із рівняння знаходять оптимальний з погляду і-того виконавця обсяг випуску продукції . Але зазвичай у процесі розподілу випуску продукції GB керується заявками виконавців ( ). Якщо виявиться, що , то кожен виконавець отримає обсяг випуску продукції . Якщо ця рівність не виконується, то здійснюють розподіл величини Р пропорційно заявкам виконавців за формулою

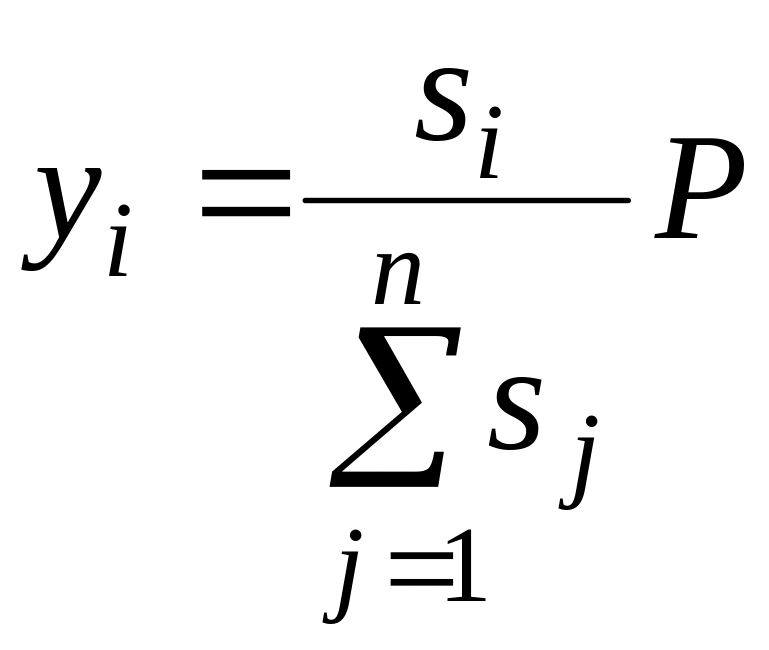. (2.21)

Отже, отримання виконавцем максимального прибутку відповідає тому, що його заявка становить , а обсяг випуску продукції визначають за (2.20). При цьому система отримує максимальний прибуток. Але виконавці зацікавлені у збільшенні свого прибутку. Залежно від заявок і розподілу Р згідно з (2.21) прибуток і-того виконавця визначають за формулою

,

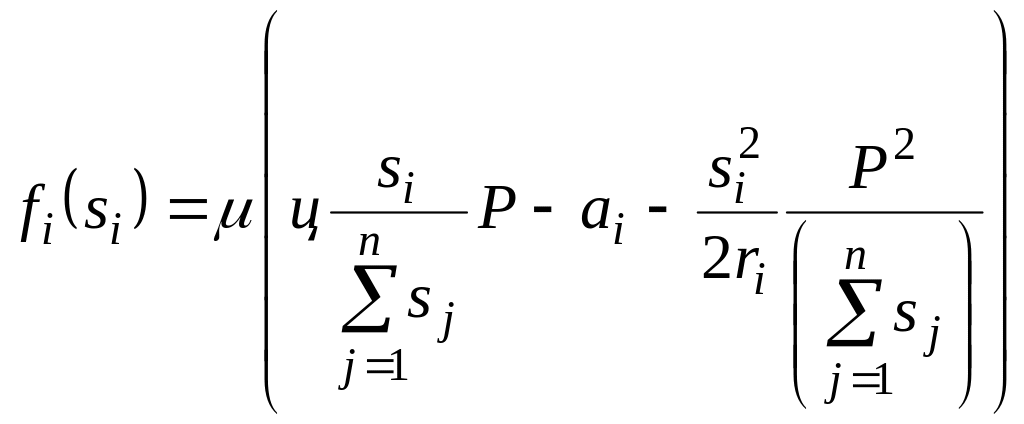а його максимум — з умови

.

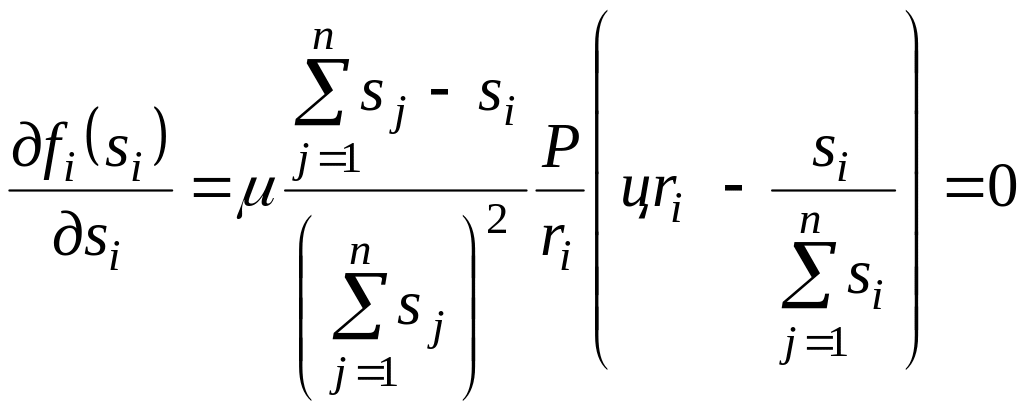Оскільки , тоді, якщо виконується умова ( ), то всі виконавці будуть подавати заявки , якщо не виконується — . Така ситуація є гарантованою і рівноважною. При цьому всі виконавці отримають однакові випуски продукції. Але слід наголосити, що такий розподіл загального випуску продукції не є оптимальним за винятком ситуації, коли . Отже, розглянутий механізм розподілу Р не завжди ефективний.

Порівняння (2.20) з виразом свідчить про наявність конфлікту між інтересами GB та виконавців, оскільки виконавцям вигідно виробляти продукцію в обсязі, що перевищує Р:

.

У цій ситуації виконавці, бажаючи отримати у сумі більший обсяг випуску, ніж у наявності, будуть надавати недостовірну інформацію. Тому виникає завдання створення такої системи керування, яка узгоджувала б інтереси GB і виконавців. Цього можна домогтися шляхом зменшення ринкової ціни ц до рівня, за яким сума оптимальних планів для виконавців була б рівною наявному Р. GB не може вплинути на ринкову ціну ц, але може ввести внутрішню ціну для взаєморозрахунків із виконавцями. Отже, крім визначення плану розподілу обсягу випуску продукції слід визначити внутрішню ціну , ураховуючи, що виконавці вибирають дії виходячи з максимізації своїх цільових функцій.

Вирішення цієї задачі здійснюють способом реалізації моделі:

(2.22)

(2.23)

(2.24)

Прирівнюючи до нуля диференціал функції (2.24), визначають оптимальний план i-того виконавця як функцію внутрішньої ціни:

. (2.25)

Підставляючи (2.25) у (2.23), визначають внутрішню ціну:

. (2.26)

Реалізація моделі (2.22) — (2.24) за допомогою методу множників Лагранжа дає змогу визначити

(2.27)

та оптимальний план

. (2.28)

Із (2.26) і (2.27) випливає, що множник Лагранжа становить внутрішню ціну організаційної системи .

Оскільки параметри GB невідомі, замінимо їх у (2.27) і (2.28) на відомі оцінки : , .

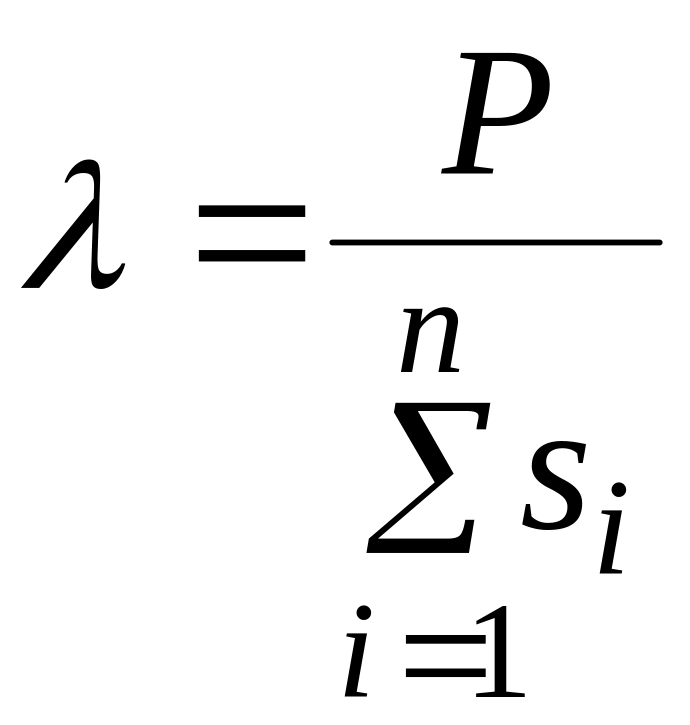Підставимо та у цільову функцію виконавця:

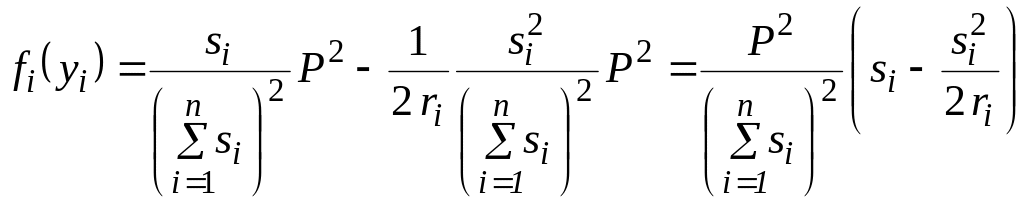, . (2.29)

Функція залежить лише від повідомлень виконавців. Для перевірки їхньої неманіпульованості припустимо, що кожен виконавець своїм повідомленням не впливає на загальний для всіх виконавців керований параметр — внутрішню ціну (гіпотеза слабкого впливу для ОС з великою кількістю виконавців). При цьому знаменник цільової функції не залежатиме від повідомлення і-того виконавця, тобто його можна вважати константою.

Прирівнявши результат диференціювання (2.29) до нуля, отримаємо:

, ,

звідки випливає, що повідомлення достовірної інформації вигідно всім виконавцям, а отже, механізм внутрішніх цін є неманіпульованим.

На підставі внутрішньої ціни можна ввести поняття внутрішнього прибутку як фіктивного прибутку, обчисленого за формулою

, .

Відповідно формула для визначення фактичного прибутку F матиме вигляд:

.

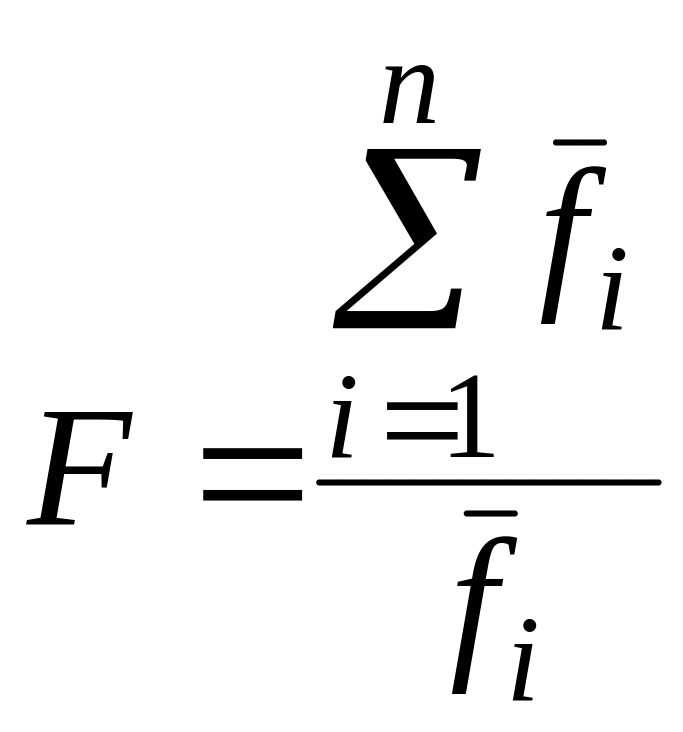У разі повідомлення достовірної інформації, тобто коли , , розподіл ресурсу буде оптимальним, а прибуток ОС — максимальним. Таким чином, механізм внутрішніх цін вельми унікальний: він є механізмом відкритого керування (відсутня маніпуляція), що має ту саму ефективність, що й механізм в умовах повної інформованості, та мінімізує сумарні витрати виконавців на виконання загального планового завдання. Крім того, за цим механізмом узгодженими є інтереси GB і виконавців, а GB отримує максимально можливий прибуток.

Розглянемо другий випадок визначення внутрішніх цін, коли організаційна система згідно з угодою має виробляти продукцію широкої номенклатури, а кожен виконавець — тільки один її вид. У цьому разі ситуація змінюється: відпадає потреба в розподілі обсягів виробництва продукції, натомість постає задача визначення обсягів фінансового забезпечення виробничого процесу кожного виконавця.

Одним з варіантів рішення цієї задачі є використання принципу рівних рентабельностей [69]. Визначатимемо рентабельність як прибуток на одиницю витрат. Тоді рентабельність на рівні системи становить , а на рівні і-того виконавця — , де — вартість продукції.

За принципом рівних рентабельностей

, (2.30)

. (2.31)

Із рівняння (2.30) отримуємо: або , звідки . Остаточно матимемо .

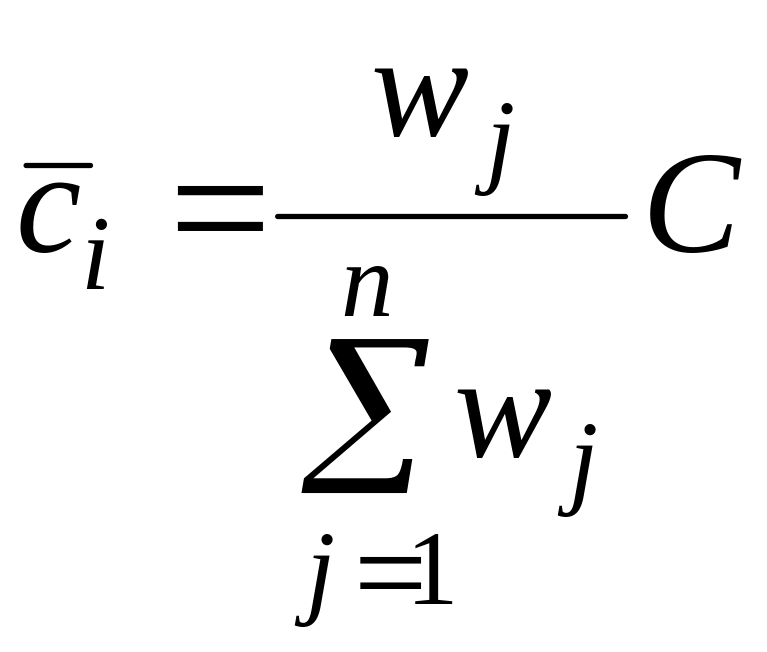Оскільки GB за наявності маніпулювання інформацією з боку виконавців з метою збільшення прибутку не володіє точними значеннями витрат , він використовує для визначення обсягів фінансування оцінки ( ) цих витрат, отримані від кожного з виконавців. Тоді 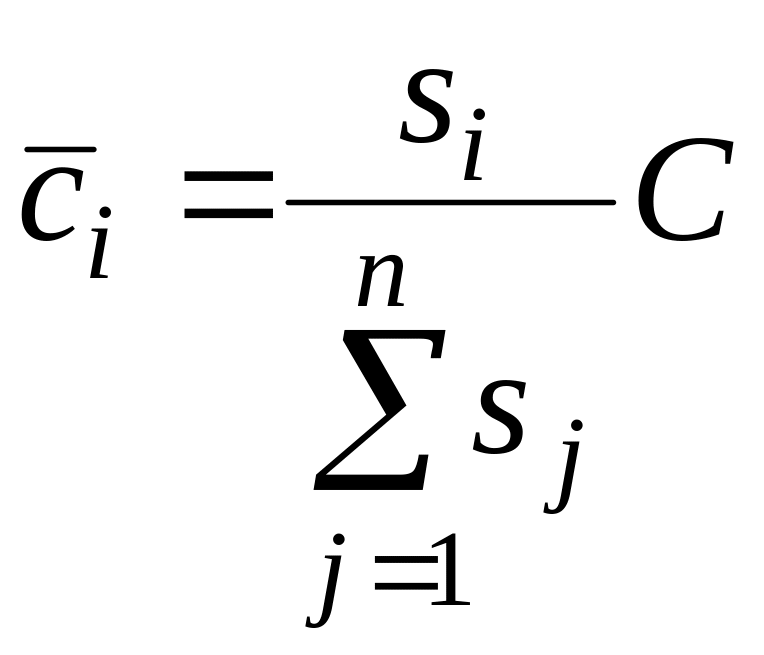, а формула для визначення прибутку і-того виконавця має вигляд

.

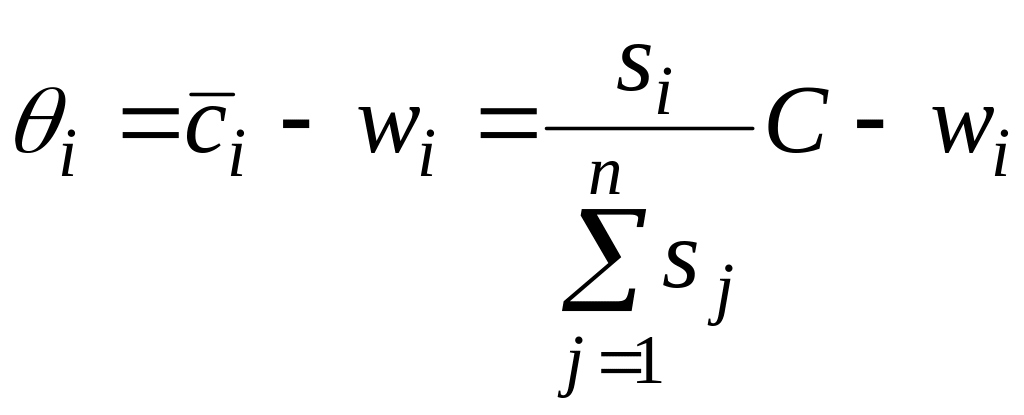Для усунення маніпулювання інформацією з боку виконавців введемо додаткові відрахування від надпланового прибутку. Тоді (2.31) набуває вигляду

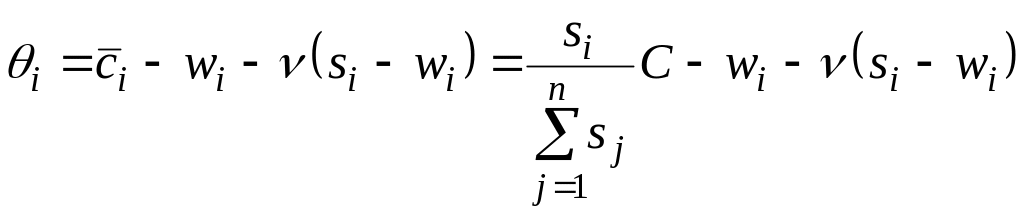, (2.32)

де — коефіцієнт додаткових відрахувань від надпланового прибутку.

Із системи рівнянь знаходимо 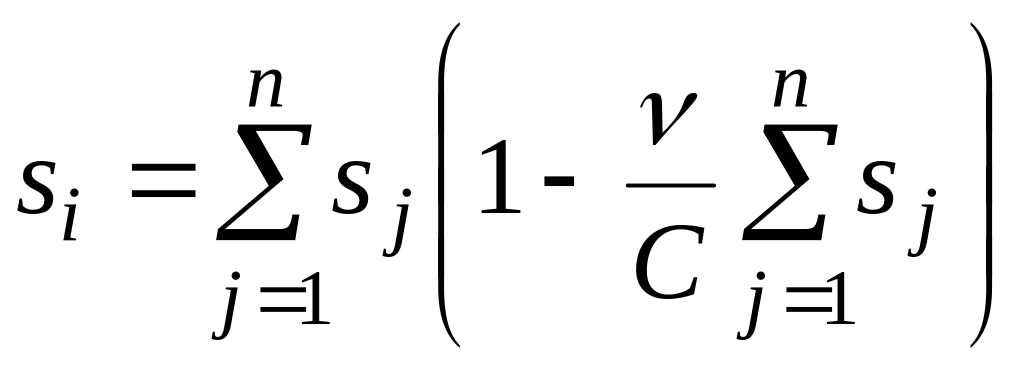, звідки маємо за умови ситуацію рівноваги за Нешем:

.

Цілком зрозуміло, що виконавцю не вигідно сповіщати GB завищену заявку, якщо при цьому буде знижуватися його прибуток, тобто якщо

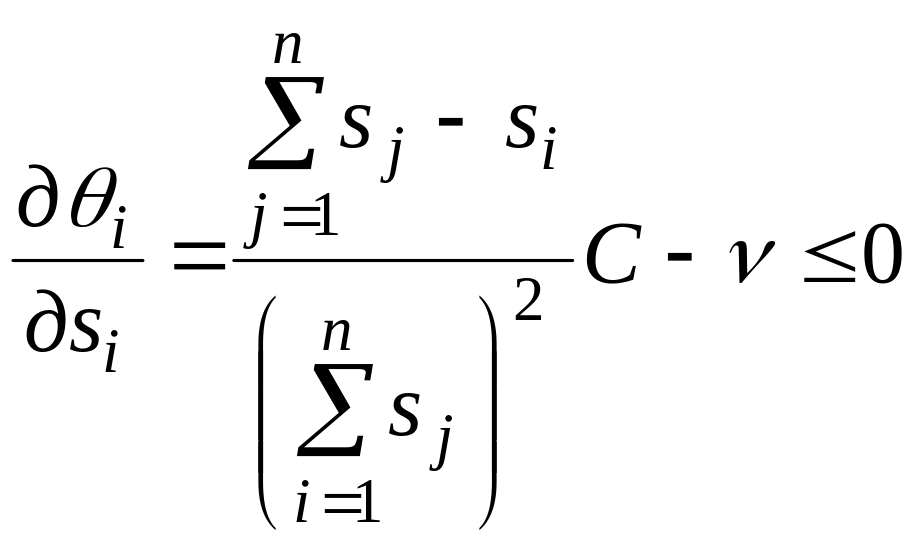або .

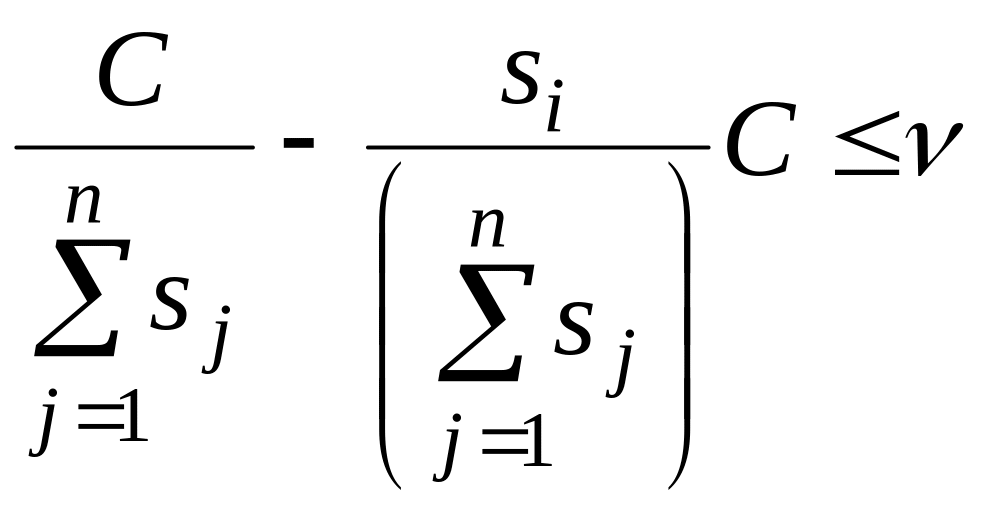Віднявши одиницю від обох частин цієї нерівності, перетворимо її до вигляду

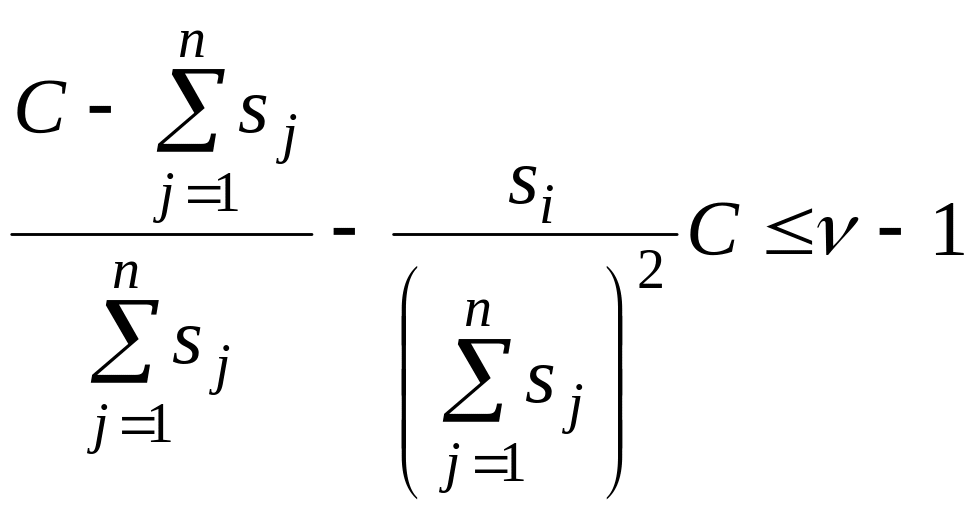. (2.33)

З урахуванням рентабельності, що визначається на передплановій стадії, формула (2.33) набуває вигляду

.

Віднімаючи одиницю від обох частин цієї нерівності, її перетворюють до вигляду:

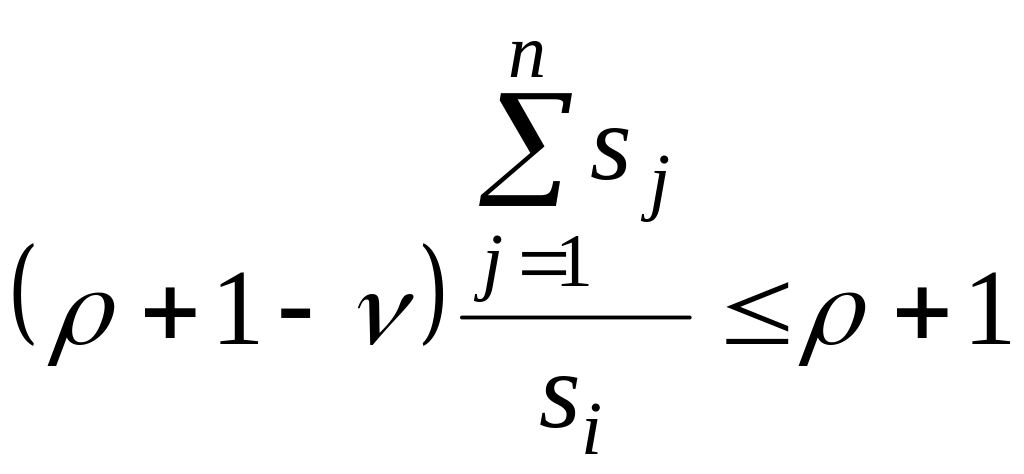, або .

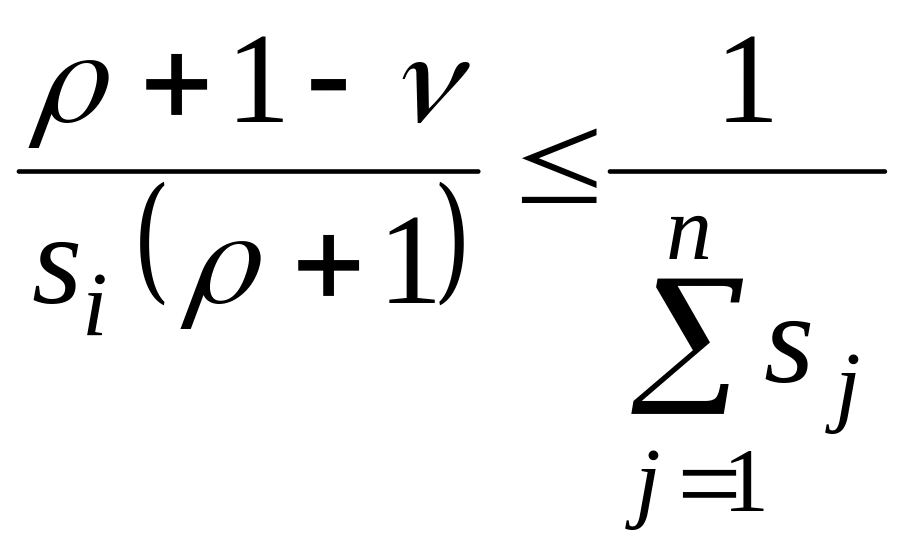Після простих перетворень (множення обох частин на С і віднімання від них по 1) остання нерівність набуває вигляду

. (2.34)

Якщо GB залишає виконавців без прибутку ( ), то при нерівність (2.34) буде виконуватися за умови , з урахуванням якої у разі (2.34) набуває вигляду

, або .

Помноживши цю нерівність на та враховуючи, що , маємо

(2.35)

або

.

Таким чином, тільки для низькорентабельних угод можна сподіватися, що принцип рівних рентабельностей забезпечить достовірність оцінок витрат, які повідомляють виконавці системи.

У разі коли GB не тільки позбавляє виконавців надпланового прибутку, а й штрафує їх за завищення оцінок витрат, тобто коли , нерівність (2.34) має вигляд

,

де — коефіцієнт штрафу за завищення витрат.

Якщо до того ж виконавці є однаковими з позицій рентабельності, то (2.35) набуває вигляду:

, або ,

звідки випливає, що обмеження на максимальну рентабельність стає менш жорстким.

З прикладами практичного використання механізмів ціноутворення можна ознайомитися за джерелами [79; 88; 119].