2.3. Механізми перерозподілу ресурсів

Чимала кількість економічних задач може бути сформульована як задача обміну, що розуміють як процес перерозподілу ресурсів між учасниками організаційної системи [54; 91]. Розглянемо можливість застосування методу побудови механізмів обміну для вирішення задач планування у керуванні організаційною системою. В основу методу покладено сформульований у параграфі 2.2 принцип відкритого керування. Його використання дає змогу отримувати ефективні рішення для задач обміну за неповної інформованості GB щодо параметрів виконавців.

Схему, за якою учасники організаційної системи зацікавлені у взаємодії між собою, тобто у перерозподілі ресурсів, називають обмінною.

Учасниками в задачі планування цін за обмінною схемою є виробник товару, який виступає в ролі GB, і покупець, який виступає в ролі виконавця. Ресурсами в задачі ціноутворення є довільно подільний товар і гроші.

Задача полягає в здійсненні найвигіднішого для GB обміну з виконавцем, тобто розподілу ресурсу. GB не має точної інформації про параметр, від якого залежить функція корисності діяльності виконавця (ефективність його діяльності, продуктивність праці тощо) та який називають типом виконавця. GB пропонує виконавцю такий механізм обміну: залежно від повідомленої виконавцем оцінки свого типу йому призначають різні варіанти обміну.

Зазвичай вводять такий тип, щоб відображати «корисність» діяльності виконавця для GB: чим «кращий» тип виконавця (більше його абсолютне значення), тим більший прибуток може отримати GB від взаємодії з виконавцем. У задачі планування це означає, що чим вищий тип виконавця, тим вище він оцінює пропонований йому товар.

Побудова неманіпульованих механізмів обміну ґрунтована на принципі досконалого узгодження (див. п. 2.2). Варіант обміну, що відповідає заявці виконавця, має бути найвигіднішим з усіх пропонованих варіантів обміну для виконавця, чий тип відповідає даній заявці. Тим самим GB спонукає виконавця повідомляти реальне значення свого типу.

Загальна модель перерозподілу ресурсів. Розглянемо організаційну систему, що складається з GB, (n + 1)-го CE і m видів ресурсів. Виконавці можуть взаємодіяти між собою через взаємний обмін ресурсами. Множину всіх виконавців позначимо I = {0,1,2,...,n}, а множину всіх ресурсів — J = {1,2,...,m}. Набір наявних у і-того виконавця ресурсів позначимо , де — обсяг наявних у і-того виконавця ресурсів j-того типу. Відповідно розподіл ресурсів між усіма виконавцями має вигляд матриці: . Обмін розглядають як перерозподіл ресурсів з множини J між елементами з множини I: → , де — матриця початкового або поточного розподілу ресурсу, — кінцевого розподілу відповідно.

Нумерація виконавців від 0 до n виправдана тим, що організаційну систему розглядають як активну, тобто таку, що складається з одного керівного виконавця і n підлеглих йому виконавців, що мають можливість взаємодіяти між собою завдяки взаємному обміну ресурсами.

Модель активної системи (АС) задають набором таких параметрів:

склад АС — сукупність суб'єктів, які є учасниками системи;

структура АС — сукупність інформаційних, керівних та інших зв'язків між учасниками АС включно з відносинами підпорядкованості та розподілу прав прийняття рішень;

порядок функціонування — послідовність отримання інформації та вибору дій (планів, що задає GB) учасниками АС;

кількість періодів функціонування — відображає наявність або відсутність динаміки в АС;

уподобання учасників АС — визначають спільно з принципами раціональної поведінки залежність стану системи від керівних впливів і критерій ефективності системи;

допустимі множини станів учасників АС — відображають індивідуальні та загальні обмеження на вибір станів, зумовлені навколишнім середовищем, використовуваною технологією тощо;

інформованість учасників — інформація, якою володіють учасники.

Опишемо модель організаційної системи, що реалізує задачу розподілу ресурсів [10; 39; 40; 45; 79] у термінах обмінних схем.

Нехай функції переваги учасників організаційної системи мають вигляд:

, .

Як і будь-яка математична модель, модель обміну має охоплювати певні обмеження, що накладають на її змінні величини. До них належать:

обмеження з ресурсів;

обмеження з можливості взаємодії між виконавцями;

обмеження на вид функцій переваги виконавців;

обмеження індивідуальної раціональності.

Розглянемо сутність цих обмежень і наведемо конкретні приклади.

Обмеження з ресурсів визначають множини значень матриці розподілу ресурсів. Прикладом є обмеження на загальну кількість ресурсу і на кількість ресурсу в окремого виконавця, приміром .

Обмеження з можливості взаємодії між виконавцями перетворюють деякий довільний набір виконавців на мережеву структуру, вказуючи, з якими виконавцями конкретний виконавець може обмінюватися та якими ресурсами.

На рис. 2.3 наведено приклад обмежень цього класу, лінії на якому вказують на можливість взаємодії (обміну) між виконавцями, підписи до ліній — на типи ресурсів, якими вони можуть обмінюватися. Обмеження цього типу позначимо . Запис → означає, що обмін → можливий у межах певної структури.

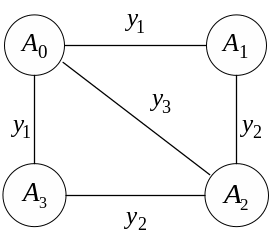
Рис. 2.3. Структура взаємодії виконавців

Обмеження на вид функцій переваги виконавців належать до урізноманітненого класу обмежень. Функції всіх виконавців належать до класу ввігнутих однопікових неперервних функцій і задають їх в явному вигляді. Їхній максимум досягається за наявності у і-того виконавця ресурсу в обсязі . Обмеження цього класу позначають .

Обмеження індивідуальної раціональності визначають вимоги, що накладають на значення функцій переваги виконавців, наприклад:

.

Множину розподілів ресурсів, що індивідуально раціональні до їхнього початкового розподілу, позначають . Очевидно, .

Використовуючи обмеження наведених чотирьох класів у різних комбінаціях, можна отримати чималу кількість моделей взаємодії виконавців.

Виходячи із сутності розглянутих обмежень можна сформулювати такі ключові визначення:

множина можливих варіантів обміну (МВО) — це сукупність усіх індивідуально раціональних розподілів ресурсів, перехід до яких від початкового розподілу ресурсів можливий у межах заданої структури, тобто

;

обмінна схема — це кортеж , для якого МВО не пуста;

трансферт j-того ресурсу для і-того виконавця у процесі обміну — ;

вектор трансфертів усіх ресурсів і-того виконавця — ;

матриця трансфертів — ;

множина можливих варіантів обміну в термінах трансфертів:

;

функція корисності i-того виконавця від обміну — .

Властивості функції корисності ідентичні властивостям функції переваги. Функції корисності від обміну — це і є функції переваги, але такі, що мають нову систему координат (трансферти), отриману шляхом зрушення зі стартової системи координат (ресурси).

Загальна постановка задачі обміну може бути сформульована як стандартна задача керування [72; 79]. Реалізація будь-якого з варіантів обміну залежить від керівного впливу . Нехай на множині U × X заданий функціонал Ф (u, x), що визначає ефективність обміну з погляду керівного органу. Величину називають ефективністю керування . Задача керівного органу полягає у виборі максимально ефективного допустимого керування:

.

Із розглянутої моделі випливає, що задачі розподілу ресурсів (п. 2.2), а також задачі визначення внутрішніх цін організаційної системи (п. 2.4), в яких ресурсами для обміну є гроші і товари, можна розглядати як окремий випадок задач обміну (перерозподілу ресурсів).

Механізм відкритого керування перерозподілом ресурсів. Розглянемо систему, що складається із GB і n активних виконавців. Інтереси виконавців і GB виражають відповідно їхніми цільовими функціями:

та ,

де — параметр, що визначає клас допустимих цільових функцій i-того виконавця;

— вектор планів (дій), що призначає виконавцям GB,

— вектор дій, що обирають виконавці.

Функціонування системи здійснюють за такими етапами:

1) збирання інформації: виконавці повідомляють GB оцінки параметрів ;

2) планування: на підставі отриманих оцінок GB, використовуючи процедуру планування — де — множина допустимих планів, призначає виконавцям плани , ;

3) вибір стану: отримавши планові завдання, виконавці визначають свої стани, максимізуючи відповідні цільові функції:

,

де — множина допустимих станів і-того виконавця, .

У процесі повідомлення виконавцями оцінок може, як і за розглянутими вище механізмами, мати місце маніпулювання інформацією. Тому задача GB полягає у формуванні такої процедури планування, за якої досягає максимуму ефективність механізму перерозподілу ресурсів у точці рівноваги:

.

За отриманими і виконавці оптимізують свої дії за критеріями:

,

тобто функції уподобання (переваги) для них мають такий вигляд:

.

Отже, процедура планування здійснюватиметься за умовами:

(2.4)

(2.5)

За умовою (2.4) максимізують цільову функцію GB, а умова (2.5), що називають умовою досконалого узгодження [79], забезпечує призначення виконавцю плану, що максимізує його функцію уподобання, в яку підставляють повідомлену ним оцінку. Варіант обміну (перерозподілу), що відповідає заявці виконавця, має бути найвигіднішим з усіх пропонованих варіантів обміну для виконавця, чий тип відповідає даній заявці. Тим самим GB спонукає виконавця повідомляти справжнє значення свого типу.

Механізм, що задовольняє умовам (2.4) — (2.5), називають механізмом відкритого керування перерозподілом ресурсів. Він ґрунтований на принципі відкритого керування, за яким необхідною і достатньою умовою повідомлення виконавцем достовірної інформації при будь-яких є існування множин , для яких виконана умова досконалого узгодження [17; 54].

Оптимізація перерозподілу ресурсів за неповної інформації. Розглянемо схему перерозподілу ресурсів у системі, що складається з GB, n активних виконавців i m ресурсів. Нехай задані функції корисності виконавців, що залежать від вектора трансфертів ресурсів , . Параметр — тип виконавця, що характеризує його функцію корисності.

Виконавці інформовані асиметрично — GB знає всі параметри схеми, крім значень їхніх типів. Йому відомі лише множини можливих значень і, бути може, ймовірнісний розподіл типів на множині можливих значень. Тип активного виконавця відображає його цінність з погляду GB, а саме: чим вище тип, тим більшу користь GB може отримати від взаємодії з таким виконавцем.

Задача полягає у побудові механізму обміну , за яким

,

де — вектор заявок виконавців, за якими вони повідомляють GB оцінки своїх типів.

Таким чином, задача полягає у побудові прямого неманіпульованого механізму, тобто такого, для якого домінантною стратегією кожного виконавця буде повідомлення істинної заявки . Функціонування цього механізму має здійснюватися за розглянутою вище стандартною процедурою механізмів планування:

GB призначає механізм обміну ;

виконавці повідомляють GB свої заявки ;

GB призначає обмін .

Оскільки розглядається задача оптимізації перерозподілу ресурсів, то слід ввести потрібні для її вирішення обмеження (умови):

неперервність функції корисності;

існування її неперервних часткових похідних до другого порядку включно по всіх змінних;

монотонність часткових похідних функції корисності ;

сталість знака змішаної похідної 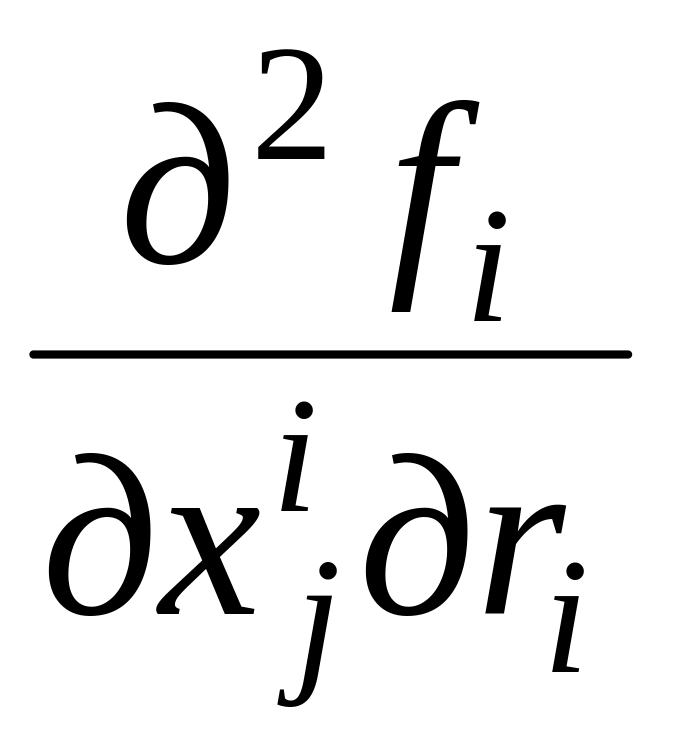(умова Спенса-Мірліса [54]), тобто :

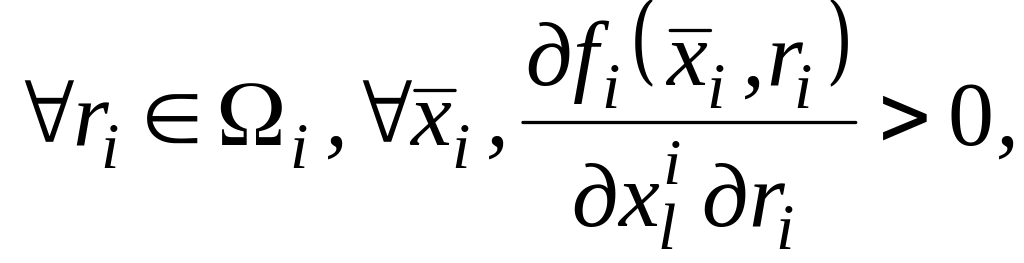та ;

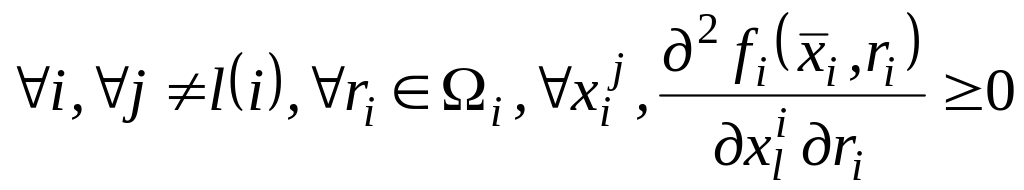забезпечення індивідуальної раціональності виконавців,

прибуток кожного виконавця не має бути негативним;

обсяг ресурсів обмежений;

можливість взаємодії виконавців за цією схемою обміну;

множина МВО не пуста;

прямий неманіпульований механізм має відповідати умові досконалого узгодження.

Введемо функцію залежності прибутку i-того виконавця від значення власного параметра заявки і заявки інших учасників обмінної схеми :

.

Тоді умову досконалого узгодження можна інтерпретувати таким чином:

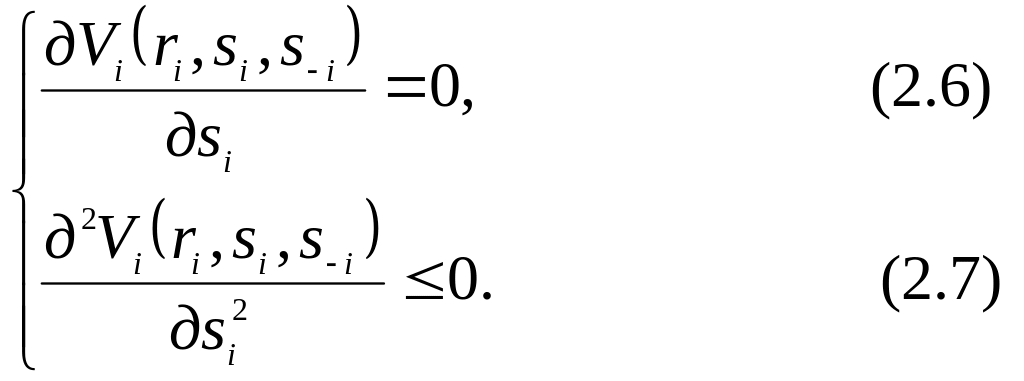
Згідно з [54] із (2.6) випливає, що:

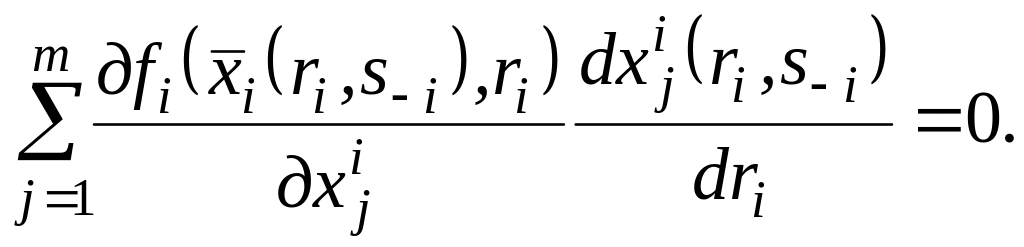(2.8)

Розглянемо умову (2.7) у розгорнутому вигляді:

+ .

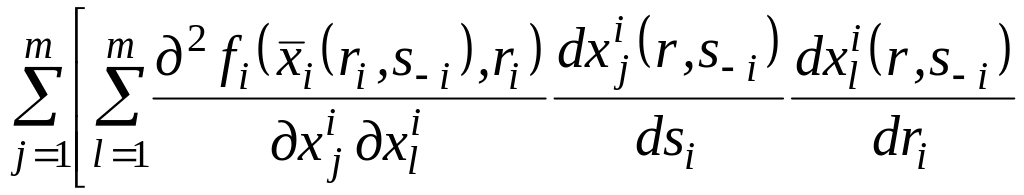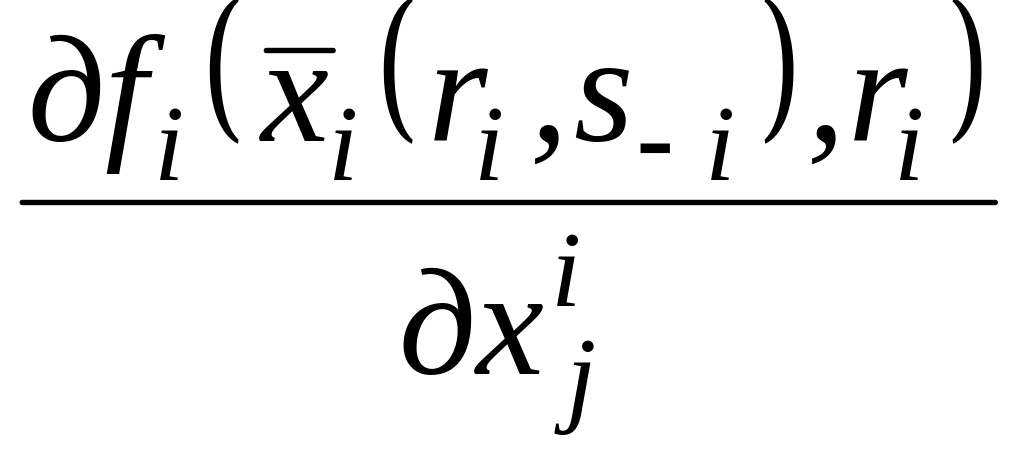
Продиференцюємо (2.8) по :

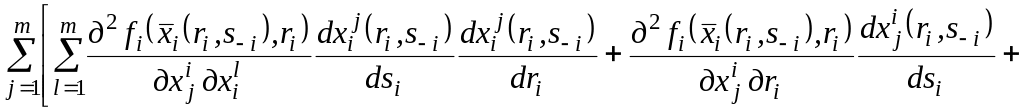
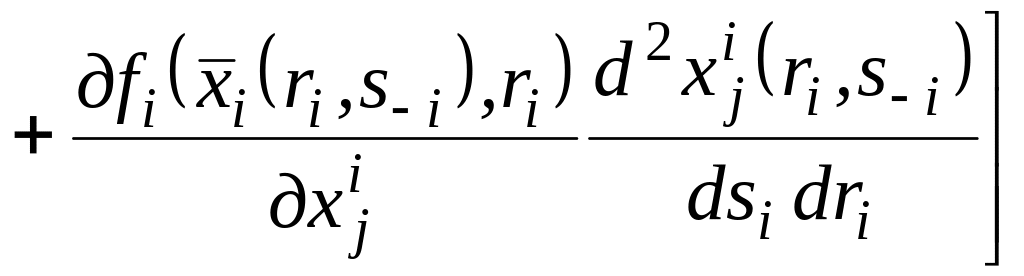=0. (2.9)

Враховуючи, що , і віднімаючи від рівності (2.9) умову (2.7) у розгорнутому вигляді, отримаємо:

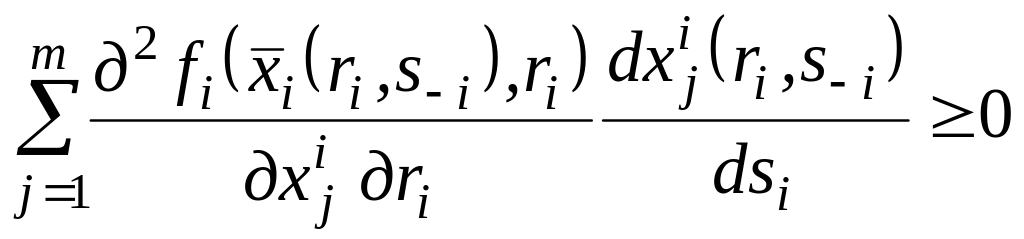, (2.10)

звідки можна зробити висновок, що умова (2.7) еквівалентна нерівності (2.10).

Доведемо, що за виконання умов (2.8) і (2.10) і монотонності всіх компонентів планів, призначених GB кожному з виконавців, тобто при виконанні умов

(2.11)

глобальний максимум цільової функції і-того виконавця досягається у разі, якщо .

Розглянемо вираз:

.

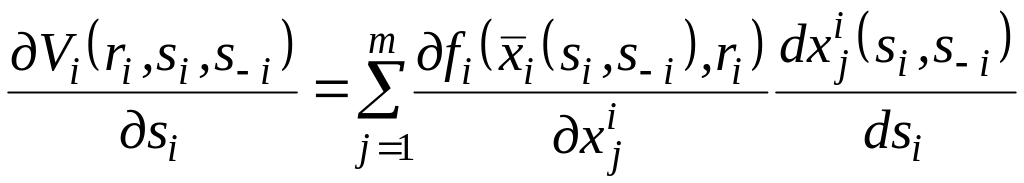З урахуванням умови (2.6) можна записати:

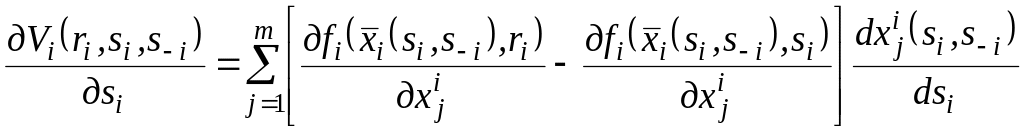. (2.12)

Знак лівої частини (2.26) визначається виразом:

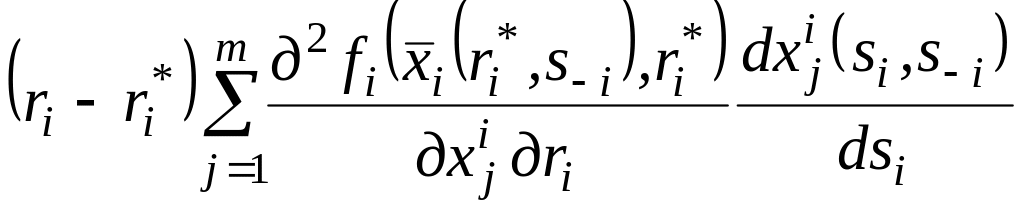, , (2.13)

звідки видно, що при виконанні умов Спенса—Мірліса та (2.11) функція не убуває при і не зростає при , тобто глобальний максимум будь-якої з функцій цілей досягається за умови , що і треба було довести.

Очевидно, (2.8) і (2.10) є необхідними умовами, а (2.11) достатньою умовою неманіпульованості механізму обміну. Вважаючи виконаними ці умови, розглянемо прибуток i-того виконавця у вигляді функції , яку називають «інформаційною рентою» виконавця.

З урахуванням (2.8) виконується умова

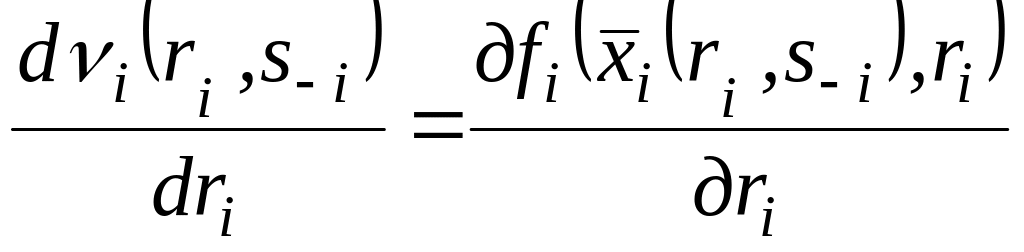. (2.14)

Згідно з першою умовою Спенса-Мірліса похідна (2.14) позитивна. Тоді інформаційна рента є зростаючою функцією від типу виконавця, тобто чим краще тип виконавця, тим більший прибуток він отримує від неповної інформованості GB щодо свого тип.

Оскільки умови індивідуальної раціональності не залежать від типу виконавця, можна нормалізувати мінімальний прибуток для кожного з виконавців і записати таким чином:

Отже, механізм керування слід створювати у такий спосіб, щоб прибуток будь-якого виконавця у разі, якщо його тип виявиться найгіршим із можливих для нього, був мінімальним, тобто не порушував вимог :

Таким чином, з урахуванням (2.14) маємо:

.

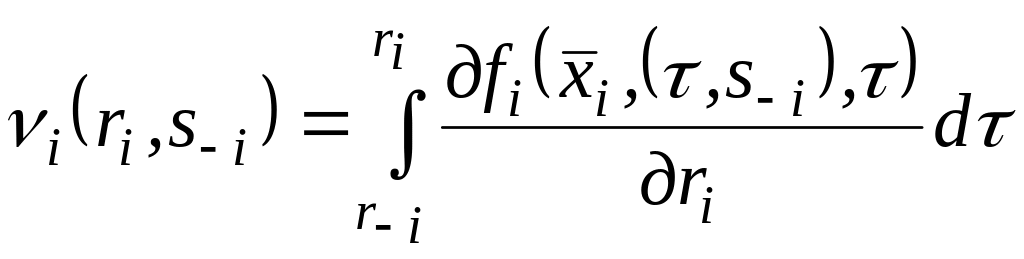Отримані результати дають змогу визначити сімейство механізмів, у яких домінантою стратегією виконавця є повідомлення істинних заявок. Завдання GB полягає у виборі з отриманого сімейства механізмів оптимального за заданим критерієм. Кінцеве рішення для кожної задачі залежатиме від виду критерію оптимальності, виду функцій корисності виконавців, обмежень на ресурси в системі, обмежень на взаємодії між виконавцями тощо.