2.2. Механізми планування розподілу ресурсу

Планування розподілу ресурсу є однією з найважливіших і найпоширеніших задач керування організаційною системою.

Стандартна постановка задачі розподілу ресурсу передбачає здійснення такого його розподілу між виконавцями, яке максимізувало б певний критерій ефективності (сумарну ефективність використання ресурсу виконавцями, прибуток організації тощо). Якщо ефективність використання ресурсу виконавцями невідома GB, то він змушений використовувати повідомлення виконавців щодо потрібних обсягів ресурсу. У разі дефіциту ресурсу виникає проблема маніпульованості — повідомлення виконавцями керівному органу недостовірної інформації.

Розглянемо постановку задачі розподілу ресурсу в дворівневій організаційній системі, що складається з GB і n виконавців (рис. 2.2).

Рис. 2.2. Система розподілу ресурсу

Для виконання замовленням на виробництво продукції GB має ресурс в обсязі R, який має бути розподілений між виконавцями, що мають цільові функції . Враховуючи, що обсяги виробничих ресурсів об’єктивно завжди обмежені, будемо розглядати випадок дефіциту ресурсу R, тобто . Крім того, вважатимемо, що на подані виконавцями заявки на ресурс GB накладає обмеження , а механізм розподілу ресурсу підкоряється таким цілком природним правилам:

1) ресурс розподіляється повністю, тобто (механізму розподілу ресурсу притаманна властивість збалансованості);

2) якщо виконавець одержав певну кількість ресурсу, то він завжди може, змінюючи тільки свою заявку, отримати будь-який менший його обсяг;

3) якщо кількість ресурсу, що розподіляє GB між усіма виконавцями, збільшується, то кожен виконавець за тим самим механізмом розподілу в рівновазі отримає ресурсу не менше, ніж при початковому механізмі.

Поділимо множину виконавців N на дві підмножини:

Q — підмножина виконавців, які отримують обсяг ресурсу менший за оптимальний, тобто , де — рівноважні повідомлення виконавців, при цьому ;

— підмножина пріоритетних виконавців, які отримують оптимальний для себе обсяг ресурсу, за що їх називають диктаторами [91].

Очевидно,  

Побудуємо відповідний прямий механізм, тобто механізм, який використовує повідомлені виконавцями оцінки { }. Для цього визначатимемо підмножину пріоритетних виконавців за такою процедурою.

Етап 1. GB припускає, що всі виконавці подали заявки на максимальні обсяги ресурсу, тобто при =  і Q = N визначені , де . Якщо , то : = .

Сутність цього етапу полягає в тому, що GB обчислює, скільки ресурсу отримає кожен виконавець, якщо всі вони повідомлять свої максимальні заявки. Якщо виконавець при цьому отримає більше ресурсу, ніж йому потрібно (більше за ), то надлишком ресурсу, який становить , він, за правилами 2 і 3, може поділитися з тими виконавцями, яким ресурсу бракує.

Етап 2. GB припускає і розподіляє між цими виконавцями ресурс , підставляючи у механізм розподілу ресурсу такі заявки виконавців з множини , щоб всі вони отримували оптимальну для себе кількість ресурсу (це можливо за другим правилом процедури розподілу ресурсу). Якщо з'являються нові пріоритетні виконавці, то їх включають у множину і повторюють етап 2. Це означає, що пріоритетним виконавцям виділяють оптимальну кількість ресурсу, а залишок поділяють між виконавцями, що не потрапили до числа пріоритетних.

Ця циклічна процедура збігається за кінцеву кількість етапів.

Прямий механізм, що визначають наведеною процедурою, використовує повідомлення { } і призводить до того самого розподілу ресурсу, що й початковий механізм. Більш того, за аналогією можна показати, що в прямому механізмі відсутнє маніпулювання, тобто повідомлення достовірної інформації виконавцями є рівновагою Неша [12]. Оскільки еквівалентний прямий механізм призводить до того самого розподілу ресурсу, що й початковий, то він має ту саму ефективність, що й початковий механізм.

Таким чином, для будь-якого механізму розподілу ресурсу, що задовольняє введеним припущеннями, існує еквівалентний прямий механізм не меншої ефективності. Отже, оптимальний механізм належить до класу неманіпульованих механізмів, тобто, будуючи механізм, в якому всі виконавці подають об’єктивні (правдиві) заявки на потрібний обсяг ресурсу, керівний орган не втрачає ефективності.

Залежно від постановки задачі існують різноманітні механізми розподілу ресурсів [14; 28; 84; 91]. Розглянемо деякі з них.

Механізми пріоритетного розподілу ресурсу. У механізмах пріоритетного розподілу ресурсу для формування плану (рішення щодо того, скільки ресурсу виділити тому чи іншому виконавцю) використовують умову:

(2.1)

де { } — множина заявок виконавців;

{ } — множина обсягів ресурсу, що виділяють виконавцям;

{ } — множина функцій пріоритетів виконавців;

— параметр нормування, що визначають таким, щоби при даних заявках і

функціях пріоритету в умовах дефіциту розподілявся в точності весь ресурс, тобто щоб виконувалася балансова умова:

= R. (2.2)

Друга складова умови (2.1) означає, що виконавець одержує ресурс в обсязі, що не більше від заявленої величини.

Окремим класом механізмів розподілу ресурсу є анонімні механізми, тобто механізми, в яких будь-яка перестановка виконавців не змінює призначених їм планів. Для механізмів розподілу ресурсу це означає, що в анонімному механізмі множини можливих повідомлень виконавців однакові, а процедура планування симетрична за їхніми заявками. При цьому будь-який анонімний механізм розподілу ресурсу еквівалентний механізму пропорційного розподілу. Справедливість цього твердження випливає з того факту, що будь-який анонімний механізм еквівалентний механізму послідовного розподілу ресурсу (див. далі), а механізм пропорційного розподілу є анонімним [84].

Пріоритетні механізми розрізняють залежно від виду функції пріоритету. До найуживаніших з них належать:

механізм прямих пріоритетів, в якому — зростаюча функція заявки , ;

механізм зворотних пріоритетів, в якому — убуваюча функція заявки , ;

механізм абсолютних пріоритетів, в якому пріоритети виконавців фіксовані і не залежать від повідомлених ними заявок, у зв’язку з чим будь-який механізм абсолютних пріоритетів позбавлений маніпулювання.

Механізм прямих пріоритетів. Якщо функції цілі виконавців є строго зростаючими функціями , тобто виконавці зацікавлені, щоб одержати максимально можливий обсягу ресурсу, то оскільки в механізмі прямих пріоритетів — зростаюча функція заявки , всі виконавці повідомлятимуть максимальні заявки на ресурс, керуючись принципом «більше просиш — більше матимеш».

Якщо функції переваги виконавців мають максимуми у точках { } , то аналіз дещо ускладнюється, проте якісний висновок залишається незмінним: за наявності найменшого дефіциту має місце тенденція до зростання заявок.

Ураховуючи, що функцією пріоритетів у цьому механізмі є заявка виконавця , підставимо її в умову (2.2) і визначимо параметр :

.

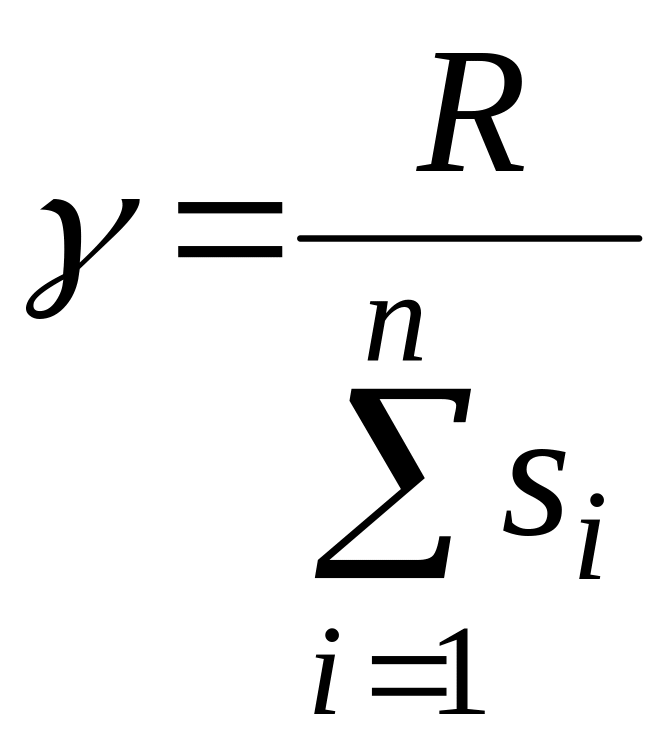Підставивши параметр у (2.1), матимемо формулу для розподілу ресурсу у механізмі прямих пріоритетів:

(2.3)

Розподіл ресурсу здійснюють пропорційно заявкам виконавців . Оскільки цільова функція виконавця є строго зростаючою, то всі виконавці повідомлятимуть максимальні заявки на ресурс. Якщо в системі задані обмеження на величину максимальної заявки , то всі виконавці в рівноважній ситуації заявлять величину . Це явище в економіці відомо як тенденція до завищення заявок на ресурси, що спричиняє появу штучного дефіциту.

Оскільки всі анонімні механізми прямих пріоритетів еквівалентні механізму послідовного розподілу ресурсу (ця властивість зумовлена тим, що, повідомляючи в анонімному механізмі однакові заявки, виконавці отримують однакові обсяги ресурсу), то для знаходження в них рівноважних заявок і рівноважного розподілу ресурсу GB може використовувати таку процедуру послідовного розподілу:

1) упорядкувати виконавців за зростанням повідомлених ними оцінок точок піку;

2) виділити всім виконавцям ресурс в обсязі, потрібному виконавцям з мінімальною точкою піку, якщо наявного ресурсу вистачає, в іншому разі — розподілити ресурс порівну і виключити виконавців з мінімальною точкою піку з розгляду;

3) виділити виконавцям, що не отримали ресурс, залишок його згідно з другим кроком.

Ця процедура прямого механізму розподілу ресурсу позбавлена маніпулювання, тобто повідомлення достовірної інформації є домінантною стратегією кожного з виконавців [84].

Недоліки механізму прямих пріоритетів:

існує тенденція до завищення заявок на ресурс, виконавцям вигідно сповіщати недостовірну інформацію;

невеликий дефіцит ресурсу породжує чималий штучний дефіцит.

Механізм зворотних пріоритетів. Механізм зворотних пріоритетів, в якому — убуваюча функція ( ), має низку переваг порівняно з механізмом прямих пріоритетів. Розглянемо механізм зворотних пріоритетів з функціями пріоритету вигляду:

,

де { } — множина величин очікуваного ефекту, що отримають виконавці від використання ресурсу.

Очевидно, відношення визначає питомий ефект від використання ресурсу . Тому механізм зворотних пріоритетів іноді називають механізмом

розподілу ресурсу пропорційно ефективності (ПЕ-механізмом).

Розглянемо приклад використання механізму зворотних пріоритетів. Нехай є три виконавця, для яких = 16, = 9, = 4, а їх метою є отримання максимального обсягу ресурсу. Треба визначити план розподілу керівним органом наявного ресурсу R = 18 між виконавцями.

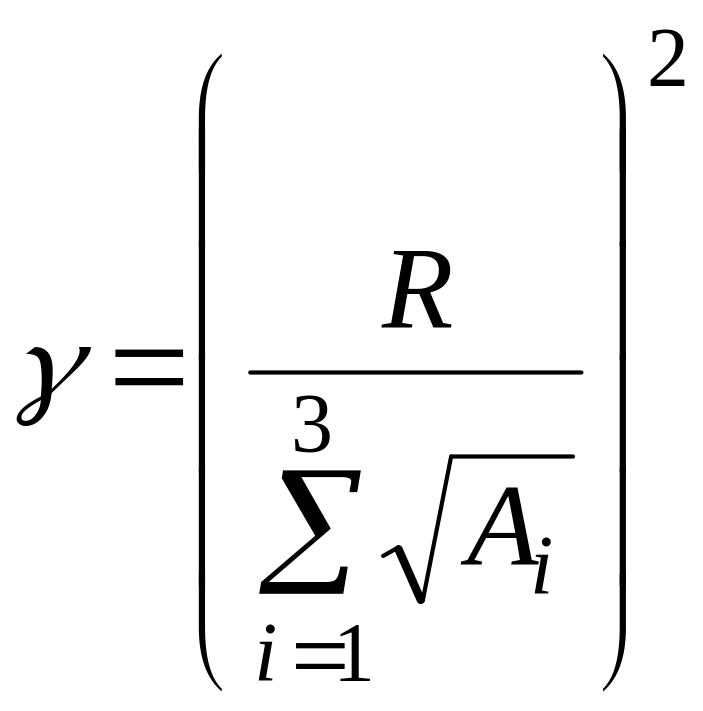Очевидно, максимумом функції є точка, що визначають з умови , тобто . Із балансового співвідношенням маємо = 4.

Отже, рівноважні заявки, що визначають за формулою 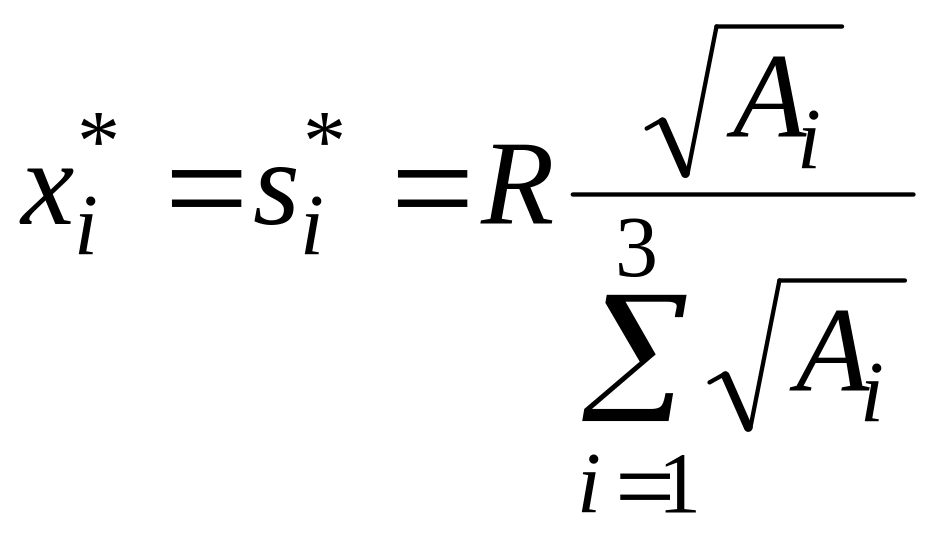, становлять

Отриманий розподіл ресурсу є рівновагою Неша. Дійсно, якщо перший виконавець зменшить свою заявку (наприклад, ), то . Отже, Якщо ж , то 4,5, а

Відомо, що визначені за механізмом зворотних пріоритетів рівноважні стратегії максимізують виграші виконавців за найгірших стратегій інших [9; 84]. При цьому якщо цільові функції виконавців мають піки (максимуми) в точках { } і якщо , то i-тий виконавець замовить рівно ресурсу і стільки ж його отримає тому, що у разі зменшення заявки його пріоритет зростає. Саме у такий спосіб визначають множину пріоритетних споживачів ресурсу.

Переваги механізму зворотних пріоритетів:

за рівноважної ситуації всі виконавці матимуть той обсяг ресурсу, який замовили; отже, сумарний попит дорівнює наявному обсягу ресурсу;

відсутня тенденція до завищення заявок на ресурс: всі виконавці замовляють не більше від оптимального обсягу.

Недоліками цього механізму є те, що за ним розподіл ресурсу не є оптимальним та втрачається інформація про реальні потреби в ресурсі.

Конкурсні механізми розподілу ресурсів. Конкурсні механізми розподілу ресурсу належать до пріоритетних механізмів, в яких на підставі певних процедур визначають переможців. Багатоманітного застосування набули конкурсні механізми, в яких виконавці беруть участь у змаганні на отримання ресурсу, пільгових умов фінансування, права на участь у виконанні замовлення, реалізації проекту тощо. Конкурс виконавців становить тендер на отримання ресурсу. Змагання між виконавцями сприяє підвищенню ефективності керування організаційною системою.

Процедура конкурсного механізму полягає в певному впорядкуванні виконавців на підставі інформації про них, якою володіє GB, а також інформації, яку вони самі повідомляють, з подальшим визначенням переможця (переможців) конкурсу. При цьому можливе спотворення виконавцями інформації (маніпулювання нею) з метою перемоги в конкурсі.

Розрізняють безперервні і дискретні конкурси. У першому з них претендент, отримуючи ресурс в обсязі, меншому від запитуваного, може мати відмінний від нуля ефект. Прикладом такої ситуації є пропорційна залежність між ефектом і ресурсом (ефективність постійна). У разі дискретних конкурсів

претенденту потрібен цілком певний обсяг ресурсу і будь-який менший обсяг його не задовольняє, оскільки призводить до нульового ефекту (наприклад, не дає змоги реалізувати проект, виробити продукцію тощо)

Розглянемо спочатку конкурсний механізм безперервного типу.

На відміну від механізму зворотних пріоритетів, де ресурс розподіляють пропорційно питомому ефекту його використання виконавцями, у конкурсному механізмі безперервного типу ресурс отримують тільки переможці тендеру (на всіх виконавців ресурсу може бракувати).

Після впорядкування виконавців за убуванням очікуваної ефективності ( ) GB розподіляє наявний ресурс у такий спосіб: виконавець, що має найочікуванішу ефективність, отримує ресурс у запитуваному обсязі, потім, якщо ресурс не закінчився, ресурс отримує наступний за визначеним порядком виконавець, і так продовжується до розподілу всього обсягу ресурсу. При цьому деякі виконавці можуть недоотримати заявлений обсяг ресурсу, але створити тим паче певний ефект, або взагалі не отримати його.

За такого розподілу ресурсу цілком імовірним виглядає поява випадків маніпулювання з боку виконавців. Тому за використання конкурсних механізмів керівний орган має організовувати дієву систему контролю за виконанням взятих зобов'язань. Такий контроль здійснюють шляхом введення системи штрафів:

, ,

пропорційних різниці між очікуваною і реальною ефективністю. Саме ця різниця характеризує величину маніпулювання, на яку свідомо йде виконавець задля отримання заявленого обсягу ресурсу і, отже, перемоги у конкурсі. На виконавця накладається штраф у тому разі, якщо , в іншому — штраф не накладається. Величину , що характеризує «силу» штрафу, визначає GB.

За цим механізмом цільова функція і-того виконавця має вигляд:

, ,

де — відсоток відрахувань від ефекту, що залишається у розпорядженні виконавця.

Очевидно, що перемога виконавця у конкурсі залежить від величини питомого ефекту і не залежить від обсягу заявки на ресурс . Тому виконавці будуть прагнути максимізувати свої цільові функції, тобто замовляти такий обсяг ресурсу, щоб у разі перемоги значення їх цільових функцій були максимальними. Можна стверджувати, що всі переможці конкурсу ( ) будуть мати однакові оцінки ефективності . Крім того, конкурсний механізм забезпечує оптимальний розподіл ресурсу [9].

Тепер розглянемо конкурсний механізм дискретного типу. Типовою задачею, що вирішують за допомогою цього механізму, є задача розподілу обсягу фінансування між виконавцями на реалізацію пакета інвестиційних проектів [14; 28; 94].

Для можливості вирішення цієї задачі треба мати дві оцінки:

експертну оцінку очікуваного ефекту від реалізації i-того проекту ( ), яку будемо вважати об’єктивною, хоча взагалі не можна виключати її свідоме завищення з боку експертів, зацікавлених у тому чи іншому проекті;

оцінку обсягу фінансування i-того проекту ( ), яку визначає організація, що його розробляє чи реалізує, і яка теж може бути завищеною.

Конкурсний механізм, що використовує ці оцінки, називають простим. За ним відбір проектів здійснюють на підставі їхньої упорядкованої черги за оцінкою ефективності, що залежить від наведених вище оцінок:

.

Цей відбір здійснюють доти, доки вистачає виділених інвестицій.

Якщо — множина проектів, відібраних до реалізації (переможців конкурсу), то загальний ефект становить

.

Відбір інвестиційних проектів, що забезпечать максимальний ефект від упровадження їх, здійснюють шляхом реалізації оптимізаційної моделі:

,

,

,

де R — загальний обсяг інвестицій, виділений на реалізацію проектів;

— об’єктивна оцінка обсягу фінансування i-того проекту.

Якщо — множина проектів, прийнятих до реалізації в результаті оптимального відбору, то загальний ефект становить:

.

Очевидно, .

Відношення визначає ефективність конкурсного механізму дискретного типу.

Експертний механізм розподілу ресурсу. У зв’язку зі складністю організаційної системи керівний орган має володіти чималими обсягами інформації, потрібної для прийняття ефективних управлінських рішень. Однак можливості такого органу обмежені, і він не завжди спроможний безпосередньо одержувати всю потрібну інформацію. Тому виникає потреба в отриманні інформації від експертів, що володіють знаннями у сфері діяльності конкретної організаційної системи.

Відома чимала кількість методів проведення опитувань експертів і опрацювання їх думок [29; 127]. Розглянемо лише одну з властивостей процедур експертного оцінювання, а саме — спотворення інформації виконавцями у механізмі розподілу ресурсу.

Із попереднього розгляду механізмів розподілу ресурсу відомо, що GB приймає управлінські рішення на підставі опитування (заявок) виконавців. Оскільки рішення, що приймає GB, безпосередньо зачіпає інтереси виконавців, то, швидше за все, кожен із них повідомить таку інформацію, яка приведе до прийняття найвигіднішого для нього рішення. Наприклад, якщо GB запитує у виконавців, який обсяг фінансових ресурсів потрібний їм для виконання певного проекту, навряд чи вони нададуть реальну інформацію про їх потреби, особливо у разі нестачі фінансів. Тому постає потреба в побудові процедури розподілу ресурсу, за якою виконавці не спотворювали б інформацію, яку надають керівному органу. У літературі таку процедуру називають механізмом активної експертизи [28; 91].

Розглянемо механізм активної експертизи на прикладі задачі розподілу ресурсу. Для визначення плану розподілу ресурсу GB залучає n експертів і кожному з них пропонує визначити величину ресурсу для i-того виконавця з відрізка [d, D], де d — мінімальна, а D — максимальна оцінка. Задача полягає у тому, щоб визначити план x розподілу ресурсу виходячи із заданих , .

Підсумкова оцінка , на підставі якої GB приймає рішення, є функцією оцінок, повідомлених експертами, . Позначимо через суб'єктивну думку i-того експерта, тобто його справжнє уявлення про обсяг ресурсу. При цьому вважається, що експерти повідомляють істинні оцінки. Якщо ж вони несвідомо помиляються, то середня оцінка є доволі об’єктивною і точною. Якщо експерти зацікавлені в результатах експертизи, то вони не обов'язково будуть повідомляти свою справжню думку, тобто механізм може бути підданий маніпулюванню ( ).

Кожен експерт зацікавлений у тому, щоб результат експертизи був максимально близький до його думки. Як цільову функцію i-того експерта приймають мінімум різниці між підсумковим рішенням x і його оцінкою :

, .

При цьому експерт повідомлятиме оцінку , що доставляє мінімум виразу:

.

Опишемо механізм отримання експертної оцінки x, який є механізмом відкритого керування [12; 116]. Вважатимемо, що оцінки експертів розташовані за неубуванням:

.

Обчислюють n допоміжних чисел, які поділяють відрізок [d, D] на n рівних частин:

, .

З усіх вибирають найбільший, який і є підсумковою експертною оцінкою:

.

У цьому механізмі оцінки експертів рівнозначні. Натомість можна ввести в ньому вагові коефіцієнти, які враховуватимуть різну кваліфікацію експертів.

Механізми розподілу витрат. На відміну від механізмів розподілу ресурсу з метою забезпечення максимальної ефективності його використання цей механізм призначений для визначення розподілу витрат між виконавцями на виробництво або купівлю загального для системи продукту, від використання якого кожен із виконавців отримує певний дохід. Задача, що вирішують за допомогою цього механізму, є у деякому розумінні двоїстою до задачі розподілу ресурсу.

Використання цього механізму, як і механізмів розподілу ресурсу, породжує проблему маніпулювання. Справді, якщо GB знає «рівень задоволення» кожного з виконавців від використання продукту, то можна пропонувати різні принципи розподілу витрат — порівну, пропорційно потребі у використанні, за рівнем задоволеності тощо. Який із цих принципів є «найсправедливішим» — окреме питання. Але зазвичай потреби виконавців відомі тільки їм самим. А якщо витрати виконавця залежать від його повідомлень, які виконавців неможливо або вельми важко перевірити, то він, очевидно, намагатиметься максимально зменшити свої витрати і користуватися результатами за рахунок інших виконавців.

Розглянемо приклад. Організаційна система, до якої входять два виконавця, хоче придбати продукт вартістю Ц = 1. Доходи виконавців від використання ними продукту становлять . Оскільки , то придбання продукту є вигідним як виконавцям, так і ОС загалом. Треба визначити розподіл витрат на придбання продукту між виконавцями, тобто визначити і за умови, що . Такий розподіл може бути здійснений за різними принципами. Розглянемо їх.

Принцип рівного розподілу. Покладемо . Якщо значення цільових функцій

, і = 1,2

невід'ємні, то цей варіант допустимий (у нашому прикладі це не так). Наголосимо, що він є неманіпульованим (у виконавців нічого не питають — використовують принцип абсолютних пріоритетів). Однак не завжди принцип рівного розподілу є «справедливим». Справді, якщо апріорі відомо, що , що має місце у прикладі, то буде неправильно змушувати виконавців платити порівну.

Принцип пропорційного розподілу. За цим принципом використовують правило: «кому продукт потрібніший, нехай той більше й платить». Тому розподілимо витрати пропорційно доходу:

, і = 1,2,

де , а — оцінка доходу, що сповіщає і-тий виконавець.

Очевидно, , позаяк, якщо сумарний дохід менше від витрат, то придбання продукту невигідне ОС. Для того щоб цільові функції були невід'ємними, вимагатимемо виконання нерівностей , які задають допустиму область заявок виконавців. Цілком зрозуміло, що за такої ситуації обидва виконавці будуть намагатися знизити заявки. При цьому рівновагою Неша буде множина пар заявок , що становлять відрізок прямої .

Очевидно, цей принцип є принципом рівних рентабельностей [69]. Справді, враховуючи, що рентабельність і-того виконавця визначають як відношення прибутку до витрат, тобто

,

із процедури пропорційного розподілу випливає, що .

Принцип рівних прибутків. Якщо механізм розподілу витрат має вигляд

,

то множина рівноваг Неша є тією самою, що й у принципі пропорційного розподілу.

Наведені принципи розподілу витрат можна легко узагальнити в разі будь-якої кількості виконавців [9; 15; 72; 123; 124].