
- •1. Разрушение горных пород в условиях высоких температур
- •1.1. Кинетические концепции в механике
- •1.2. Разрушение горных пород при высоких температурах
- •1.3. Связь энергии активации разрушения с термодинамическими параметрами породообразующих минералов
- •1.4. Высокотемпературные реакции в породообразующих минералах. Плавление твердых тел
- •2. Электротермическое разрушение горных пород
- •2.1. Физические основы электротермического разрушения горных пород
- •2.2. Разрушение породы тепловым пробоем
- •2.3. Разрушение горных пород диэлектрическим нагревом
- •2.4. Разрушение горных пород на сверхвысоких частотах
- •2.4.1. Разрушение горных пород в стоячей электромагнитной волне
- •2.4.2. Отбойка горных пород сверхвысокими частотами
- •3. Физические основы электрического разряда в жидкости и оборудование разрядно-импульсной технологии
- •3.1. Общие сведения об электрическом разряде в жидкости
- •3.2. Оборудование в разрядно-импульсной технологии и технологический узел
- •3.2.1. Генератор импульсных токов
- •3.2.2. Технологический узел
- •3.2.3. Электроимпульсные установки
- •4. Основы разрядно-импульсной технологии разрушения минеральных сред
- •4.1. Механизм разрядно-импульсного разрушения и рациональные области применения разрядно-импульсной технологии
- •4.2. Теоретические основы разрядно-импульсного разрушения мин еральньгх сред
- •4.3. Условие разрядно-импульсного разрушения минеральных сред, действующие факторы и показатели
- •4.4. Теоретические основы разрядно-импульсной технологии
- •4.5. Управление разрядно-импульсным воздействием
1. Разрушение горных пород в условиях высоких температур
1.1. Кинетические концепции в механике
ДЕФОРМИРОВАНИЯ И РАЗРУШЕНИЯ ГОРНЫХ ПОРОД
Обширный экспериментальный материал, обобщенный в ряде крупных монографий, а также исследования последних лет охватывают широкий диапазон термодинамического воздействия на горные породы в интервале давлений до 103 МПа и, температур, превышающих 1000 К, включая широкое варьирование условиями сложнонапряженного состояния и скоростью нагружения.
Использование оптической микроскопии, а в последние десятилетия рентгеноструктурного анализа и электронной фрактографии (включая растровую) значительно расширило представления о механике деформирования и разрушения горных пород в условиях статических и динамических нагрузок.
Вместе с тем, в механике деформирования и разрушения горных пород, как и металлов, керамик, полимеров и т.д., общая цель состоит в том, что для всех материалов необходимо связать макроскопические критерии текучести и разрушения с явлениями на микроскопическом уровне.
На обширном экспериментальном материале было установлено, что время до разрушения различных материалов зависит от величины нагрузки, скорости нагружения и температуры окружающей среды. Эмпирическая зависимость долговечности от температуры и „величины приложенной постоянной нагрузки — уравнение долговечности, предложенное акад. С.Н. Журковым, имеет вид


 (1.1)
(1.1)
где
 =
=
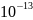 с
— коэффициент численно равный периоду
тепловых колебаний атомов в
кристаллической решетке; (U0
— энергия активации разрушения;
с
— коэффициент численно равный периоду
тепловых колебаний атомов в
кристаллической решетке; (U0
— энергия активации разрушения;
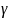 —
структурный коэффициент;
—
структурный коэффициент;
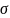 —
действующее растягивающее напряжение;
R
— универсальная-
газовая постоянная; Т
— абсолютная
температура. Зависимость времени "жизни"
материала
—
действующее растягивающее напряжение;
R
— универсальная-
газовая постоянная; Т
— абсолютная
температура. Зависимость времени "жизни"
материала
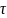 от
температуры Т
трактуется
как термофлуктуационный процесс
разрушения межатомных связей.
от
температуры Т
трактуется
как термофлуктуационный процесс
разрушения межатомных связей.
По аналогии с уравнением долговечности эмпирически установлено, что при постоянной скорости деформирования « выполняется соотноше ние»
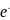 =
=
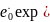
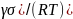 (1.2)
(1.2)
где
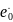 =
=
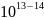
 — эмпирический коэффициент.
— эмпирический коэффициент.
Используя
принцип суммирования повреждений,
накапливающихся в материале под
действием изменяющейся во времени
нагрузки
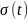 (принцип
Бейли), долговечность материала может
быть определена из уравнения
(принцип
Бейли), долговечность материала может
быть определена из уравнения
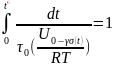 (1.3)
(1.3)
где t* — время до разрушения.
Перспектива и необходимость использования кинетических концепций при описании деформационных и прочностных свойств горных пород и породных массивов отмечены акад. М.А. Садовским. Это в полной . мере относится и к изучению деформационно-прочностных свойств горных пород в условиях высоких температур, природа и механизм термофлуктуационного накопления поврежденности которых изучены далеко не полно.
Процессы ползучести горных пород традиционно связаны с механизмом развития пластического течения, а точнее диффузионно-вязкого или дислокационно-вязкого течения, обусловленного перемещением дефектов в кристаллах под воздействием внешних механических напряжений. Причем, предпочтение отдается диффузионным процессам, протекающим в объеме минерального зерна и объясняющим интегральный эффект деформации макрообмена как совокупности объемов минеральных фаз.
Близость энергии активации процесса пластического течения к энергии самодиффузии в металлах, и, как это показано в работе [41], аналогичная закономерность свойственна и некоторым разновидностям горных пород, являются экспериментальным подтверждением диффузионно-вязкой концепции процесса деформации.
Вместе с тем, надмолекулярная структура минеральных фаз, выявленная в частности методами электронной микроскопии, и поведение зерна как индивидуального элемента гетерогенной среды в поле механических напряжений, включая остаточные напряжения в минералах и горных породах, до сих пор не нашли отражения в аналитическом описании процессов деформирования и разрушения горных пород.
Известны примеры использования уравнения Надаи для описания процессов деформирования в приложении к горным породам. Так, хорошее соответствие уравнения Надаи с результатами экспериментов получено при изучении процесса деформирования образцов гипса. Установившаяся скорость деформирования ё удовлетворительно описывается уравнением
=
sinh[(Δ ]
(1.4)
]
(1.4)
где
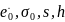 - эмпирические "постоянные".
Эмпирические "постоянные" в
уравнении скорости деформирования
являются в сущности коэффициентами
математической аппроксимации
экспериментальных данных и не несут
физическую смысловую нагрузку.
- эмпирические "постоянные".
Эмпирические "постоянные" в
уравнении скорости деформирования
являются в сущности коэффициентами
математической аппроксимации
экспериментальных данных и не несут
физическую смысловую нагрузку.
Таблица 1. Значения энергии активации (U0 и коэффициента п (по данным зарубежных исследователей)
Порода |
n |
|
Кварцит (влажный) 2,6 ±0,4 231 ± 28
Кварцит (сухой) - 269 ± 23
Оливин (сухой) 3,6 399
Дунит (влажный) - 395 ± 12
Дунит (сухой) - 529
Энстатит (сухой) 3 273
Ангидрит (сухой) - 151 ±8
Естественное стремление связать процесс деформирования горных пород с параметрами кристаллических решеток породообразующих минералов нашло отражение в ряде опубликованных работ.
Уравнения, предложенные Лекомтом
R
lg
(
/
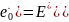 (1 .5)
(1 .5)
и Эйрингом, Ри и др.:
=
exp[-Е*/(RT)
] sinh [(Δ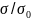 )
(1.6)
)
(1.6)
содержат энергию активации Е*, определяющую энергетический барьер сопротивления элементарного объема кристаллической решетки развитию пластического течения и разрушения. Значения энергии активации для каменной соли порядка 126 кДж/моль, полученное по формуле (1.5), и для мрамора порядка 252 кДж/моль по формуле (1.6) близки к значению энергии самодиффузии атомов в галите и кальците. Для описания процесса установившейся скорости деформирования горных пород применяется выражение вида
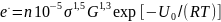 (1.7)
(1.7)
где п — эмпирический коэффициент; G- модуль сдвига.
Значения энергии активации и коэффициента п для некоторых разновидностей сухих и влажных горных пород приведены в табл. 1.
Для описания процесса деформирования поликристаллических агрегатов ферстерита в диапазоне температур до 1900 К использовано кинетическое уравнение
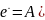
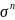 /
/ )exp
)exp
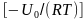 (1.8)
(1.8)
где
d
—
размер зерен;

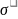 — разность напряжений; А
—
эмпирическая константа материала. На
стадии установившейся ползучести при
температуре Т=
1873
К n=1,
m=
1,5
± 0,5.
— разность напряжений; А
—
эмпирическая константа материала. На
стадии установившейся ползучести при
температуре Т=
1873
К n=1,
m=
1,5
± 0,5.
Процесс деформирования известняка и мрамора при высоких температурах удовлетворительно описывается уравнением
e=
 exp[-100/(RT)]
exp[-100/(RT)]

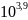 exp[-102/(RT)
exp[-102/(RT)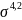 (1.9)
(1.9)
Приведенные выражения (1.5) —(1.9) являются модификациями уравнения Френкеля— Эйринга, записываемого в виде
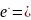 Ф
(
)
exp
(1.10)
Ф
(
)
exp
(1.10)
где Ф ( ) — некоторая функция действующего напряжения.
Детальные исследования применимости уравнения (1.2) для описания процесса деформирования и разрушения горных пород при широком варьировании режимов нагружения и изменения влажности выполнены проф. АН. Ставрогиным с сотрудниками. В этих исследованиях показано, что в условиях сдвигового пластического деформирования энергия активации близка по величине к энергии самодиффузии атомов в минералах типа NаС1 и СаС03. При отрыве энергия активации приближается к энергии сублимации.
Дислокационный механизм использован Байтом для описания процесса деформации кварцита. Для описания скорости сдвиговых деформаций использовано выражении
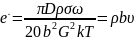 (1.11)
(1.11)
где
р — плотность подвижных дислокаций; b
—
вектор Бюргерса;
 —
скорость дислокаций; D
—
коэффициент диффузии;
—
действующее напряжение; G
—
модуль сдвига; k
—
постоянная Больцмана; T
—абсолютная температура;
—
скорость дислокаций; D
—
коэффициент диффузии;
—
действующее напряжение; G
—
модуль сдвига; k
—
постоянная Больцмана; T
—абсолютная температура;
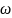 —
константа материала.
—
константа материала.
D=
5
 exp[-
exp[-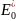 /(RT)]
/(RT)]
где
-
энергия диффузии (для кварца
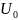 = 34 кДж/моль).
= 34 кДж/моль).
На рис. 1 показаны кривые ползучести каменной соли в диапазоне температур до 500 К. При этом для описания процесса ползучести использовалось аппроксимирующее уравнение
e(t)
= 5

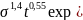
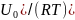 (1.12)
(1.12)
где 1/0 — энергия активации ползучести (для каменной соли ?/« = 83 кДж/моль).
К. Фергнсон, используя экспериментальные результаты исследования ползучести известняков в условиях высоких температур, применил уравнение для описания скорости ползучести от температуры вида:
=A
exp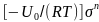 (1.13)
(1.13)
В частности, для одной из моделей значения входящих параметров в уравнение (1.13) следующие: A= , ( = 419 кДж/моль, п = 4,2.)
Феноменологический подход к описанию процесса деформирования, включающий в том или ином виде функцию [ / (RТ), отражает фундаментальный процесс накопления повреждений в материале под дей- ствием внешней нагрузки и температуры.
-

Рис. 1. График ползучести каменной соли: кривые1, 2 и 3 — соответствуют дифференциальному давлению 10,5 МПа при температуре соответственно 473, 443 и 388 К; 4 и 5 — 20,7 МПа при температуре соответственно 388 и 353 К
Причем, чем выше значение энергии активации разрушения материала , тем меньше скорость протекания процессов деструкции при заданном давлении и температуре Ассоциативная связь между энергией активации разрушения и энергией самодиффузии и сублимации дает основание для предположения ( развитии термофлуктуационных процессов разрыва "связей" в процесс* деформирования горных пород.
Экспериментальным подтверждение!» является регистрация акустической эмиссии при деформировании образцов горных пород во времени под действием постоянной нагрузки. Ус тановившаяся скорость накопления дефектов «описывается уравнением
![]() (1.14)
(1.14)
где n0 — эмпирический коэффициент [43].
Несмотря на разнообразие эмпирических уравнений, используемы для описания процессов деформирования горных пород в условия: высоких температур, термофлуктуационная концепция накопления поврежденности в горных породах качественно правильно отражав закономерности развития процесса деформирования и разрушения горных пород различных генетических групп.

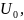 кДж/моль
кДж/моль