ФЕДЕРАЛЬНОЕ
АГЕНТСТВО СВЯЗИ
Федеральное государственное образовательное бюджетное
учреждение высшего профессионального образования
«САНКТ-ПЕТЕРБУРГСКИЙ
ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ
им. проф. М. А. БОНЧ-БРУЕВИЧА»
___________________________________________________________________________
П.З. Мкртычян.
МАТЕМАТИКА
ТЕОРИЯ ПРЕДЕЛОВ
УЧЕБНО-МЕТОДИЧЕСКОЕ ПОСОБИЕ
ПО ВЫПОЛНЕНИЮ СОМОСТОЯТЕЛЬНОЙ РАБОТЫ
СПбГУТ )))
САНКТ-ПЕТЕРБУРГ
2015
УДК
ББК
Рецензент
заведующий кафедрой Высшей математики ПГУПС
кандидат физ.-мат. наук, проф. Гарбарук В.В.
Утверждено редакционно-издательским советом СПбГУТ
в качестве методических указаний
|
Мкртычян П.З. |
|
Математика. Теория пределов. Методические указания / П.З. Мкртычян . – СПб.: Издательство СПбГУТ, 2014.
В методических указаниях подробно представлены необходимые теоретические положения теории пределов, в том числе, и правило Лопиталя раскрытия неопределённостей, подробно разобрано большое количество примеров. Методические указания содержат 25 вариантов контрольных работ на вычисление пределов. Данное издание можно использовать для самостоятельного освоения студентами-бакалаврами технических специальностей практической части указанного раздела высшей математики.
|
УДК
ББК
© Мкртычян П.З. 2014
© Федеральное государственное образовательное бюджетное учреждение высшего профессионального образования «Санкт-Петербургский государственный университет телекоммуникаций им. проф. М. А. Бонч‑Бруевича».
-2-
Содержание
1.Некоторые необходимые обозначения и определения………………………………4
2.Определения пределов…………………………………………………………………………………6
3.Основные теоремы о пределах. Правила вычисления пределов……………….12
4.Непрерывные функции…………………………………………………………………………………14
5.Замечательные пределы……………………………………………………………………………….15
6.Сравнение бесконечно малых. Принцип эквивалентности…………………………17
7.Вычисление пределов…………………………………………………………………………………..19
8.Вычисление пределов по правилу Лопиталя……………………………………………….26
9.Варианты контрольных заданий…………………………………………………………………..29
10.Литература……………………………………………………………………………………………………41
-3-
1.Некоторые необходимые обозначения и определения.
Понятие предела является одним из основных понятий математического анализа.
Прежде, чем дать определение предела, приведём некоторые необходимые обозначения и определения.
Множество
всех вещественных чисел будем обозначать
через R.
Следующие
значки означают: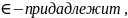
не принадлежит,
содержится,
любой,
существует,
следует,
тогда и только тогда. Заглавными буквами
A,B
и т.д. будем
обозначать множества вещественных
чисел ( т.е. A
,
B
),
а малыми буквами a,
b
и т.д. их
элементы (a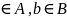
).
Определение
1.1.
-окрестностью
точки
R
называется
множество
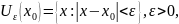т.е. множество, состоящее из всех тех
чисел
,
которые удовлетворяют неравенству
.
Нетрудно понять, что
.
Определение
1.2.
-окрестностью
«плюс бесконечности» (+
называется множество
=(
Определение
1.3.
-окрестностью
«минус бесконечности»
(
называется множество
=(
Определение
1.4.
-окрестностью
« бесконечности»
(
называется множество
=(
(
Заметим,
что предполагается
только в определении 1.1. Если в
Определение
1.5. Точка
называется внутренней
точкой множества A
,
если она принадлежит множеству A
вместе с
некоторой своей
-окрестностью.
Определение 1.6. Множество A называется открытым, если все его точки внутренние.
Пример 1.1.Всякий открытый интервал (a,b) является открытым множеством.
-4-
Определение
1.7. Окрестностью
точки
называется всякий открытый интервал
(a,b),
содержащий
точку
Заметим, что -окрестность точки является также её окрестностью.
Определение 1.8. Точка называется граничной точкой множества A , если всякая её окрестность содержит как точки, принадлежащие множеству A, так и не принадлежащие ему.
Заметим, что граничная точка может принадлежать множеству, а может и не принадлежать ему.
Пример
1.2. Граничными
точками множества A=
являются точки a
и b,
но точка a
принадлежит множеству A,
а b
не принадлежит
ему.
Определение
1.9. Объединение
множества А
с множеством
его граничных точек называется замыканием
множества
А и
обозначается
.
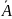Определение 1.10. Если А= , то множество А называется замкнутым.
Пример
1.3.
,
,
.
Определение 1.11. Точка называется предельной точкой множества А, если любая её окрестность содержит точку множества А, отличную от точки .
Заметим, что предельная точка множества может принадлежать этому множеству, а может и не принадлежать ему; точка, принадлежащая множеству, может не быть его предельной точкой.
Определение 1.12. Точка называется изолированной точкой множества А, если она принадлежит множеству А и не является его предельной точкой.
Пример
1.4. Пусть
А=(0,1)
.
Предельными точками множества А
являются только и только все точки
интервала [0,1]; точка x=2
является изолированной точкой множества
А.
Пример
1.4. Все точки
множества натуральных чисел N={1,2,3,…}
являются изолированными. У множества
N
есть только одна предельная точка +
-5-