5  Уширитель

Характеристики прочности принимают по таблице 3.3 [41]. Заметим, что при использовании данных таблицы 3.3 удельное сцепление грунта иногда оказывается завышенным.

Таблица 3.3.  Значения прочностых характеристик грунта в зависимости от удельного сопротивления погружению зонда

qс, МПа	c, кПа	, 	qс, МПа	c, кПа	, 
0,5	18	16	3,5	53	23
1,0	24	17	4,0	58	24
1,5	30	18	4,5	64	25
2,5	36	19	5,0	70	26
2,5	41	20	5,5	76	27
3,0	47	22	6,0	82	28

При динамическом зондировании измеряется глубина погружения зонда от одного или нескольких ударов или подсчитывается число ударов, необходимое для погружения зонда на заданную глубину (обычно на 10 см погружения зонда). Затем по эмпирическим зависимостям определяют динамическое сопротивление грунта и от него переходят к определению деформационных и прочностных характеристик.

4. Теория линейно-деформируемой среды

4.1. Три фазы деформирования грунта по Н.М. Герсеванову

Переходя к задачам определения напряженно-деформированного состояния основания, обратимся к принципиальному опыту, иллюстрирующему работу грунта в основании фундаментов.

Предположим, что на горизонтальном основании находится жесткий штамп (рис. 4.1), на который действует сила P. По мере увеличения нагрузки будем измерять осадку штампа s. Предположим также, что нагрузка увеличивается достаточно медленно или подается ступенями, причем после каждой ступени выжидают стабилизацию деформаций основания. В результате построим график зависимости s(P)  график «осадка-нагрузка» (рис. 4.2)  и проанализируем характер полученной кривой.

Рисунок 4.1.  Принципиальная схема опыта со штампом на грунтовом основании

Рисунок 4.2.  Зависимость осадки основания от нагрузки на штамп (график «осадка-нагрузка»). I  фаза уплотнения, II  фаза локальных сдвигов, III  фаза разрушения

На первом участке OA график линейный или близок к линейному. После превышения нагрузкой P некоторого значения P_1кр  первой критической нагрузки  на участке AB зависимость s(P) приобретает ярко выраженный нелинейный характер. В конце этого участка кривая становится практически параллельной оси Os, т.е. малым приращениям внешней нагрузки соответствует значительный рост деформаций основания. Эту нагрузку обычно называют второй критической нагрузкой P_2кр или предельной нагрузкой P_u. Таким образом, по Н.М. Герсеванову (1930 г.) выделяют три фазы деформирования грунта:

• фаза уплотнения (0 < P  P_1кр);

• фаза локальных сдвигов (P_1кр < P < P_2кр);

• фаза разрушения (P  P_2кр).

Теперь рассмотрим несколько подробней, что происходит в грунте на протяжении данного опыта.

В первой фазе деформирование грунта идет, в основном, за счет уплотнения грунта, уменьшения объема пор. Частицы грунта перемещаются преимущественно вниз. При достижении нагрузкой значения P_1кр под краями и на некоторой глубине под центром штампа начинают зарождаться зоны предельного напряженного состояния. Деформации грунта в фазе уплотнения  затухающие.

Во второй фазе все большее количество точек грунта переходит в предельное напряженное состояние, идет образование так называемого «уплотненного грунтового ядра» под штампом. Деформирование преимущественно происходит уже за счет пластических сдвигов, повсеместно возникающих в основании. Ближе к завершению фазы намечаются общие поверхности скольжения. Деформации грунта в фазе локальных сдвигов уже могут быть и незатухающими.

При достижении третьей фазы наблюдается выпирание грунта из-под подошвы штампа по криволинейным поверхностям скольжения, составляющим у верхней границы основания острый угол с горизонталью (рис. 4.3). Это сопровождается значительным нарастанием осадок, а штамп непрерывно погружается в основание практически без увеличения нагрузки. Деформации грунтов в фазе разрушения всегда незатухающие. Этот момент означает потерю устойчивости основания.

Рисунок 4.3.  Принципиальная схема разрушения грунта в основании штампа

Следует заметить, что характер деформирования грунта в рассматриваемом опыте существенно зависит от условий опыта, в первую очередь, от глубины заложения штампа и от вида грунта. Так, для заглубленных штампов при достижении предельной нагрузки выпирания грунта на поверхность не происходит, а области предельного напряженного состояния, где наиболее интенсивно развиваются процессы пластического течения грунта, формируются у боковых граней штампа. В случае песчаных оснований зависимость осадки от нагрузки заметно дольше сохраняет линейность, чем у глинистых грунтов, и переход к фазе разрушения осуществляется сравнительно быстро, а на графике «осадка-нагрузка» для пластичных и текучих глинистых грунтов иногда бывает вообще трудно выделить линейный участок. Вместе с тем, описанная картина изменения напряженно-деформированного состояния основания отвечает общей схеме работы оснований фундаментов и служит отправной точкой при создании многих расчетных схем и моделей грунта.

Итак, обратимся к основным теоретическим методам определения напряжений и деформаций в основании при вдавливании в него штампа. Для математического описания поведения грунта в первой фазе деформирования наибольшее распространение получила теория линейно-деформируемой среды (ТЛДС). По сути, эта теория представляет собой совокупность ряда решений теории упругости, которые возможно применить для грунтовых сред. Напомним (см. п. 3.2.1), что грунты, строго говоря, не обладают упругостью, т.е. полностью не восстанавливают форму после снятия нагрузки. Однако было доказано (Н.М. Герсеванов, Н.П. Пузыревский, В.А. Флорин и др.), а затем подтверждено строительной практикой, что для описания работы грунта в фазе уплотнения допустимо использовать некоторые положения теории упругости. Как отмечалось в п. 3.2.1, обобщенный закон Гука в определенном интервале давлений и гипотезу малости деформаций можно считать справедливыми, а грунт допустимо рассматривать как сплошное, а не дискретное тело. Отклонения получаемых по ТЛДС напряжений и осадок от наблюдаемых в натуре становятся существенными только во второй фазе деформирования грунта, которую рассмотрим чуть позже.

Фаза разрушения грунта описывается приближенными и точными решениями, которые объединены в теорию устойчивости грунтов. В основе решений теории устойчивости обычно лежит закон Кулона. При этом полагают либо, что каждая точка грунта находится в предельном равновесии, либо, что одна часть грунта, принимаемая, как правило, жесткой, смещается по некоторой поверхности сдвига относительно неподвижной части основания. Особо отметим теорию предельного равновесия грунтов (ТПРГ), которая рассматривает точные решения.

Для расчетов грунтовых оснований в фазе локальных сдвигов применяют упругопластический анализ деформирования грунтовых массивов, иногда рассматриваемый как раздел теории устойчивости. Упругопластический анализ отличается наиболее общей постановкой, где учитывается, что некоторые области грунта еще находятся в допредельном напряженном состоянии, и деформируются согласно закону Гука, а при достижении в какой-либо точке предельного равновесия, деформирование грунта в этой точке подчиняется законам пластического течения (см. п. 3.2.3). При этом с ростом нагрузок увеличиваются и размеры пластической области.

В заключение еще раз подчеркнем, что понятие о фазах деформирования грунта во многом является ключевым для описания работы оснований сооружений.

4.2. Постановка плоской и пространственной задач теории линейно-деформируемой среды

4.2.1. Пространственная и плоская задачи

Как известно, в различных разделах механики выделяют три типа задач [2]: пространственное напряженное состояние (рис. 4.4, а), плоское напряженное состояние (рис. 4.4, б) и плоское деформированное состояние (рис. 4.4, в). В случае пространственной задачи напряжения и деформации среды возможны во всех направлениях. Плоское напряженное состояние подразумевает отличные от нуля значения напряжений, действующих только в одной плоскости xOz, а деформирование среды возможно во всех трех плоскостях. Плоская деформация предполагает невозможность деформирования тел в направлении, перпендикулярном рассматриваемой плоскости xOz, в то время как напряжения в этом направлении ненулевые. Поскольку грунт практически не работает на растяжение и не может держать форму, аналогичную показанной на рис. 4.4, б, очевидно, что для грунта смысл имеют только пространственный случай и плоская деформация, которую в дальнейшем для краткости будем иногда называть просто плоской задачей.

Рисунок 4.4.  Виды напряженного состояния: а  пространственное напряженное состояние; б  плоское напряженное состояние; в  плоское деформированное состояние

Плоские схемы, безусловно, являются идеализацией реальных оснований и конструкций. Однако большое количество практических задач без сколько-нибудь значительных погрешностей решают в плоской постановке, причем задачи геотехники зачастую даже лучше, чем надземные конструкции, отвечают условиям плоской задачи как, например, основание ленточного фундамента, откосы и склоны, подпорные стенки, железнодорожные и автодорожные насыпи, тоннели, плотины и т.д.

В бесконечно длинном теле, находящемся в условиях плоской деформации, все поперечные сечения равноправны: во всех сечениях картина напряженно-деформированного состояния одинакова и связана с координатами x и z, но не зависит от координаты у. Поэтому при исследовании какой-либо задачи о плоской деформации можно рассматривать участок тела любой длины. Практически удобно рассматривать участок длиной, равной единице ее измерения, например, участок длиной в 1 м.

Если тело (исследуемая область основания или конструкция) имеет конечную длину, то с известной степенью точности плоская деформация будет иметь место в среднем участке тела, а при удалении от центра условия плоской деформации будут выполняться все хуже. На концевых участках и в их окрестностях напряженно-деформированное состояние будет пространственным.

Заменой пространственной схемы на плоскую для тел конечной длины широко пользуются на практике. Это вызвано тем, что в подавляющем большинстве случаев постановка и решение плоских задач оказывается намного проще, чем пространственных, у которых это иногда наталкивается на принципиальные трудности. Поэтому в дальнейшем чаще всего сначала будем рассматривать плоскую задачу, а затем делать обобщения на пространственный случай.

4.2.2. Основные гипотезы

Перечислим основные гипотезы теории линейно-деформируемой среды:

1. Основание находится в равновесии. Необходимость введения этой гипотезы очевидна, в противном случае грунт будет двигаться с ускорением, что недопустимо для большинства инженерных строительных задач.

2. В заданном диапазоне напряжений поведение грунта подчиняется обобщенному закону Гука, что следует из физической сути исследуемого явления  характера деформирования грунта в фазе уплотнения. Иначе эту гипотезу формулируют как принцип линейной деформируемости (см. п. 3.2.1).

3. Перемещения точек грунта малы по сравнению с конечными размерами сооружения. Это допущение справедливо для многих задач геотехники и очень важно, поскольку (в совокупности с гипотезой 2) обеспечивает применимость в решениях ТЛДС принципа суперпозиции или принципа независимости действия сил.

4. Грунт считается однородным и изотропным. Данное допущение в общем случае не обязательно. Существуют исследования, в которых подробно разработаны методы решения задач для неоднородных и анизотропных материалов, однако ниже будет рассматриваться преимущественно простейшая среда.

5. Грунт рассматривается как сплошное тело. Крайне важная гипотеза, на основании которой возможно использовать аппарат дифференциального и интегрального исчислений, основанных на анализе бесконечно малых величин.

4.2.3. Постановка плоской задачи

Аналогично задачам линейной теории упругости [2] рассмотрение задач ТЛДС включает в себя: статическую сторону задачи  уравнения равновесия, выражающие гипотезу 1; физическую сторону  связь между напряжениями и деформациями  обобщенный закон Гука (гипотеза 2); геометрическую сторону  уравнения, связывающие перемещения точки с деформациями, при составлении которых воспользуемся гипотезой 3.

Статическая сторона задачи. Согласно гипотезе 1 грунт должен находиться в равновесии. Соответственно в равновесии должна находиться и каждая его частица. Рассмотрим схему напряженного состояния грунта в точке в декартовой системе координат xOz (рис. 4.5). Следует иметь в виду, что, в отличие, например, от «Сопротивления материалов» в механике грунтов принято считать сжимающие напряжения положительными.

Рисунок 4.5.  Схема напряженного состояния в точке (плоская задача, декартовы

координаты)

Размеры выделенного из тела бесконечно малого элемента грунта составляют dx и dz вдоль соответствующих осей. Размер элемента в направлении, перпендикулярном рассматриваемой плоскости примем равным единице. В общем случае напряжения на противоположных гранях элемента будут иметь различные значения. В силу малости размеров элемента они будут отличаться на бесконечно малые величины. Если на ближних к координатным плоскостям гранях элемента действуют напряжения _x, _z, _xz  _zx (в силу парности касательных напряжений), то на противоположных гранях они изменятся на величину своих частных дифференциалов по соответствующим осям:

, , , ,

где , , ,  бесконечно малые приращения соответствующих функций, которые они получают вдоль координатных осей.

При составлении уравнений равновесия необходимо перейти от напряжений к силам, т.е. последовательно умножить напряжения, действующие по граням рассматриваемого элемента на величины их площадей, равных и . Если из объемных сил на грунт действует только собственный вес, то кроме сил, связанных с напряжениями, к элементу приложена сила его собственного веса, равная , где   удельный вес грунта.

Теперь запишем три уравнения равновесия плоской задачи  суммы проекций сил на координатные оси и уравнение моментов:

 X  0,  Z  0,  M  0.

(4.1)

Уравнение моментов  M  0 тождественно удовлетворяется в силу закона парности касательных напряжений _xz  _zx. Распишем первые два уравнения:

 X  0: ;  Z  0: .

(4.2)

После приведения подобных членов

,

и сокращения на общий множитель получим искомые уравнения равновесия

, .

(4.3)

В два полученных уравнения равновесия входят три неизвестные функции _x, _z, _xz координат x и z. Поскольку число неизвестных больше числа уравнений, то, очевидно, одних только уравнений равновесия недостаточно, чтобы однозначно определять поле напряжений в грунтовой среде. Для этого к ним необходимо присоединить еще уравнения, чтобы получить замкнутую систему уравнений.

Физическая сторона задачи. Напомним, что в общем случае пространственной задачи обобщенный закон Гука имеет вид (см. ф-лы (3.1) в п. 3.2.1):

; ; ; ; ; .

(4.4)

Напомним, что: E и   модуль деформации и коэффициент Пуассона, G  модуль сдвига, связанный с E и  соотношением

.

(4.5)

Из сказанного ранее о плоском деформированном состоянии можно сделать определенные выводы. Прежде всего, вследствие отсутствия внешних сил, действующих вдоль тела (вдоль оси Oу), в нем не могут возникать сдвиговые деформации в плоскостях хOу и yOz, т.е. в плоскостях, параллельных оси Oy. Поэтому имеет место равенство

,

(4.6)

из которого следует, что в любом поперечном сечении тела касательные напряжения отсутствуют. Таким свойством может обладать поперечное сечение, лежащее в плоскости симметрии. Следовательно, в бесконечно длинном теле при указанных условиях любое поперечное сечение совпадает с плоскостью симметрии. Но кроме указанного плоскость симметрии обладает еще одним важным свойством: при деформировании тела она остается неподвижной. Поэтому расстояние между любыми двумя поперечными плоскостями тела остается неизменным в процессе деформирования. В результате приходим к выводу о том, что относительная линейная деформация в направлении оси Oy также равна нулю:

.

(4.7)

Полученные равенства (4.6) и (4.7) показывают, что в рассматриваемых условиях деформации могут иметь место только в поперечных плоскостях. Это и послужило основанием для введения термина «плоская деформация».

Из равенства (4.7) имеем

.

(4.8)

Подставляя (4.8) в уравнения (4.4) и, учитывая (4.6), запишем обобщенный закон Гука для условий плоской деформации

; ; .

(4.9)

Теперь мы имеем дело с пятью уравнениями (4.3) и (4.9), содержащими шесть неизвестных функций координат  три компоненты напряжений и три компоненты деформаций.

Замыкать систему будут уравнения, связывающие перемещения точки грунта с ее деформациями, так называемая, геометрическая сторона задачи.

Геометрическая сторона задачи. Рассмотрим перемещения и деформации бесконечно малого элемента грунта ОАВС (рис. 4.6). Процесс деформирования и перемещения элемента, происходящий под действием прилагаемой к грунтовой среде нагрузки, условно разделим на два этапа. На первом этапе элемент переместится как жесткое тело из его начального положения ОАВС в положение О₁А₁В₁С₁. Перемещения точек вдоль осей Ox и Oz обозначим через u и w. На втором этапе имеем собственно деформирование элемента, которое состоит из деформаций изменения размеров и деформаций изменения формы. В результате элемент займет положение О₁А₂В₂С₂.

Рисунок 4.6.  Перемещения и деформации среды в точке

Определим деформации изменения размеров элемента, когда точки А₁, В₁ и С₁ переходят в положения А₂, В₂ и С₂. Следует помнить, что положительными в механике грунтов считаются деформации укорочения. Рассмотрим сначала величины горизонтальных перемещений для соседних точек О и А рассматриваемого элементарного объема грунта ОАВС вдоль оси Ox. Пусть точка О получила перемещение u, тогда перемещение точки А будет отличаться от u в меньшую сторону на величину частного дифференциала функции u  (x, z) вдоль оси Ox

,

т.е. длина грани О₁А₁ сократиться на величину .

Относительная деформация грани О₁А₁ по определению равна

,

(4.10)

Аналогичное рассмотрим вертикальные перемещения точек О и C. Перемещение точки О вдоль оси Oz составит w, а перемещение точки C

Тогда относительная деформация вдоль оси Oz составит

.

(4.11)

Теперь определим относительную деформацию сдвига, равную по определению

,

(4.12)

где ₁ и ₂  углы поворота граней O₁A₂ и O₁C₂.

Вследствие принятой гипотезы о малости деформаций углы ₁ и ₂ будут численно равны значениям своих тангенсов. Прежде, чем переходить к вычислению этих величин, найдем вертикальное перемещение точки A и горизонтальное точки C. В первом случае искомое перемещение будет отличаться от вертикального перемещения w точки O на частный дифференциал функции w  (x, z) вдоль оси Ox. Аналогично рассмотрев полное горизонтальное перемещение точки C, получим для него . Итак, запишем выражения для углов сдвига:

, .

(4.13)

В знаменателях формул (4.13) присутствуют по два слагаемых. Еще раз обращаясь к принятой гипотезе о малости деформаций, отбросим укорочения длин граней и как пренебрежимо малые величины по сравнению с их первоначальными размерами dx и dz.

Окончательно, учитывая (4.12) и (4.13) для сдвиговой деформации получим следующее выражение

.

(4.14)

Выражения (4.10), (4.11) и (4.14) иногда называют уравнениями Коши.

Исходные уравнения плоской задачи. Теперь имеем замкнутую систему из 8 уравнений (4.3), (4.9), (4.10), (4.11) и (4.14), содержащую 8 неизвестных функций координат x и z: напряжения  _x, _z, _xz, относительные деформации  _x, _z, _xz, перемещения точек грунта  u, w. Запишем ее окончательный вид:

статические уравнения

, ;

(4.15)

физические уравнения

, , ;

(4.16)

геометрические уравнения

, , .

(4.17)

4.2.4. Постановка пространственной задачи ТЛДС.

В целом постановка пространственной задачи ТЛДС вполне аналогична плоскому случаю. Поэтому здесь приведем лишь сводку определяющих уравнений в декартовой системе координат Oxyz (ось Oz направлена вертикально вниз, рис. 4.7) [2]:

Рисунок 4.7.  Схема напряженного состояния в точке (пространственная задача, декартовы координаты)

статические уравнения

, , ;

(4.18)

физические уравнения

, , , , , ;

(4.19)

геометрические уравнения

, , , , , .

(4.20)

Всего в общем случае пространственной задачи имеем 15 уравнений, содержащих 15 неизвестных функций координат x, y и z.

4.3. О решении задач теории линейно-деформируемой среды

4.3.1. Цель решения задачи

Цель решения любой задачи ТЛДС состоит в том, чтобы подобрать такие зависимости для всех искомых функций (напряжения, деформации и перемещения), которые бы тождественно удовлетворяли уравнениям (4.15)…(4.17) для плоского или (4.18)…(4.20) для пространственного случая, и при этом не противоречили граничным условиям. Последнее требование означает, что на границах основания получаемые напряжения должны находиться в равновесии с внешними нагрузками, а перемещения не должны противоречить условиям закрепления рассчитываемой области.

Методы строгих решений задач ТЛДС сложны и разнообразны, а их освещение в рамках данного учебника затруднено вследствие ограниченного объема. Кроме того, они получили достаточно широкое освещение в специальной литературе и учебниках по «Теории упругости» и некоторых монографиях по «Механике грунтов». Поэтому в этом параграфе будут даны лишь некоторые основные преобразования исходных уравнений к виду, более удобному для дальнейшего решения, а многие формулы в следующих параграфах будут даваться либо без выводов, либо с «адаптированными» выводами.

4.3.2. Определяющие уравнения. Уравнение совместности

Плоская задача в декартовой системе координат. Уравнение совместности. Исходная система уравнений плоской задачи в декартовых координатах, как было показано в предыдущем параграфе, включает восемь уравнений. Естественно попытаться ввести некоторые упрощения.

Прежде всего, исключим перемещения u и w из выражений (4.17). Продифференцируем первое из них дважды по z, второе дважды по x, третье сначала по x, потом по z:

, , .

Сравнивая полученные выражения, имеем

.

(4.21)

Это уравнение называется уравнением совместности или уравнением неразрывности деформаций. Физический смысл уравнения совместности заключается в том, что оно обеспечивает сохранение сплошности среды после деформирования.

Это уравнение следует объединить с уравнениями равновесия (4.15) в общую систему. Однако прежде надо преобразовать (4.21) к напряжениям. С этой целью подставим в него выражения закона Гука (4.16), предварительно взяв необходимые производные

, , .

В результате имеем

.

(4.22)

Найденное уравнение можно преобразовать к более компактной форме с помощью уравнений равновесия (4.14). С этой целью продифференцируем первое из уравнений (4.14) по x, а второе  по z и сложим:

.

Подставив это равенство в правую часть уравнения (4.22), после приведения подобных членов и сокращения на общий множитель (1  ) получим искомое уравнение совместности в прямоугольной системе координат, выраженное через напряжения:

.

(4.23)

Часто это уравнение записывают с помощью оператора Лапласа , тогда оно принимает более компактный вид:

.

(4.24)

Последнее равенство вместе с уравнениями равновесия составляют определяющую для плоской задачи систему из трех уравнений  два уравнения равновесия и уравнение совместности  с тремя неизвестными функциями напряжений, отыскание которых дает искомое решение плоской задачи:

, , .

(4.25)

Можно пойти дальше по пути упрощений. Введем некоторую функцию  (здесь   не угол внутреннего трения (!)), связанную с напряжениями следующим образом

, , .

(4.26)

Функция  называется функцией напряжений или функцией Эри. Нетрудно убедиться, что при подстановке выражений (4.26) в уравнения равновесия (4.15) получаются тождества. Функция напряжений, таким образом, позволяет свести определяющую систему плоской задачи (4.25) к одному уравнению:

,

(4.27)

или в компактной форме

.

(4.28)

В результате плоская задача определения напряженно-деформированного состояния грунтовой среды будет сводиться к решению только одного дифференциального уравнения, содержащего одну неизвестную функцию, которая должна удовлетворять этому уравнению и граничным условиям.

Плоская задача в полярной системе координат. Некоторые задачи удобно решать в полярной системе координат Or. В такой системе координат уравнения равновесия бесконечно малого элемента, показанного на рис. 4.8, имеют вид:

Рисунок 4.8.  Схема напряженного состояния в точке (плоская задача, полярные

координаты)

, .

(4.29)

Известно, что сумма нормальных напряжений по двум взаимно перпендикулярным площадкам  величина инвариантная, т.е. не зависящая от выбранной системы координат. Поэтому справедливы равенства

.

(4.30)

Используя эту величину, а также известные соотношения между декартовыми и полярными координатами , , уравнение совместности (4.23) или (4.24) можно преобразовать к полярной системе координат:

.

(4.31)

Окончательно определяющая система уравнений плоской задачи в полярных координатах r примет вид

, , .

(4.32)

Если пренебречь собственным весом среды ( ), можно ввести функцию напряжений посредством соотношений

, , .

(4.33)

Тогда уравнение совместности, аналогичное (4.27) и (4.28), запишется в виде

.

(4.34)

или

,

где .

Пространственная задача в декартовой системе координат. При решении пространственной задачи в напряжениях приходится сталкиваться с наиболее сложной ситуацией, на которой остановимся лишь коротко.

В рассматриваемом случае необходимо подобрать шесть функций для компонент напряжений, удовлетворяющих помимо уравнений равновесия (4.18) и граничных условий шести уравнениям совместности [2]

, , , , , ,

(4.35)

где , .

Осесимметричная задача в цилиндрической системе координат. Особый интерес представляет случай осевой симметрии. Схема осесимметричного напряженного состояния в точке в цилиндрической системе координат Orz показана на рис. 4.9 (ось Oz направлена вертикально вниз). Уравнения равновесия для этого случая имеют вид:

Рисунок 4.9.  Схема напряженного состояния в точке (осесимметричная задача,

цилиндрические координаты)

, .

(4.36)

Запишем уравнения совместности, опуская их вывод. При данном виде напряженного состояния таких уравнений четыре:

; ; ; ,

(4.37)

где .

Функции Эри, связанная с напряжениями равенствами

, ,

, ,

(4.38)

должна удовлетворять уравнению

,

(4.39)

или короче

,

где .

4.3.3. О методах решения задач теории линейно-деформируемой среды

Главная трудность при решении рассмотренных в п. 4.3.2 задач состоит в подборе такой функции напряжений, которая помимо уравнений (4.28), (4.34) или (4.39), удовлетворяла бы и граничным условиям. Можно задаться каким-либо определенным видом функции с некоторыми постоянными коэффициентами, исходя из физической сути задачи, граничных условий или других дополнительных соображений. Например, в известной в теории упругости задаче о силе, приложенной внутри упругого пространства функция Эри не должна содержать линейных размеров, поскольку их нет в самой задаче; в задаче о вертикальной силе, приложенной к полупространству (см. ниже задачу Буссинеска) ясно, что с глубиной напряжения должны уменьшаться и т.д.

Как только удается в конкретной задаче подобрать функцию Эри, то по соответствующим формулам нетрудно определить все компоненты напряжений, деформаций и перемещений в любой точке рассматриваемой области. Так, в плоской задаче для этого следует использовать зависимости (4.15)…(4.17).

В замкнутом виде получить эту функцию далеко не всегда возможно, и при решении приведенных выше уравнений широко используют метод конечных разностей. Если заменить частные производные в (4.28), (4.34) или (4.39) отношениями конечных приращений, то получим систему линейных алгебраических уравнений.

Другие подходы, также заключающиеся в применении численных решений, реализуются методом конечных элементов и методом граничных интегральных уравнений, которые получили значительное развитие в последние десятилетия. В МКЭ исследуемая область разбивается на отдельные конечные элементы, в пределах каждого из которых устанавливается связь между усилиями и перемещениями, а затем, используя вариационные принципы, для всех элементов составляется и решается общая алгебраическая система уравнений. В методе граничных интегральных уравнений искомые функции определены на границе области, и задача сводится к решению интегральных уравнений. Подробное описание методов аналитических и численных решений можно найти в специальной литературе.

Ниже мы будем останавливаться преимущественно на классических решениях базовых плоских и пространственных задач ТЛДС, полученных в замкнутом виде, и являющихся наиболее важными с практической точки зрения, результаты которых лежат в основе многих инженерных методов и расчетов.

4.3.4. Понятие о бытовых и дополнительных напряжениях

В инженерной практике при решении задач о напряженно-деформированном состоянии основания принято отдельно определять напряженное состояние, возникающее от собственного веса грунта и от внешних нагрузок. Такой подход вполне оправдан, поскольку в ТЛДС, как отмечалось, справедлив принцип суперпозиции. В соответствии со сказанным, введем понятия бытовых и дополнительных напряжений.

Бытовые напряжения  это напряжения, возникающие в основании от действия собственного веса грунта  веса вышележащих слоев. Обозначаются индексом «g», например, _zg.

Дополнительные напряжения  это напряжения, возникающие только от действия внешней нагрузки. Обозначаются индексом «p», например, _zp.

Полное напряженное состояние находится суммированием решений:

, ,

и т.д.

В дальнейшем при раздельном анализе бытового и дополнительного напряженного состояния индексы «g» и «p» будем, как правило, опускать.

Определение бытового напряженного состояния, вообще говоря, является крайне сложной задачей, поскольку для этого необходимо знать всю историю осадконакопления на территории каждой конкретной строительной площадки [30]. При этом может оказаться, что принцип линейной деформируемости будет вообще неприменим. Вместе с тем, на практике бытовые напряжения рассчитываются весьма просто вследствие обычно принимаемых дополнительных гипотез об упрощенном характере процесса осадконакопления (см. п. 4.4). Принято считать, что точности таких расчетов в большинстве случаев достаточно для инженерных целей. В результате основное внимание уделяют определению дополнительных напряжений, где особенно сложен поиск решений в замкнутом виде.

Итак, с точки зрения строгой постановки ТЛДС применение данной методики определения полных напряжений вполне корректно. Вместе с тем, этот прием используется и в приближенных расчетах. Например, учет неоднородности основания, который для бытового напряженного состояния в рамках обычно принимаемых допущений не представляет трудностей, при определении дополнительных напряжений выполняется сравнительно редко. Однако полученные в результате напряжения также суммируются, что для практических расчетов часто оказывается оправданным.

4.4 Задача о природном напряженном состоянии основания

Однородное основание. Рассмотрим простейший случай определения бытового напряженного состояния однородного изотропного линейно-деформируемого полупространства, ограниченного сверху горизонтальной плоскостью (рис. 4.10, а). Для большей общности положим, что на всей поверхности основания действует равномерно распределенное давление интенсивностью q. Возьмем прямоугольную систему координат, оси Oх и Oу которой расположены на поверхности основания, а ось Oz направим вертикально вниз. Поскольку в направлении осей Ox и Oy на поверхности основания ничего не изменяется, то, очевидно, напряжения в основании не зависят от координат х и у. В таком случае в дифференциальных уравнениях равновесия системы (4.15) частные производные и равны нулю. Более того, так как касательные силы на поверхности основания отсутствуют, то можно ожидать, что касательные напряжения _xz отсутствуют и внутри основания. Согласно сказанному, напряжения _x, _z могут зависеть только от одной координаты z. Поэтому частную производную в уравнении равновесия следует заменить на простую производную . В результате от двух уравнений равновесия остается одно простое уравнение

Рисунок 4.10.  Схемы к определению бытовых напряжений: (а) в однородном основании; (б) в слоистом основании

.

(4.40)

Интегрируя его, получим

,

(4.41)

где С  произвольная постоянная интегрирования.

Константу С определим из граничного условия на поверхности основания. Так как при z  0, _z  q, то С  q, и окончательно имеем

.

(4.42)

Таким образом, в однородном основании напряжение _z нарастает с глубиной по линейному закону (рис. 4.10, а).

Поскольку _xz  0, то напряжение _z является главным напряжением и, очевидно, наибольшим, так что _z  ₁. Помимо напряжения _z, для полноты картины надо отметить еще и боковые напряжения _x, _y. Эти напряжения установим, полагая, что деформации основания в процессе его геологического формирования происходили равномерно в направлении оси Oz, и в последующем оно не подвергалось тектоническим процессам (в других случаях определения бытовых напряжений также будем придерживаться этой гипотезы). При таких предположениях деформации основания под действием только собственного веса грунта происходили в условиях невозможности боковых деформаций _x  _y  0. Иначе говоря, деформирование совершилось в условиях компрессионного сжатия в направлении оси Oz. В таком случае боковые напряжения определяются зависимостями

,

(4.43)

где  коэффициент бокового давления в условиях компрессионного сжатия.

Ясно, что эти напряжения также являются главными, так что , а их эпюры качественно повторяют эпюру _z, но имеют меньшие в  раз ординаты.

Третье уравнение определяющей системы (4.25) очевидно удовлетворяется, так как вторые производные от по х и z равны нулю. Таким образом, полученное решение удовлетворяет всем уравнениям определяющей системы (4.25).

Отметим, что если отказаться от принятых допущений, то напряжения _х, _у окажутся неопределенными.

Основание с горизонтальным напластованием грунтов. Перейдем к случаю, когда в основании возможно выделить несколько инженерно-геологических элементов, залегающих горизонтально (рис. 4.10, б). Опустим выводы формул, они аналогичны только что рассмотренным. Большинство приведенных выше рассуждений также остается справедливым и в этом случае.

Запишем формулу для вертикального бытового напряжения, возникающего на глубине (рис. 4.10, б):

.

В общем случае для точки с координатой z, находящейся в n-м от поверхности слое эта формула примет вид:

,

В этих формулах: z  координата точки, в которой определяется напряжение, n  общее количество слоев, причем рассматриваемая точка находится в n-м слое; _i и h_i  удельный вес и мощность i-го слоя.

В произвольном i-м слое остальные напряжения определятся как

, ,

где  коэффициент бокового давления i-го слоя, _i коэффициент Пуассона i-го слоя.

Эпюра вертикальных напряжений _z дана на (рис. 4.10, б).

Однородное обводненное основание. Если основание обводнено (рис. 4.11, а), и вода свободно перемещается по порам грунта, то по закону Архимеда она оказывает взвешивающее действие на частицы грунта. Тогда для однородного обводненного основания напряжения на глубине z с учетом сказанного равны:

Рисунок 4.11.  Схемы к определению бытовых напряжений: (а) в однородном

обводненном основании; (б) в двухслойном обводненном основании

, , .

где  удельный вес грунта с учетом взвешивания водой, _s  удельный вес частиц грунта, _w  10 кН/м³  удельный вес воды, e  коэффициент пористости.

Степень взвешивания частиц грунта при его обводнении для разных видов грунтов будет различна [35]. Считается, что чем меньше общая площадь контактов между частицами, тем полнее проявляется взвешивание для каждой из них. Дело в том, что по площадям контактов между частицами гидростатическое давление воды не может передаваться. В этом случае имеет место, как говорят, неполное взвешивание частиц. Принято считать, что полному взвешиванию подвергаются пески и супеси, несколько хуже суглинки, а для плотных глин взвешивания может вообще не быть.

Двухслойное обводненное основание. Рассмотрим обводненное основание, например, в русле реки. Допустим, что с поверхности залегает водопроницаемый песчаный грунт, а подстилает его слой плотной глины (рис. 4.11, б). Этот слой можно считать водоупорным. Такая ситуация может встречаться в транспортном строительстве, в частности при сооружении мостовых переходов.

Итак, в песчаном слое в уровне его подошвы согласно вышесказанному вертикальные бытовые напряжения с учетом взвешивания водой составят

,

где  удельный вес песчаного грунта с учетом взвешивания водой, h  мощность его слоя.

Переходя в слой глины, очевидно, выталкивающая сила исчезает. Кроме того, глина будет воспринимать дополнительное давление от веса столба воды высотой H_w (рис. 4.11, б). Это давление компенсировалось в первом слое за счет всестороннего обжатия водой каждой частицы песка, т.е. гидростатического давления. В результате на границе слоев песка и глины в эпюре вертикальных напряжений возникает скачок, равный давлению от столба воды . Окончательно эпюра бытовых вертикальных напряжений примет такой вид, как показано на (рис. 4.11, б), а компоненты бытовых напряжений определятся зависимостями:

, , ,

где  удельный вес глины,   коэффициент бокового давления для соответствующего слоя.

4.5. Плоская задача определения напряжений от внешних нагрузок

4.5.1. Задача о погонной нагрузке (задача Фламана, 1892 г.)

Задача Фламана имеет фундаментальное значение, поскольку, как будет показано далее, оно позволяет решать разнообразные задачи о напряженно-деформированном состоянии основания в условиях плоской деформации.

Рассматриваемая задача состоит в следующем. Вдоль некоторой прямой, проведенной на поверхности основания, нормально к поверхности действует равномерно распределенная сосредоточенная погонная нагрузка p (рис. 4.12). Остальная часть поверхности основания остается свободной. Требуется определить напряженно-деформированное состояние основания от такой нагрузки. При этом в уравнениях равновесия надо полагать  = 0, поскольку будут определяться дополнительные напряжения.

Рисунок 4.12.  Напряженное состояние элемента основании в задаче Фламана

Переходя к решению задачи, предположим, что при указанных условиях загружения в основании возникает простое радиальное напряженное состояние, в котором _r  наибольшее главное напряжение ₁, а наименьшее главное напряжение _  0 и, следовательно, _r  0 (см. рис. 4.12). Принятое предположение будет оправдано в ходе решения. Сейчас же отметим, что оно удовлетворяет граничным условиям задачи, так как равенство _  0 означает отсутствие давления на поверхности основания, разумеется, за исключением точек оси Oу, где действует нагрузка p. Согласно этому предположению второе из уравнений системы (4.32) тождественно обращается в нуль, а первое уравнение принимает более простой вид:

.

Разделим в нем переменные

и проинтегрируем

,

где ()  произвольная функция угла  (напомним, что вместо произвольной постоянной при интегрировании уравнения в частных производных добавляется произвольная функция от аргумента, по которому не производилось интегрирование).

Отсюда

,

и после потенциирования получаем

.

(4.44)

Произвольная функция () должна удовлетворять третьему уравнению системы (4.32), т.е. уравнению совместности, и граничным условиям. Поскольку _  0, то согласно (4.30) . Теперь возьмем производные, входящие в уравнение совместности

, , .

и подставим их в это уравнение. В результате придем к уравнению

.

Известно, что общий интеграл этого уравнения имеет вид:

,

(4.45)

где C, C₁  произвольные постоянные.

При определении C, C₁ прежде всего необходимо учесть, что вертикальная координатная плоскость уОz является плоскостью симметрии напряженно-деформированного состояния основания. Это означает, что знак угла  не должен влиять на величину _r. Следовательно, функция () должна быть четной, т.е. должна удовлетворять условию () = (). Этому требованию удовлетворяет первое слагаемое в (4.45). Поэтому необходимо положить C₁ = 0, и выражение (4.44) принимает более определенный вид:

.

(4.46)

Остается определить константу C. С этой целью радиусом r вырежем из основания (рис. 4.13) полуцилиндр в направлении оси Oy длиной, равной единице. Под действием нагрузки p и напряжения _r он должен находиться в равновесии. В силу указанной симметрии необходимо удовлетворить только уравнению Z  0, остальные два уравнения X  0, Y  0 удовлетворяют автоматически.

Рисунок 4.13.  Схема к условию равновесия полуцилиндрического тела в задаче Фламана

Для составления уравнения Z  0 выделим на круглоцилиндрической поверхности полуцилиндра элементарную площадку шириной rd и длиной 1. Ее площадь d  1∙rd (см. рис. 4.13). На эту площадку действует элементарная сила

,

направленная по радиусу. Ее проекция на ось Oz равна , а с учетом выражения (4.46) будет . В сумме элементарные силы должны уравновешивать нагрузку p. Таким образом, уравнение равновесия  Z  0 полуцилиндра принимает вид:

.

Входящий сюда интеграл легко берется после подстановки равенства :

.

В результате находим значение произвольной постоянной

.

Подставив найденное значение С в (4.46), окончательно получим

.

(4.47)

Согласно формуле (4.47), линии _r  const представляют собой окружности, касающиеся поверхности основания в начале координат, как изображено на рис. 4.14. Действительно, для этого достаточно формулу (4.47) записать в виде

,

где  диаметр круга, касающегося поверхности в начале координат.

Рисунок 4.14.  Линии равных значений радиального напряжения в задаче Фламана

Задача определения напряженного состояния основания решена, поскольку определены главные напряжения ₁  _r и их направления. Однако для практического применения удобнее иметь дело с компонентами напряжения _x, _z, _xz. Необходимые преобразования можно выполнить с помощью известных формул

;

.

Полагая здесь ₁  _r; ₃  _  0 и учитывая, что главное напряжение в решаемой задаче составляет с осью Oz угол   , будем иметь

; .

Имея в виду равенства

, ,

и формулу (4.47) получим

, , .

(4.48)

Наконец, заменим здесь полярные координаты прямоугольными, используя зависимости между ними:

; ; .

В результате получим

, , .

(4.49)

Кроме этих напряжений, нормально к любой плоскости, параллельной плоскости хОz, действуют главные напряжения _y  ₂. Их величину можно определить из закона Гука для условия плоской деформации _y  0. Согласно (4.8)

.

Подставив сюда выражения для _x и _z из (4.49), получим

.

Найденные формулы для напряжений (4.47) и (4.49) можно получить, если задаться функцией напряжений в виде:

в полярной системе координат

,

в декартовой системе координат

.

Для того чтобы наглядно охарактеризовать напряженное состояние в задаче Фламана, на рис. 4.15 приведены эпюры напряжений _x, _z, _xz в двух горизонтальных сечениях, а также эпюра напряжения _z вдоль оси Oz. Эпюры _x, _z симметричны относительно оси Oz, причем первая имеет на оси Oz максимальное значение, а вторая равна нулю. Отметим еще, что все напряжения на любой прямой, проходящие через начало координат, уменьшаются в обратном отношении к расстоянию r и при обращаются в нуль, а при неограниченно растут. Например, вдоль вертикальной оси Oz x  0, тогда выражение (4.49) для _z примет вид

Рисунок 4.15.  Эпюры напряжений в основании в задаче Фламана

.

Взяв соответствующие пределы при , имеем

, .

На примере вывода формулы осадки в задаче Фламана покажем, как определяются деформации и перемещения, если известны напряжения.

Согласно закону Гука (4.16) и уравнениям Коши (4.17)

Отсюда после подстановки выражения для напряжений (4.49) и интегрирования получим

,

где (x)  произвольная функция x.

Входящие в это выражение интегралы можно найти в любой справочной таблице интегралов

,

.

После их подстановки будем иметь

.

Осадки точек поверхности основания получим, положив здесь , :

.

Предположим, что при имеем . Тогда

.

Подставив значение (x) в предыдущее выражение, окончательно получим

,

(4.50)

где C  произвольная постоянная в силу произвольности величины s.

Таким образом, в задаче Фламана осадку можно определить только с точностью до произвольного слагаемого.

График осадки поверхности основания показан на рис. 4.16. Видно, что в начале координат осадка бесконечно велика. Сосредоточенная погонная нагрузка как бы прорезает основание. Такой результат является следствием того, что напряжения с приближением к точке приложения силы теоретически возрастают до бесконечности, поскольку площадь опирания силы равна нулю. По закону Гука из этого следует, что и деформации здесь бесконечно велики, а вместе с ними, согласно зависимости Коши, бесконечно велики и перемещения. Вместе с тем необходимо помнить, что деформации должны быть достаточно малы.

Рисунок 4.16.  Осадка поверхности основания в задаче Фламана

4.5.2. Задача о произвольной полосовой нагрузке

Выделим на поверхности основания полосу постоянной ширины b  2a (рис. 4.17) и бесконечной длины. К ней приложим давление, изменяющееся поперек полосы по некоторому закону p  p(). Вдоль полосы давление не меняется. Ставится задача  определить напряженно-деформированное состояние основания от такой нагрузки.

Рисунок 4.17.  Схема к определению напряжений в основании от полосовой нагрузки, распределенной по произвольному закону

Возьмем в основании произвольную точку M с координатами x, z, а на полосе загружения на расстоянии  от начала координат выделим бесконечно узкую полоску шириной d. Приложенное к полоске давление заменим бесконечно малой сосредоточенной силой dP  p()d. Расстояние от точки приложения этой силы до точки M определяется координатой z и разностью x  . Используя формулы Фламана (4.49), можно определить бесконечно малые величины напряжений в точке М от силы dP. Для этого достаточно в формулах (4.49) заменить нагрузку p на p()d, а координату x на x  :

, , .

(4.51)

Напряжения в точке M, очевидно, получим, проинтегрировав эти выражения по всей ширине полосы загружения:

, , .

(4.52)

На этом, собственно, можно и закончить определение напряженного состояния основания от полосовых нагрузок, поскольку дальше следует чисто математическая операция взятия записанных интегралов. Сложность этой операции зависит от сложности закона распределения давления p(). В аналитическом виде решения получены, в частности, для равномерного давления const (см. следующий пункт), для треугольного закона распределения давления поперек полосы. Суперпозиция этих двух решений дает выражение для трапецеидального закона давления. Получены решения и для некоторых других законов распределения давления. Но даже если закон p() настолько сложен, что интегралы в (4.52) не берутся, их всегда можно вычислить приближенно, заменив интегрирование суммированием.

4.5.3. Задача о равномерной полосовой нагрузке (задача Мичелла,

1902 г.)

Эта задача является наиболее важной в практическом отношении, поскольку считается, что длинный, так называемый ленточный фундамент, центрально загруженный сосредоточенной силой, создает равномерное полосовое давление на основание. В этом же случае наиболее просто выполняется интегрирование в формулах (4.52). Однако предпочтительнее получить решение в переменных r, , используя в качестве исходных формулы задачи Фламана (4.48). Полученные при этом формулы имеют более компактный вид.

На полосе загружения выделим элементарную полоску шириной dx и из произвольной точки основания М (рис. 4.18) проведем в края этой полоски лучи. Из элементарного прямоугольника треугольника ABC имеем . Приложенное к полоске давление p₀ заменим элементарной сосредоточенной силой . Используя формулы (4.48), определим бесконечно малые значения напряжений в точке М:

Рисунок 4.18.  Схема к определению напряжений в основании от равномерной полосовой нагрузки

, , .

Отсюда

, , .

В результате интегрирования имеем

; ; .

(4.53)

Эти формулы можно преобразовать к более компактному виду, если ввести углы ,  с помощью равенств

, , , .

(4.54)

Подставляя пределы интегрирования в (4.53) и заменяя углы ₁ и ₂ на  и , имеем

;

;

теперь формулы (4.53) могут быть переписаны так:

; .

(4.55)

В соответствии с этими формулами показано распределение компонент напряжений в двух вертикальных и горизонтальных сечениях в основании (рис. 4.19).

Рисунок 4.19.  Эпюры напряжений _z в основании от равномерной полосовой нагрузки

интенсивностью p₀

С помощью этих формул и формул преобразования напряжений

определим главные напряжения

.

Окончательно имеем

.

(4.56)

Отметим, что угол   это угол, при котором видна полоса загружения из точки М (см. рис. 4.18). Поэтому он получил название угол видимости.

Далее можно показать, что наибольшее главное напряжение ₁ направлено по биссектрисе угла видимости. Действительно, угол  между осью Oz и направлением ₁ определяется формулой

.

Подставляя сюда выражение (4.55), получим

.

Отсюда с учетом второго из равенств (4.54)

.

Полученное равенство доказывает, что линия действия главного напряжения ₁ проходит по биссектрисе угла видимости.

С помощью формул (4.56) можно проанализировать распределение главных компонент напряжений в основании. В качестве примера на рис. 4.20 показано распределение главных компонент напряжений и отношения .

Рисунок 4.20.  Линия равных значений главных напряжений в основании от равномерной полосовой нагрузки

Кроме приведенных напряжений нормально к любой плоскости, параллельной плоскости xOz, согласно формуле (4.8) действуют напряжения

.

На сегодняшний день, учитывая доступность персональных ЭВМ, удобно использовать формулы для компонент напряжений в декартовой системе координат

,

.

Осадку поверхности основания в рассматриваемой задаче проще всего определить с помощью формулы осадки в задаче Фламана (4.50). Для этого с помощью формулы (4.50) запишем бесконечно малую осадку в некоторой точке поверхности с координатой x от бесконечно малой силы p₀d, расположенной в пределах полосы загружения на расстоянии  от начала координат:

.

При интегрировании этого выражения следует отдельно рассмотреть случай и случай .

Объединяя эти два результата для точек поверхности основания, расположенных справа от начала координат, с точностью до произвольного слагаемого, можем записать

, .

(4.57)

Верхние знаки здесь относятся к точкам интервала , а нижние  точкам интервала . График правой половины симметричной относительно начала координат эпюры осадки показан на рис. 4.21.

Рисунок 4.21.  Эпюры осадки поверхности основания от полосовой равномерной нагрузки

4.5.4. Задача о треугольной полосовой нагрузке

Эта задача имеет значение для строителей железных и автомобильных дорог, поскольку может использоваться при определении напряжений в основаниях насыпей. Если разбить трапецеидальную нагрузку от насыпи на основание на три  равномерно распределенную интенсивностью p и две симметричные треугольные, то, применяя принцип суперпозиции, в каждой точке основания можно отдельно определять напряжения от каждой из трех составляющих общей нагрузки, а затем их складывать.

Напряжения от равномерной нагрузки интенсивностью p нами рассмотрены выше (п. 4.5.3). Напряжения в точке M (x, z), возникающие в основании от действия одиночной треугольной полосовой нагрузки (рис. 4.22), могут быть найдены по формулам (Польшин, 1933):

,

, (4.58)

.

Рисунок 4.22.  Схема к определению напряжений в основании от треугольной

полосовой нагрузки

Вертикальное перемещение точек поверхности в случае действия одиночной треугольной нагрузки составит:

. (4.59)

4.5.5. Задача о погонных нагрузках, приложенных на некоторой глубине внутри основания (задача Мелана, 1932)

В заключение параграфа о плоских задачах определения дополнительных напряжений в линейно-деформируемом основании, ограниченном горизонтальной плоскостью, приведем два наиболее общих решения. Оба решения были даны Е. Меланом в 1932 г., а затем уточнены М.И. Горбуновым-Посадовым в 1954 г.

Пусть на некоторой глубине d действует вертикальная погонная нагрузка интенсивностью p (рис. 4.23). В этом случае функция напряжений имеет вид:

Рисунок 4.23.  Схема к определению напряжений в основании в задаче Мелана

для вертикальной погонной нагрузки

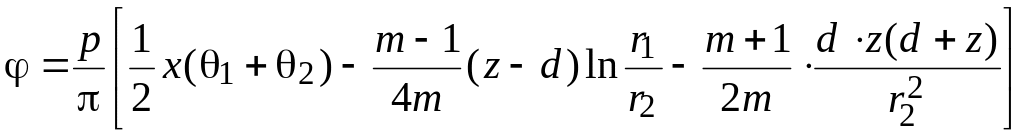(4.60)

Тогда компоненты напряжений определятся следующими зависимостями:

(4.61)

(4.62)

(4.63)

Нетрудно убедиться, что при и представленные зависимости совпадают с решением Фламана.

Запишем далее выражения для перемещений

(4.64)

где , .

Предположим теперь, что некоторой глубине d действует горизонтальная погонная нагрузка интенсивностью q, направленная как показано на рис. 4.24. В этом случае функция напряжений имеет вид:

Рисунок 4.24.  Схема к определению напряжений в основании в задаче Мелана

для горизонтальной погонной нагрузки

. (4.65)

Напряжения и перемещения точек среды равны

(4.66)

(4.67)

(4.68)

(4.69)

Используя приведенные зависимости и применяя принцип суперпозиции, можно получить выражения для напряжений, возникающих от действия как угодно сориентированной нагрузки, действующей на любой глубине или на поверхности, а затем, интегрируя, перейти от погонных нагрузок к полосовым. Таким образом, несмотря на громоздкость выражений (4.60)…(4.69), они могут быть полезны в практических расчетах для решения с помощью ЭВМ самых разнообразных задач о нагружении горизонтального изотропного однородного линейно-деформируемого основания.

4.6 Пространственная задача определения напряжений от внешних нагрузок

4.6.1. Задача о сосредоточенной силе (задача Буссинеска, 1885 г.)

Рассмотрим действие сосредоточенной вертикальной силы на поверхность полупространства. Эта задача считается основной в теории напряженного состояния оснований. Решение ее было получено Ж. Буссинеском в 1885 г.

На рис. 4.25 показана расчетная схема задачи в декартовой системе координат Oxyz: плоскость Oxy совпадает с горизонтальной поверхностью пространства, ось Oz вертикальна. Сосредоточенная вертикальная сила приложена в начале координат. Определим величину вертикальных сжимающих напряжений от этой силы.

Для произвольной точки М в основании обозначим радиусом r расстояние от начала координат, угол между радиусом r и осью Oz обозначим параметром , угол между осью Ox и проекцией радиуса на плоскость Оху  параметром . В окрестности точки М выделим элементарный объем, ограниченный двумя элементами шаровых поверхностей dA₁, dA₂ с радиусами r и и плоскими гранями, положение которых определяется углами d и d (см. рис. 4.25). На площадке dA₁ действует радиальное напряжение _r, на площадке dA₂  напряжение . Элементарные площади dA₁ и dA₂, пренебрегая малыми высших порядков, равны:

Рисунок 4.25.  К задаче Буссинеска

, .

Из уравнения равновесия выделенного элементарного объема имеем:

, ,

,

,

Пренебрегая величиной большего порядка малости , получим

.

Интегрируя это уравнение, приходим к выражению

, .

Функция () должна удовлетворять следующим условиям: ()  () в силу симметрии, согласно граничным условиям. Примем функцию (B = const), отвечающую указанным равенствам. Для нахождения константы B рассмотрим в основании полусферическую поверхность радиусом r (рис. 4.25). По этой полусфере будут действовать радиальные напряжения:

.

Составим уравнение равновесия всех сил на ось Oz для выделенной части основания:

.

(4.70)

Из этого уравнения найдем константу B:

.

Соответственно радиальные напряжения определятся формулой

.

Поскольку на сферической поверхности отсутствуют касательные напряжения, вертикальные напряжения можно найти по формуле

.

Переходя к декартовой системе координат, запишем выражение для _z, в виде

,

где .

Приведем выражения для всех компонент напряжений в декартовой системе координат:

; ; ; ; ; .

(4.71)

Для перемещений параллельно осям координат даются формулы:

; ; .

(4.72)

Выражения для компонент деформаций нетрудно получить, подставляя (4.71) в обобщенный закон Гука (4.19).

Полученные зависимости также можно получить, если принять функцию напряжений в виде (в цилиндрических координатах Orz):

, , , .

Наглядное представление об изменении напряжений в основании можно получить из рис. 4.15, где показаны эпюры вертикальных, горизонтальных нормальных и касательных напряжений в плоской задаче Фламана. Отличие в случае пространственной задачи Буссинеска заключается в том, что с глубиной уменьшение или рассеивание напряжений происходит быстрее, чем в плоской задаче.

4.6.2. Задача о произвольном нормальном давлении

Для определения напряжений и перемещений в основании при действии на его поверхности произвольной нормальной нагрузки используется решение Буссинеска о сосредоточенной силе и принцип суперпозиции.

На рис. 4.26 в декартовой системе координат изображена произвольная площадка A, на которую действует произвольное нормальное давление p(, ), ,   координаты нагрузки вдоль осей Ox и Oy. Выделив элементарную площадку , приложим к ней элементарную сосредоточенную силу . Тогда в произвольной точке M с координатами x, y, z по формулам (4.71) можно найти бесконечно малые величины напряжений и перемещений от силы dP. Проинтегрировав полученные выражения по площади загружения A, найдем искомые напряжения и перемещения в точке M от заданной нагрузки. Например, для вертикального напряжения _z справедливо выражение

;

(4.73)

где A указывает на действие интегрирования в пределах всей загруженной площадки.

Аналогичные выражения можно записать и для остальных компонент напряжений и перемещений.

Рисунок 4.26.  Расчетная схема загруженной площадки произвольной формы

4.6.3. Задача о равномерном давлении (задача ЛяваКороткина 1929, 1938). Формула Шлейхера

Решение задачи о равномерно нагруженной прямоугольной площадке наиболее часто используется в практических расчетах. А. Лявом в 1929 г. были получены выражения для сжимающих напряжений _z, а впоследствии В.Г. Короткин (1938 г.) получил формулы для всех компонент напряжений. Поэтому рассматриваемое решение называют задачей Лява-Короткина.

Приведем некоторые результаты упомянутых решений. На рис. 4.27 показана прямоугольная площадка размером , загруженная нормальным давлением интенсивностью p. Обозначим  меньший размер загруженной площади. Центр декартовой системы координат помещен в угол площадки, а оси Ox и Oy сориентированы по ее сторонам. Рассмотрим точку M на оси Oz, расположенную на глубине z под углом загруженного прямоугольника. Пользуясь приемом, изложенным в предыдущем параграфе, в соответствии с формулой (4.73) и обозначениями на рис. 4.27 запишем выражение для вертикального напряжения в точке M:

.

(4.74)

Введем обозначения , и запишем результат интегрирования выражения (4.74) в виде

  .

(4.75)

Рисунок 4.27.  Расчетная схема задачи Лява-Короткина

Выражение, обозначенное , называется коэффициентом рассеивания напряжений и зависит, как видно из формулы (4.75), от соотношения сторон загруженного прямоугольника n и относительной глубины расположения рассматриваемой точки m. Индекс «угл» показывает, что данное выражение справедливо для точек, расположенных под углом загруженной площадки.

Приведем еще две формы записи выражений для вертикальных напряжений в точках, находящихся либо под краем (углом) загруженной площади, либо под ее центром

;
,	(4.76)

где  полуширина загруженной площади, l  половина ее длины.

Из выражений (4.76) следует, что напряжения в точке, находящейся под центром площади на глубине z  h в 4 раза больше, чем в точке, находящейся под краем площади на глубине z  2h, т.е.

,

(4.77)

Пользуясь выражением для вертикального перемещения задачи Буссинеска (4.72), запишем формулу для величины w в точках под углом загруженного прямоугольника:

  ,

(4.78)

Коэффициенты A и B, как и коэффициенты рассеивания напряжений, зависят только от соотношений n и m. В рассматриваемом случае они равны

;

.

При различной в плане площади нагружения в выражении (4.78) коэффициенты A и B, очевидно, будут определяться иначе или вообще могут представлять собой неберущиеся интегралы.

Применяя принцип суперпозиции выражение (4.78) можно переписать для точки, находящейся под центром загруженной площади

,

(4.79)

где   коэффициент формы, зависящий от формы площади нагружения.

Выражение (4.79) называется формулой Шлейхера и имеет самостоятельное практическое значение. Согласно действующим нормам его используют для расчета модуля деформации грунта в штамповых испытаниях (см. п. 3.8.2). Кроме этого, его можно применять для определения осадок однородного основания.

4.6.4. Метод угловых точек

Формулы (4.75)…(4.76) для расчета напряжения _z под углом загруженной равномерным давлением прямоугольной площадки с помощью принципа суперпозиции позволяет определить вертикальное напряжение _z в любой точке основания. Для этого составляется ряд условных прямоугольных загруженных площадок, для каждой из которых рассматриваемая точка находится под углом. В сумме загруженные площадки должны давать исходную нагрузку. Такой прием определения _z называют методом угловых точек. Используя метод угловых точек, можно найти напряжения в основании от загруженных равномерным давлением площадок различных очертаний, которые можно составить суммированием ряда прямоугольников.

Рассмотрим несколько примеров. На рис. 4.28, а, б, в показан ряд загруженных площадок и положение в плане точки M. Напряжение _z для приведенных случаев можно рассчитать по формулам:

Рисунок 4.28.  К методу угловых точек

Цифры у коэффициентов  показывают прямоугольники, для которых определяется  (индекс «угл» опущен).

Нетрудно заметить, что для точек, лежащих под центром загруженной площадки, будет справедливо выражение (4.77), уже записанное нами ранее,

.

(4.80)

Для облегчения практических расчетов составлены специальные таблицы значений коэффициентов рассеивания напряжений _угл и _центр. Иначе эти коэффициенты можно найти из формул (4.76).

Метод угловых точек можно распространить и для определения вертикальных перемещений любой точки основания. Тогда нужно выполнять аналогичные операции с коэффициентами A и B из формулы (4.78).

4.6.5. Задача о сосредоточенных силах, приложенных на некоторой глубине внутри основания (задача Миндлина, 1936 г.)

Здесь приведем задачу о вертикальной и горизонтальной сосредоточенных силах, приложенных внутри основания на некоторой глубине. Аналогичные решение уже были нами рассмотрены в плоской постановке в п. 4.5.5. Расчетная схема задачи о вертикальной силе дана на рис. 4.29., а о горизонтальной силе в декартовых координатной системе  на рис. 4.30. Эти задачи были решены Миндлиным в 1936 г.

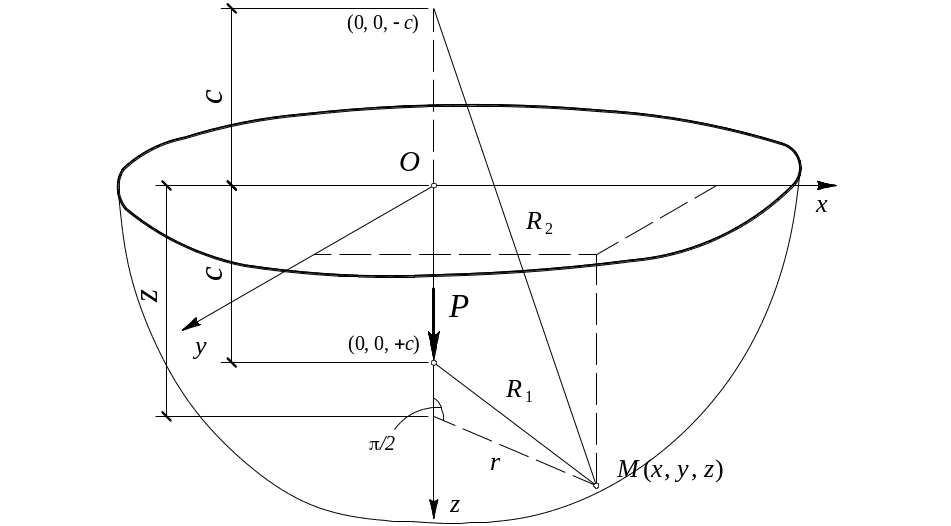
Рисунок 4.29.  Схема к определению напряжений в основании в задаче Миндлина

для вертикальной сосредоточенной силы

Приведем выражения для компонент напряжений и перемещений.

Случай вертикальной силы (рис. 4.29).

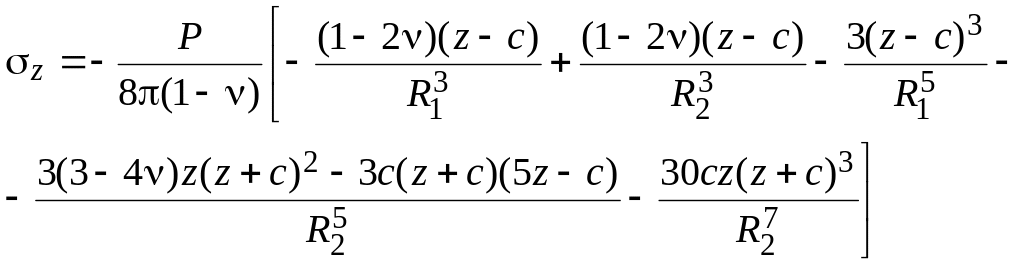(4.81)

(4.82)

Случай горизонтальной силы (рис. 4.30).

Рисунок 4.30.  Схема к определению напряжений в основании в задаче Миндлина

для горизонтальной сосредоточенной силы

(4.83)

(4.84)

.

4.7. Практические методы расчета осадок оснований

Определение осадок методом послойного суммирования

В предыдущих разделах мы не раз обращались к величинам перемещений и осадок основания. Однако во всех случаях грунт предполагался однородным, что в реальных условиях встречается редко. В этом пункте приводится более универсальный метод расчета осадок линейно-деформируемого полупространства, который называется метод послойного суммирования. Метод послойного суммирования является приближенным, но, вместе с тем, он очень широко используется в практике проектирования при расчете деформаций оснований фундаментов. в этом методе приняты некоторые упрощения, например, при определении бытовых напряжений неоднородность основания учитывается, а при определении дополнительных  нет. Возможность бокового расширения грунта учитывается интегральным коэффициентом 0,8.

На рис. 4.31 показана расчетная схема основания и фундамента. Фундамент шириной b передает на основание давление p₀, приложенное в уровне подошвы фундамента FL. Действие грунта, расположенного выше подошвы фундамента, заменяется эквивалентной пригрузкой , где d  глубина заложения фундамента от природного уровня рельефа NL. Построим координатную ось Oz, как показано на рис. 4.31. Деформации основания будут определяться для точек под центром фундамента.

Рисунок 4.31.  Схема к расчету осадок методом послойного суммирования

Приведем последовательность расчета.

1. Ниже подошвы фундамента основание разбивается на условные слои толщиной . При этом надо следить, чтобы границы условных слоев совпадали с границами реальных инженерно-геологических элементов. Заметим, что количество слоев пока не известно.

2. Определяем ту часть внешней нагрузки, действие которой будет вызывать деформирование грунта:

,

где  природное напряжение в уровне подошвы фундамента.

Это следует из принятой гипотезы: деформация основания не начинается до тех пор, пока внешняя нагрузка не превысит вес грунта, вынутый при разработке котлована.

3. Определяем бытовые напряжения в каждом i-ом слое с учетом природного напряжения в уровне подошвы

.

Здесь  координата центра тяжести i-ого слоя  удельный вес грунта, в котором находится i-ый слой. В результате строим эпюру бытовых напряжений, на рис. 4.31 она дана слева от оси Oz.

4. Определяем дополнительные напряжения в каждом i-ом слое, которые согласно решению ЛяваКороткина равны

,

где  коэффициент рассеивания напряжений, определяемый согласно из (4.76), 2l  длина фундамента.

5. Определяем мощность активной зоны сжатия. Понятно, что с глубиной вклад в общее напряженное состояние дополнительных напряжений по сравнению с бытовыми становится пренебрежимо мал (см. рис. 4.31). Поэтому осадку, рассчитываемую как раз от дополнительных напряжений, имеет смысл определять только в верхних слоях основания, где величина дополнительных напряжений существенна. Назначение такой глубины выполняют, исходя из эмпирических данных (Морозов, 1938). Считается, что для большинства грунтов рассмотрение напряженно-деформированного состояния основания не существенно, начиная с глубины, на которой выполняется условие

.

Расстояние от подошвы фундамента до указанной глубины называют мощностью активной зоны сжатия H_c, в пределах которой и вычисляют осадку.

6. В пределах указанной глубины  активной зоны сжатия  рассчитываем осадку каждого i-ого слоя грунта:

,

где E_i  модуль деформации грунта, в котором находится i-ый слой,   коэффициент, учитывающий ограниченную возможность бокового расширения грунта аналогично коэффициенту , рассмотренному в главе о компрессии, обычно принимают   0,8.

Заметим, что отношение есть относительная деформация i-го слоя, а представленное выражение  закон Гука.

7. Окончательно осадка определится по формуле:

,

где H_с под знаком суммы означает, что суммирование ведется в пределах активной зоны сжатия.

Представленная методика, таким образом, позволяет, хотя и приближенно, учитывать напластование грунтов с различной деформируемостью. Кроме того, используя метод угловых точек можно определять осадку в произвольной точке основания, а не только под центром и под краем, или легко учесть влияния соседних сооружений.

Особо следует подчеркнуть, что этот расчет можно выполнять, только если внешнее давление не превышает первой критической нагрузки и грунт работает в первой фазе деформирования по Н.М. Герсеванову  фазе уплотнения.

Расчетная схема линейно-деформируемого слоя конечной толщины.

Расчетная схема линейно-деформируемого слоя конечной толщины распространяется на случаи, когда в основании на некоторой глубине расположен практически несжимаемый грунт, например, скальная порода. Эту схему называют основанием с жестким подстилающим слоем. Расчет осадок такого основания производится преимущественно с использованием решений К.Е. Егорова.

Жесткий подстилающий слой приводит к изменению распределения сжимающих напряжений по глубине, а именно к концентрации напряжений, к более медленному их затуханию. Этот эффект тем больше, чем тоньше сжимаемый слой грунта. Поэтому влияние жесткого подстилающего слоя будет зависеть от отношения , где H  толщина сжимаемого слоя (или глубина расположения жесткого подстилающего слоя, a  полуширина прямоугольной или радиус круглой загруженной площади).

Приступая к определению осадки, вначале рассмотрим разность s вертикальных перемещений точек, лежащих на одной вертикали, но на различной глубине, определенную по теории линейно-деформируемого полупространства:

.

Выражение для w(z) можно представить в виде:

.

Величина зависит от формы загруженной площади, условий передачи нагрузки на основание и расположения вертикали, по которой находятся перемещения. Например, в частном случае, прямоугольной площади, загруженной равномерной вертикальной нагрузкой, величина для точек основания под ее углом определяется выражением в квадратных скобках в формуле (4.28):

Таким образом, выражение для осадки s (в данном случае разности вертикальных перемещений точек на глубинах z₁ и z₂) можно записать в виде:

Для осадок поверхности , относительно перемещения на некоторой глубине H , будем иметь:

Очевидно, что при расположении на глубине H несжимаемого грунта приведенная формула дает искомую абсолютную осадку поверхности основания. Если в пределах сжимаемой толщи H расположены грунты с различной сжимаемостью, характеризуемой параметрами деформируемости: E  модуль деформации и   коэффициент Пуассона, то осадку этой толщи можно определить выражением:

В последнем выражении n  это число слоев с различными параметрами деформируемости, расположенные в пределах сжимаемой толщи мощностью H и имеющие кровлю на глубине z_i1 и подошву на глубине z_i.

Теперь перейдем к учету жесткого подстилающего слоя. Эффект концентрации напряжений, вызываемый его наличием, можно приближенно учесть с помощью коэффициента влияния M, введенного К.Е. Егоровым:

Значения коэффициента M приведены в таблице в зависимости от отношения глубины расположения жесткого подстилающего слоя .

Значения коэффициента M влияния жесткого подстилающего слоя

	0…0,5	0,5…1	1…2	2…3	3…5	>5
M	1,5	1,4	1,3	1,2	1,1	1,0

Данные приведенной таблицы наглядно показывают степень влияния жесткого подстилающего слоя в зависимости от глубины его залегания. Расчетная схема линейно-деформируемого слоя конечной толщины нашла широкое применение, например, для расчета осадок плитных фундаментов, ширина которых более 10 м.

4.8 Контактная задача

С точки зрения реальной работы оснований фундаментов граничные условия в ряде рассмотренных решений имеют один существенный недостаток, в частности, в решениях Мичелла и ЛяваКороткина. Он заключается в том, что, прикладывая нагрузку к основанию, мы получали криволинейное очертание поверхности в месте приложения нагрузки (рис. 4.32, а). Следовательно фундамент в этих решениях не только получал осадку, а изгибался, причем изгиб полностью определялся деформацией основания, а в качестве осадки принимался максимальный «прогиб» линии подошвы фундамента.

Рисунок 4.32.  Схемы абсолютно жесткого, абсолютно гибкого и конечной

жесткости фундаментов

Реальные же фундаменты почти всегда имеют жесткость много выше жесткости основания, сложенного дисперсными грунтами. Это означает, что деформированный вид системы «основание-фундамент» будет ближе к показанному на рис. 4.32, б, в.

Таким образом, можно выделить три типа фундаментов:

• абсолютно гибкий фундамент, когда деформированный вид линии подошвы фундамента следует за деформациями основания, т.е. нагрузка как бы состоит из отдельных несвязанных между собой элементарных сил (рис. 4.32, а);

• абсолютно жесткий фундамент, когда линия подошвы остается прямой после деформации (рис. 4.32, б);

• фундамент конечной жесткости, когда линия подошвы деформируется, но величина деформации определяется соотношением конечных жесткостей основания и фундамента (рис. 4.32, в).

Различие в деформированных схемах, несомненно, повлечет за собой и несовпадение напряженного состояния, особенно в местах приложения давления. В этой связи важно отметить следующее.

Согласно принципу Сен-Венана по мере удаления от места приложения нагрузки напряженное состояние все меньше зависит от способа передачи нагрузки на среду и определяется лишь величиной нагрузки. Поэтому приходим к важному выводу о корректности рассмотренных выше решений ТЛДС для задач определения напряженно-деформированного состояния основания в целом. Однако также очевидно, что в некоторой области основания, непосредственно примыкающей к загруженной границе, расхождения с реальной картиной напряженно-деформированного состояния основания будут уже существенными.

Указанная проблема обычно рассматривается в контактных задачах. Под контактной задачей понимают задачу определения давлений на границе контакта между двумя телами. В данном случае одним телом является фундамент, другим  грунтовое основание.

Знание контактных давлений необходимо при расчете фундамента на прочность и определении напряженно-деформированного состояния основания.

Рассмотрим вначале модель фундамента, а затем модели основания.

В постановке классической контактной задачи принимаются следующие гипотезы:

• для фундаментов применима гипотеза плоских сечений;

• внешнее воздействие на фундамент полностью уравновешивается реакцией грунта по подошве;

• грунт и фундамент деформируются совместно, т.е. отсутствует «отлипание» фундамента от основания;

• в рассматриваемых ниже решениях трением по подошве пренебрегаем, т.е. подошвы фундаментов считаем абсолютно гладкими.

Первая из данных гипотез обеспечивает правомерность применения уравнения изогнутой оси балки. Из курса Сопротивления материалов известно, что для балки в сечении с координатой x прогиб w(x), угол поворота сечения (x), изгибающий момент M(x), перерезывающая сила Q(x) и распределенная нагрузка q(x), действующая на балку, связаны следующими дифференциальными соотношениями:

, (4.85)

где EI  постоянная по длине жесткость балки.

Вообще говоря, в рассматриваемой задаче мы имеем дело не с балкой, а с некоторой загруженной фундаментной лентой (полосой), работающей в условиях плоской деформации. Для такой полосы уравнения (4.85) также являются справедливыми с тем отличием, что вместо изгибной жесткости EI балки будем иметь цилиндрическую жесткость полосы фундамента:

, (4.86)

где E_F и _F  модуль упругости и коэффициент Пуассона материла фундамента, I_F  момент инерции поперечного сечения полосы фундамента.

Для случая, показанного на рис. 4.33, давление q(x) определится как

, (4.87)

где f(x)  внешняя нагрузка на полосу, как правило, заданная, p(x)  реакция по подошве полосы, как правило, искомая.

Рисунок 4.33.  Схема нагрузок на фундаментную полосу на основании

Тогда, с учетом (4.85)…(4.87) окончательно имеем

. (4.88)

В одно дифференциальное уравнение (4.88) входят две неизвестные функции w(x) и p(x). Следовательно, для получения решения необходимо записать дополнительные уравнения, связывающие осадку основания w(x) на границе контакта и искомую реакцию p(x).

Для описания работы основания используют две основные модели [10]  модель основания ФуссаВинклера (1801, 1867) и модель линейно-деформируемой среды.

Наглядно принципиальное отличие этих моделей продемонстрировано на рис. 4.34. Основное их отличие состоит в следующем. В модели линейно-деформируемой среды грунт деформируется не только в месте приложения нагрузки, но и на значительном расстоянии от нее (рис. 4.34, а). В модели ФуссаВинклера деформация предполагается только в местах приложения нагрузки (рис. 4.34, б). Считается, что первый случай лучше отвечает более прочным грунтам  песчаным и твердым глинистым грунтам, а второй более слабым  водонасыщенным глинистым.

Рисунок 4.34.  Схема линейно-деформируемого основания (а) и основания

ФуссаВинклера (б)

Подробней особенности данных моделей и вытекающие из них следствия рассмотрим далее.

4.8.1. Модель основания ФуссаВинклера

В основу данной модели положена следующая дополнительная гипотеза: грунт деформируется только в местах приложения нагрузки, причем в каждой точке осадка прямо пропорциональна величине давления (рис. 4.34, б):

, (4.89)

где k  коэффициент постели  величина, характеризующая деформационные свойства основания.

Эта гипотеза называется гипотезой коэффициента постели. Из (4.89) следует, что коэффициент постели численно равен давлению, вызывающему единичную осадку. Формула (4.89) дана для участка единичной длины в направлении оси Oy, как и ранее в случаях плоской деформации.

Подставляя (4.89) в уравнение изогнутой оси (4.88), имеем

, (4.90)

или

, (4.91)

где

.

Опуская вывод, сразу запишем интеграл данного уравнения, который обычно дается в виде:

,

или

. (4.92)

Здесь: A₁, A₂, A₃, A₄  постоянные интегрирования, получаемые из граничных условий, Y₁, Y₂, Y₃, Y₄  функции А.Н. Крылова, равные

, ,

, ,

где и  гиперболические синус и косинус.

Приведем простое решение для частного случая, когда фундамент можно принять абсолютно жестким (рис. 4.35). Поскольку абсолютно жесткий фундамент не деформируется, то подошва после приложения нагрузки также остается прямой, и уравнение линии подошвы фундамента можно представить в виде:

Рисунок 4.35.  Напряжение по подошве абсолютно жесткого фундамента

на основании ФуссаВинклера

,

где w₀  осадка основания в точке x  0,   угол наклона подошвы к горизонту.

Согласно (4.89) напряжения по подошве равны

.

Полученную трапецеидальную эпюру напряжений можно представить в виде суммы эпюр  прямоугольной с равнодействующей и треугольной с равнодействующей , отстоящей от начала координат на b/6.

Составим уравнения равенства проекций всех сил на вертикальную ось и равновесия моментов относительно начала координат

;

,

где e  эксцентриситет приложения равнодействующей внешней нагрузки P.

Решая систему уравнений, имеем

.

С учетом полученного и (4.89), окончательно запишем

. (4.93)

Нетрудно убедиться, что полученное выражение совпадает с известной из Сопротивления материалов формулой для нормальных напряжений в прямоугольном сечении при внецентренном сжатии:

.

Действительно, P  продольная сила,  площадь сечения,  момент внешних сил в сечении,  момент инерции, x  расстояние от нейтральной оси до рассматриваемой точки.

Решая эту же задачу в пространстве можно вполне аналогично получить

. (4.94)

Заметим, что в приведенном простейшем случае, когда фундамент принимается абсолютно жестким, решение удалось получить, не прибегая к уравнению (4.92), которое используется в общем случае, когда рассматривается фундамент конечной жесткости.

4.8.2. Модель линейно-деформируемого основания

В данной модели при описании работы грунта справедливыми являются все гипотезы ТЛДС (см. п. 4.2.2). Как уже говорилось выше, осадка поверхности будет иметь место не только в точках приложения нагрузки, но и по всей границе основания (рис. 4.34, а).

В случае плоской задачи осадка w(x) поверхности в точке M(x) от силы P  1, приложенной на расстоянии  от начала координат (рис. 4.36, а), будет функцией от аргумента :

.

Пусть на поверхности задана некоторая распределенная нагрузка p() (рис. 4.36, б), тогда осадка от элементарной силы составит

, (4.95)

Проинтегрировав выражение (4.95), получим осадку в рассматриваемой точке от всей нагрузки

Рисунок 4.36.  К определению перемещений точек поверхности от единичной силы (а)

и от распределенной нагрузки (б)

. (4.96)

С учетом полученного выражения уравнение изогнутой оси подошвы фундамента (4.88) примет вид:

. (4.97)

Используя формулу (4.50) для осадки поверхности в задаче Фламана

, (4.98)

перепишем (4.97) в виде

. (4.99)

Напомним, что помимо (4.99) искомая функция p(x) должна также удовлетворять уравнениям равновесия сил и моментов, которые в данном случае имеют вид:

; ,

где P и M  равнодействующая и момент внешних сил.

Коротко рассмотрим результаты некоторых решений в предположении о бесконечно большой жесткости конструкции фундамента (рис. 4.37 а, б, в) [17].

Решение для центрально приложенной нагрузки было получено М. Садовским в 1928 г. (рис. 4.37, а):

, (4.100)

где a  половина ширины фундамента.

В.А. Флориным (1934г.) было дано решение для загружения жесткого фундамента парой сил (рис. 4.37, б):

Рисунок 4.37.  Напряжение по подошве абсолютно жесткого фундамента на линейно-деформируемом основании при различных схемах загружения; 1  эпюра контактных напряжений, рассчитанных по теории линейно-деформируемой среды, 2, 3, 4  трансформация фактической эпюры контактных напряжений при увеличении нагрузки

, (4.101)

где   угол наклона подошвы, E и   модуль деформации и коэффициент Пуассона основания.

Таким образом, при внецентренном загружении суммированием решений (4.100) и (4.101) получим:

. (4.102)

Все три решения обладают следующей особенностью. Как следует из формул (4.100)…(4.102), под краями фундаментов, т.е. при , напряжения равны бесконечности (рис. 4.37, а, б, в). Понятно, что напряжения не могут быть бесконечно большими, поскольку ограничены пределом текучести. Однако качественно полученные эпюры подтверждают тот факт, что разрушение действительно начинается под краями фундаментов.

Реальная эпюра контактного давления по указанной причине отличается от теоретической 1 и показана на рис. 4.37, а, пунктирной линией 2. Отметим, что трансформация реальной эпюры контактных давлений 234 продолжается вплоть до момента разрушения основания, когда она из седлообразной окончательно переходит в выпуклую.

Для фундаментов конечной жесткости выполненные исследования позволили сделать вывод о том, что величина и характер деформаций и напряжений в основании на границе с фундаментом будет определяться, главным образом, соотношением жесткостей грунта и фундамента.

На примере описанной задачи центрально нагруженного абсолютно жесткого фундамента рассмотрим численный метод решения контактной задачи, который в последствие можно обобщить на более сложные случаи.

Согласно (4.50), имеем

, (4.103)

где .

Поставим задачу: по заданной функции w(х) с помощью (4.103) определить функцию р(х). В последнем случае искомая функция входит под знак интеграла и равенство (4.103) превращается в интегральное уравнение. В рассматриваемом случае контактной задачи необходимо определить такой закон контактного давления, при котором в пределах подошвы фундамента осадка w(х)  w₀  const. Для приближенного решения поставленной задачи заменим в (4.103) интегрирование суммированием по способу прямоугольников. С этой целью интервал [a, a] разобьем на n равных частей длиной h  2a/n. Осадку w(х_i) и давление р(х_i) для большей точности будем относить к срединным точкам этих частей, координаты х_i которых определяются равенством

, i  1, 2, … , n.

Ради удобства введем сокращенное обозначение

, , , j  1, 2, … , n.

В результате осадку в точке с координатой х, при известном законе распределения давления р(х_i) приближенно можно определить выражением

.

В контактной задаче, напротив, надо определить контактные давления p₁, p₂, … , p_n. Используя предыдущую формулу, можно для этой цели записать систему n линейных уравнений:

,

(4.104)

где .

К системе (4.104) необходимо добавить уравнение равновесия фундамента :

.

(4.105)

Система уравнений (4.104), (4.105) состоит из n  1 линейных уравнений и содержит столько же неизвестных. К ним кроме известных давлений p_i относится и величина s₀. Решение линейной системы не представляет сложности, в особенности если использовать ЭВМ. Полученная таким путем эпюра контактного давления имеет ступенчатый вид, как показано на рис. 4.38. Очевидно, решение задачи будет тем точнее, чем больше участков взято на контактной поверхности. При n решение будет стремиться к точному решению (4.100), а эпюра контактного давления  к гладкой эпюре.

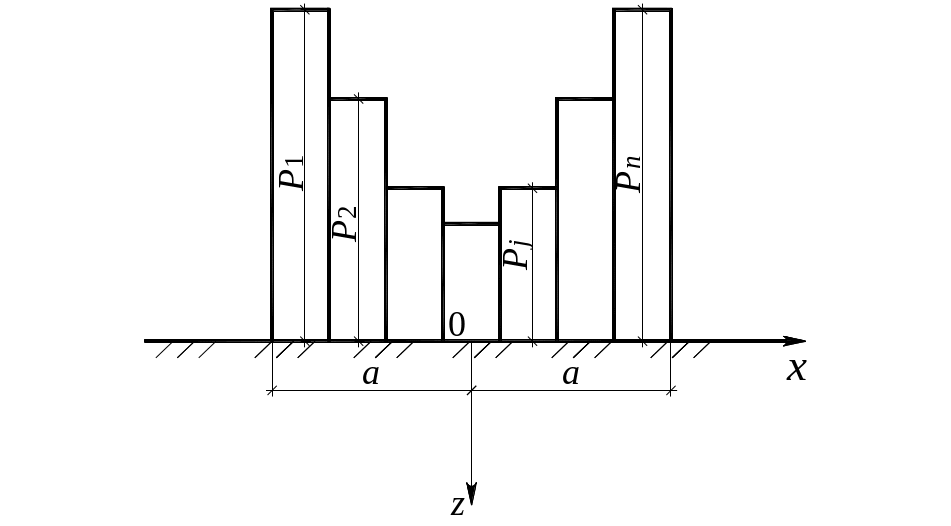
Рисунок 4.38.  К численному методу решения контактной задачи

4.9. Первая критическая нагрузка по проф. Н.П. Пузыревскому, 1923 г.

До сих пор при определении напряженного состояния основания мы не были ограничены величиной задаваемой нагрузки. Формально подставляя в приведенные выше формулы для напряжений сколь угодно большие нагрузки, можно было получать и сколь угодно большие значения напряжений. Ясно, что это не соответствует действительности.

Как следует из фактического характера работы грунта (см. п. 4.1 фазы деформирования по Н.М. Герсеванову), при превышении внешней нагрузкой значения первой критической, в грунтовом основании начинают интенсивно развиваться процессы пластического течения грунта. Поведение грунта уже не подчиняется закону Гука, а основанные на нем решения ТЛДС дают качественно неверные результаты, например, величины осадок основания оказываются сильно заниженными. Кроме того, в самой постановке задач ТЛДС отсутствуют какие-либо критерии, позволяющие оценить степень опасности нагрузки, степень близости напряженного состояния грунта к предельному.

Поставим задачу определить, при каком давлении p в основании начнут возникать области предельного напряженного состояния. Иначе говоря, вопрос заключается в теоретическом расчете величины первой критической нагрузки. Впервые эта задача была рассмотрена проф. Н.П. Пузыревским. Приводимое решение базируется на решении Мичелла и условии КулонаМора, при этом учитывается еще и бытовое напряженное состояние. Сказанное означает, что нагрузка на основание, а следовательно и напряжения, получаемые по ТЛДС, могут возрастать лишь пока не нарушается условие прочности.

Вначале рассмотрим соответствие между реальной и расчетной схемами аналогично тому, как это было сделано в п. 4.7.1. Фундаменты зданий и сооружений практически всегда заглубляются в основание на некоторую глубину d. При определении напряженно-деформированного состояния основания это заглубление может быть учтено приложением равномерного давления q  d к расчетной поверхности основания, проведенной на уровне подошвы фундамента (рис. 4.39).

Рисунок 4.39.  Расчетная схема задачи Пузыревского об областях пластических деформаций в основании от равномерной полосовой нагрузки

Предположим, что фундамент шириной b  2a центрально загружен силой Р и создает равномерное давление на основание интенсивностью р₀ = Р/А (А  площадь подошвы фундамента). Часто фундамент имеет длину, во много раз превышающую его ширину. Теоретически допустимо считать такой фундамент бесконечно длинным и действие его на основание заменить равномерным полосовым давлением, т.е. приходим к условиям плоской деформации.

Заданную систему нагрузок на расчетную поверхность основания можно представить в виде суммы равномерного давления q, действующего на всей поверхности, и равномерного давления р  р₀  q, приложенного в пределах ширины подошвы фундамента. Напряженное состояние в основании от указанной полосовой нагрузки определим с помощью формул Мичелла (4.56):

.

Другая часть напряжения возникает от сплошной равномерной пригрузки q и собственного веса грунта. В произвольной точке основания, расположенной на глубине z от его расчетной поверхности, эта часть напряжений согласно формулам (4.42) и (4.43) составит

, .

Введем гипотезу   1, что отвечает значению коэффициента Пуассона   0,5. В результате получаем гидростатическое бытовое напряженное состояние, в котором все главные напряжения от собственного веса грунта в точке равны между собой

,

и в котором все площадки в точке являются главными. Это следует из того, что при таком напряженном состоянии круг Мора стягивается в точку и на любой площадке . В результате полные главные напряжения можно получить простым суммированием двух указанных частей:

, .

(4.106)

Как было сказано выше, при некотором давлении фундамента в основании возникают области пластических деформаций, в которых напряжения достигают предела текучести грунта. Для того чтобы напряжения в какой-либо точке достигали предела текучести грунта, они должны удовлетворять условию текучести КулонаМора, которое запишем в главных напряжениях

.

Подставим (4.106) в условие КулонаМора. При этом учтем, что

, ,

и тогда получим:

,

или

.

Отсюда выразим координату z:

.

(4.107)

В полученном равенстве z и  определяют точку, в которой имеет место предельное напряженное состояние. Можно определить совокупность таких точек при постоянном значении давления p. Указанная совокупность точек будет представлять собой границу области разрушения основания при данном p, т.е. на этой границе выполнятся условие КулонаМора (круг Мора касается прямой Кулона). В соседних с ней областях грунт либо еще находится в безопасном состоянии (круг Мора «внутри» прямой Кулона), либо будет уже разрушен, поскольку круг Мора здесь пересечет прямую Кулона (рис. 4.39).

Остановимся подробней на геометрии границы зон разрушения. Чтобы получить уравнение, определяющее эти границы, к равенству (4.107) необходимо добавить еще одно выражение, которое связывало бы вторую координату х с углом . Такое выражение можно получить исходя из первого равенства (4.54). Запишем его, используя известное тригонометрическое выражение, в виде

.

Учитывая, что

, ,

получим

.

Отсюда установим искомую зависимость, выразив координату x:

.

(4.108)

Равенства (4.107), (4.108) в совокупности представляют собой параметрическую форму уравнения границ областей пластических деформаций, параметром которого является угол  в интервале 0    .

Исследования уравнений (4.107), (4.108) показывают, что когда фундамент заглублен в основание или расположен на поверхности связного грунта ( ), области пластических деформаций имеют замкнутый вид. Правая область такой формы показана на рис. 4.40 под номером 1. В случае, когда фундамент располагается на поверхности (q = 0) сыпучего (c = 0) основания, области пластических деформаций оказываются разомкнутыми, выходящими на поверхность основания. Правая область такой формы представлена на рис. 4.40 под номером 2.

Рисунок 4.40.  Замкнутая 1 и разомкнутая 2 области пластических деформаций

С практической точки зрения нас, прежде всего, будет интересовать максимальная глубина их развития z_max (см. рис. 4.39). Для определения этой величины поступим согласно общему правилу отыскания экстремума функции. Возьмем производную от (4.107) по  и приравняем ее нулю:

.

Отсюда, поскольку , должно равняться нулю выражение, заключенное в скобки. В результате получаем равенство , из которого следует

.

(4.109)

Подставив это выражение в (4.107), получим формулу для максимальной глубины развития пластических деформаций

.

(4.110)

Полученное уравнение решим относительно внешней нагрузки:

.

(4.111)

Если в (4.111) положить , то получим такое значение нагрузки, при котором впервые начинается разрушение грунта:

.

(4.112)

Выражение определяет (4.112) совершенно безопасное давление на основание, или первую критическую нагрузку по Н.П. Пузыревскому.

Из выражения (4.112) предельным переходом при   0 получим формулу первого критического давления на основание, сложенное идеально связанным грунтом ( ):

.

Последующие исследования показали, что в общем случае первая критическая нагрузка, рассчитанная по формуле (4.112), занижает наблюдаемое в опытах значение. Поэтому в практике проектирования оснований и фундаментов используют не совершенно безопасное давление (4.112), а нагрузку, рассчитываемую по формуле (4.111) при z_max  b / 4, т.е. допускают развитие областей пластических деформаций на глубину в четверть ширины фундамента (рис. 4.39) [25]:

.

(4.113)

В нормах проектирования фундаментов эта величина используется для определения очень важной характеристики  расчетного сопротивления R грунта основания, по которому преимущественно рассчитываются размеры подошвы фундаментов промышленных и гражданских зданий. Обычно для расчетного сопротивления записывают в виде:

.

(4.113)

где M_, M_q, M_c  коэффициенты, зависящие от угла внутреннего трения:

, , .

Отметим две особенности изложенного решения.

Первая особенность заключается в принятии равенства   1 для определения природного напряженного состояния основания, тогда как в действительности коэффициент бокового давления должен быть меньше единицы, а коэффициент Пуассона меньше 0,5. Эта неточность в значительной мере оправдывается тем, что природное напряженное состояние внутри небольших по размерам областей пластических деформаций составляет лишь часть, притом меньшую, общих напряжений. Принятие же в расчет напряжений, определенных как для условий компрессионного сжатия, т.е.  < 0,5, при углах внутреннего трения приводит к нарушению условия прочности даже без внешней нагрузки, а только от действия собственного веса. В этом можно убедиться, подставив выражения (4.42) и (4.43) при q  0 в условие КулонаМора.

Вторая особенность состоит в том, что внутри областей пластических деформаций напряжения превышают предел текучести грунта ( > 0,   функция пластичности), чего, во-первых, не должно быть в действительности (  0  всюду), а во-вторых, если это так, то решения ТЛДС неприменимы. Указанная некорректность, очевидно, тем меньше, чем меньше размеры областей пластических деформаций.

Учитывая рассмотренную нестрогость решения, в практическом его использовании считаются допустимыми области пластических деформаций, удовлетворяющие неравенству .