Самостоятельная работа №1по теме:«Взаимное расположение прямых и плоскостей в пространстве» Вариант I

1 .На рисунке 1 точки М, N, Q и Р — середины отрезков DB, DC, АС и АВ. Найдите периметр четырехугольника MNQP, если AD= 12 см, ВС =14 см.

Рис. 1.

2. Треугольники ABC и ABD не лежат в одной плоскости. Докажите, что любая прямая, параллельная отрезку CD, пересекает плоскости данных треугольников.

3. На сторонах АВ и АС треугольника ABC взяты соответственно точки D и Е так, что DE = 5 см и BD/DA=2/3. Плоскость α проходит через точки B и С и параллельна отрезку DE. Найдите длину отрезка ВС.

4.Через точку М, не лежащую на прямой а, проведены две прямые, не имеющие общих точек с прямой а. Докажите, что по крайней мере одна из этих прямых и прямая а являются скрещивающимися прямыми.

Вариант II

1.Даны параллелограмм ABCD и трапеция ABEK с основанием ЕК, не лежащие в одной плоскости, Найдите периметр трапеции, если известно, что в нее можно вписать окружность и АВ = 22,5 см, EK = 27,5 см.

2. Точка М не лежит в плоскости трапеции ABCD с основанием AD. Докажите, что прямая AD параллельна плоскости ВМС.

3. Точка C лежит на отрезке АВ. Через точку А проведена плоскость, а через точки В и С — параллельные прямые, пересекающие эту плоскость соответственно в точках В1 и С1. Найдите длину отрезка СС1, если: точка С — середина отрезка АВ и ВВ1=7 см.

4. Докажите, что если АВ и CD скрещивающиеся прямые, то AD и ВС также скрещивающиеся прямые.

Критерии оценки: «3» - 2 задачи, «4» - 3 задачи, «5» - 4 задачи

Самостоятельная работа №2по теме:«Параллелипипед и куб» Вариант I

1. Сумма всех ребер параллелепипеда АВСДА₁В₁С₁Д₁ равна 120 см. Найдите каждое ребро параллелепипеда, если , .

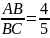2. Изобразите параллелепипед АВСДА₁В₁С₁Д₁ и постройте его сечение плоскостью АВС₁.

3. Докажите, что в параллелепипеде АВСДА₁В₁С₁Д₁плоскость А₁ДВ параллельна плоскости Д₁СВ₁.

4. Через два противолежащих ребра куба проведено сечение, площадь которого равна 64 с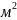 . Найдите ребро куба и егодиагональ.

5. Найдите угол между двумя диагоналями граней куба, имеющими общий конец.

Вариант II

7. Докажите, что диагональ параллелепипеда меньше суммы трех ребер, имеющих общую вершину.

1. Дан параллелепипед АВСДА₁В₁С₁Д₁. Докажите, что АС IIА₁С₁ и ВД II В₁стью АСС₁.

2. По какой прямой пересекаются плоскости сечений А₁ВСД₁ и ВДД₁В₁ параллелепипеда Д₁.

3. АВСДА₁В₁С₁Д₁.Изобразите параллелепипедАВСДА₁В₁С₁Д₁ и постройте его сечение плоско

5. Докажите, что сумма квадратов четырех диагоналей параллелепипеда равна сумме квадратов двадцати его ребер.

6. Ребро куба равно a. Найдите площадь сечения проходящего через диагонали двух его граней.

7. Сколько осей симметрии имеет куб?

Оценка: «3» - 4 задачи, «4» - 5задач, «5» - 6задач

Самостоятельная работа №3по теме:«Призма» Вариант I

1. Докажите, что у прямой призмы все боковые грани – прямоугольники.

2. Сторона основания правильной треугольной призмы равна 8 см, боковое ребро равно 6 см. Найдите площадь сечения, проходящего через сторону верхнего основания и противолежащую вершину.

3. Основанием прямой призмы является равнобедренная трапеция с основаниями 25 см и 9 см и высотой 8 см. Найдите двугранные углы при боковых ребрах призмы.

4. Диагональ правильной четырехугольной призмы образует с плоскостью боковой грани угол в 30 . Найдите угол между диагональю и плоскостью основания.

5. Докажите, что площадь боковой поверхности наклонной призмы равна произведению периметра перпендикулярного сечения на боковое ребро.