
- •Глава1 кратные интегралы
- •1.1. Двойные интегралы
- •1.1.1. Лабораторная работа 1 непосредственное вычисление двойных интегралов
- •1.1.2 Лабораторная работа 2
- •1.1.4. Лабораторная работа 4
- •1.2. Тройные интегралы.
- •1.2.1. Лабораторная работа 1
- •1.2.2. Лабораторная работа 2
- •2.1.1. Лабораторная работа
- •2.1.2. Лабораторная работа 2
- •2.2. Поверхностные интегралы
- •2.2.1. Лабораторная работа №1 Поверхностные интегралы
- •Задания:
- •Ответы:
- •Литература
Государственный комитет Российской Федерации
По высшему образованию
Калмыцкий государственный университет
КРАТНЫЕ, ПОВЕРХНОСТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
Лабораторные работы по математическому анализу
Элиста 2011
Глава1 кратные интегралы
1.1. Двойные интегралы
1.1.1. Лабораторная работа 1 непосредственное вычисление двойных интегралов
ri+1



 Пусть
D
замкнутая ограниченная область с
границей r:
Sr=0,
функция f(x,y)
ограниченна в области D.
Разобьём область D
конечным числом кривых ri:Sri=0
на частичные области Di
, i=1,2..r.
Эти области Di
квадрируемые, т.е. имеют площадь.
Пусть
D
замкнутая ограниченная область с
границей r:
Sr=0,
функция f(x,y)
ограниченна в области D.
Разобьём область D
конечным числом кривых ri:Sri=0
на частичные области Di
, i=1,2..r.
Эти области Di
квадрируемые, т.е. имеют площадь.
О
Di
r бозначим
через ΔDi
ПЛОЩАДЬ ЧАСТИЧНОЙ
бозначим
через ΔDi
ПЛОЩАДЬ ЧАСТИЧНОЙ
О
ri

 БЛАСТИ
Di
через di=
БЛАСТИ
Di
через di=
![]() и назовём
и назовём
Д ИАМЕТРОМ
РАЗБИЕНИЯ области D
на
ИАМЕТРОМ
РАЗБИЕНИЯ области D
на
ч астичные
области Di.
В каждой частичной области
астичные
области Di.
В каждой частичной области
D i
возьмём точку Mi
и составим сумму :
i
возьмём точку Mi
и составим сумму :

![]()
Эта
сумма называется ИНТЕГРАЛЬНОЙ СУММОЙ
функции f(x,y)
при разбиении области D
на частичные области Di
и выборе точек Mi
из частичных областей Di
![]() зависит от разбиения и выбора точки
MiÎDi
зависит от разбиения и выбора точки
MiÎDi
def1:
Число I
называется ПРЕДЕЛОМ ИНТЕГРАЛЬНОЙ СУММЫ
при d®0
области D
на частичные области Di
на частичные области Di
![]() если для "e>0,
$
d>0,
что для "
разбиения области D
на частичные области Di
с диаметром d<d
и для "
набора точек MiÎDi
выполняется
условие:
если для "e>0,
$
d>0,
что для "
разбиения области D
на частичные области Di
с диаметром d<d
и для "
набора точек MiÎDi
выполняется
условие:
![]()
def2: Если существует конечный предел при d®0, то говорят, что функция f(x,y) ИНТЕГРИРУЕМА по области D т.е. fÎR(D), а этот предел называется ДВОЙНЫМ ИНТЕГРАЛОМ от функции f(x,y) по области D
![]()
Если область D задана неравенствами a£x£b y1(x)£y£y2(x), где y1(x), y2(x) интегрируемые функции на [a,b], то соответствующий двойной интеграл может быть вычислен по формуле:

следующие свойства двойных интегралов
1)
![]()
2)
![]() ,
где С=const.
,
где С=const.
3) Если область интегрирования D разбита на две области D1 и D2, то
![]()
Пример1
Вычислить

Решение:
![]()
Пример2:
Вычислить![]() ,
если область D
ограниченна линиями:
,
если область D
ограниченна линиями:
y= 2-x2 , y= 2x-1
Решение: построим область D. Первая линия- парабола, симметричная относительно оси Oy с вершиной в точке (0,2) Вторая линия- прямая.
Р
у=2х-1
2![]()
н айдём
координаты точек
айдём
координаты точек
пересечения A и B: A(-3;-7), B(1,1)

у=2-х2

![]()
Пример3: Поменять порядок интегрирования

Решение:
область интегрирования ограничена
линиями: x=-1,
x=1,
y=
1-x2,
![]() .
Изменим порядок интегрирования, для
чего заданную область представим в виде
двух областей D1
огран. слева и справа ветвями параболы
.
Изменим порядок интегрирования, для
чего заданную область представим в виде
двух областей D1
огран. слева и справа ветвями параболы
![]() ,
ограниченную дугами окружности
,
ограниченную дугами окружности
![]() .
Тогда
.
Тогда

Задания
1) Вычислить
1.
![]()
2.
![]()
3.

4.
![]()
5.

6.

7.
![]()
8.
![]()
9.
![]()
10.

2) Вычислить
 ,
где
,
где

 ,
где P ограниченна
линиями
,
где P ограниченна
линиями

 ,
где P ограниченна
линиями
,
где P ограниченна
линиями
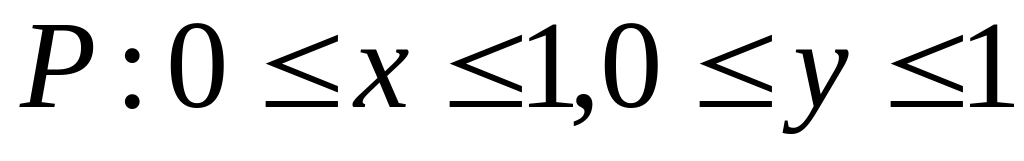
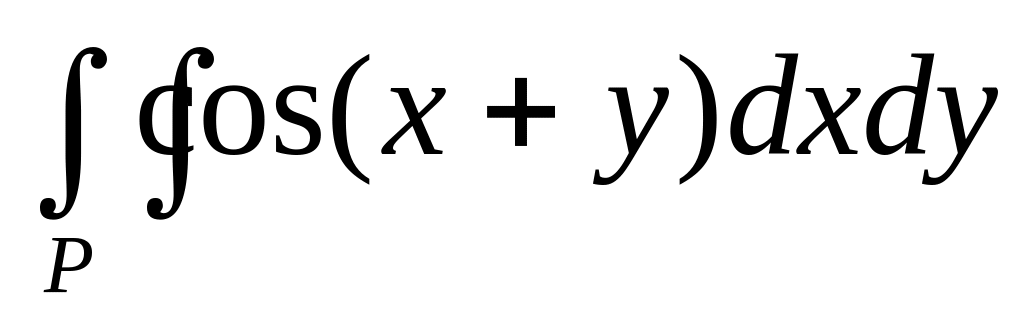 ,
обл Р
ограниченна
прямыми х=0,
у=х,
,
обл Р
ограниченна
прямыми х=0,
у=х,
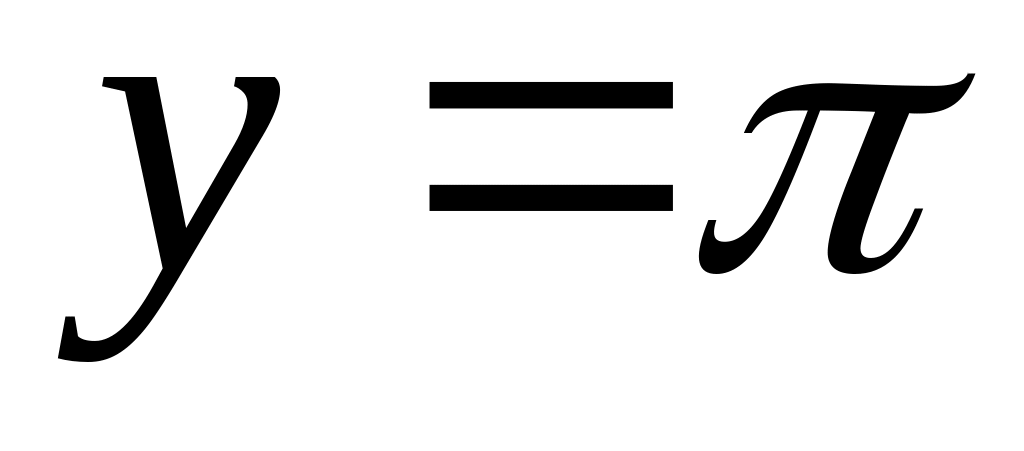

 ,
где P ограниченна
линиями
,
где P ограниченна
линиями

 ,
где D
ограниченна линиями х=2,
у=х, ху=1
,
где D
ограниченна линиями х=2,
у=х, ху=1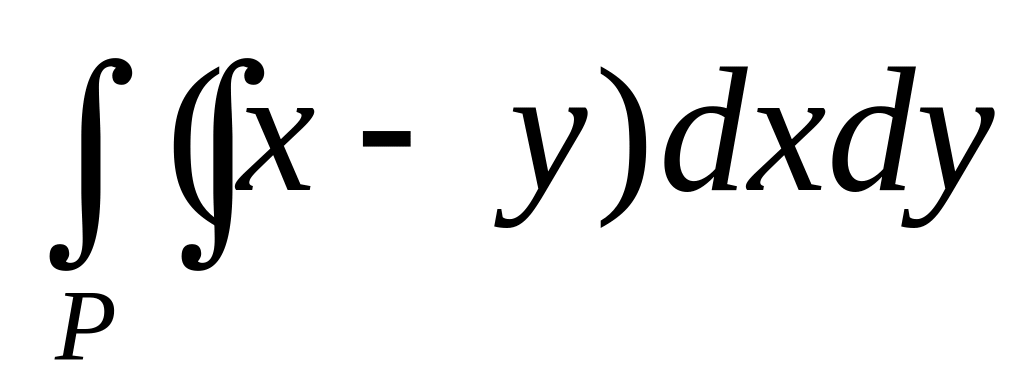 ,
где Р
ограниченна линиями у=0,
у=х, х+у=2
,
где Р
ограниченна линиями у=0,
у=х, х+у=2

3) Поменять порядок интегрирования
4)
Расставить пределы интегрирования в
том и в другом порядке в двойном интеграле
![]() для указанных областей S:
для указанных областей S:
S трапеция с вершинами О(0;0),А(2;0), В(1;1), С(0;1).
S прямоугольник с вершинами О(0;0),А(2;0), В(2;1), С(0;1).
S треугольник с вершинами О(0;0),А(1;0), В(1;1)..
S параллелограмм с вершинами А(1;2), В(2;4), С(2;7),D(1;5).
S круговой сектор ОАВ с центром в точке О(0;0), у которого концы дуги А(1;1), В(-1;1).
S круговое кольцо, ограниченное окружностями радиусов r=1 и R=2 c общим центром (0;0).
Область S заданна неравенством
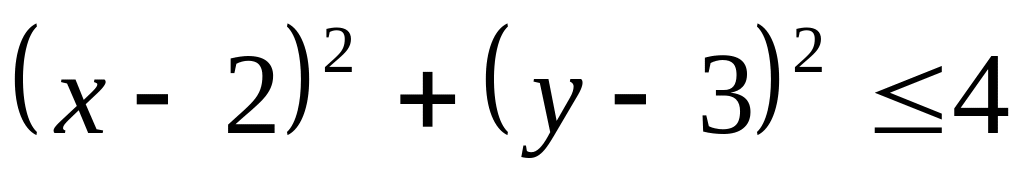
Область S ограниченна линиями

S ограниченна гиперболой
 (имеется ввиду область, содержащая
начало координат).
(имеется ввиду область, содержащая
начало координат).область S ограниченна линиями х=0, у=0,


Ответы
1)
1.
![]() 2) 1. 1
2) 1. 1
2.
![]() 2. 4а
2. 4а
3. 50,4 3. (е-1)2
4.
![]() 4. -2
4. -2
5.
![]() 5.
5.
6.
![]() 6.
6.
![]()
7.
![]() 7.
7.
8.
![]() 8.
8.
![]()
9.
![]() 9.
9.
![]()
10.
![]() 10. 1
10. 1




