2 Определение динамических свойств звеньев по частотным характеристикам

Рассмотрим частотные характеристики системы первого порядка, передаточная функция которой имеет вид:

(передаточная функция для апериодического звена из табл. 1),

s = iω,

где i – мнимое комплексное число.

Заменим оператор s:

.

Разложим на вещественную и мнимую часть (умножим числитель и знаменатель на сопряженное число):

;

i² = – 1;

.

Чтобы разделить комплексное число на действительное необходимо вещественную часть и комплексную часть поделить на эти числа:

Частотная функция этой системы:

,

Построим график функции |W(iω)| и |W(iω/Т)|:

ω
|W(iω)|
|W(iω/Т)|

Иллюстрация полосы пропускания

Построим график амплитудно-фазовой характеристики (АФЧХ) зависящей от частоты колебаний (ω):

ω
W(iω)

Амплитудная и фазовая характеристики определяются выражениями.

Амплитудная характеристика:

ω
А(ω)

Фазовая характеристика:

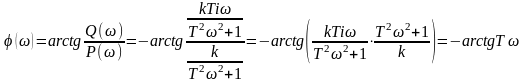
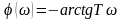
ω
φ(ω)

Рассчитаем логарифмическую амплитудную характеристику (ЛАХ):

ω	-2	-1	0	1	2
L(ω)

3 Определение показателей качества переходного процесса по логарифмическим частотным характеристикам

По полученным графикам ЛАХ и ЛФХ определяем основные динамические характеристики элементарных звеньев: t_П – время переходного процесса, σ% – перерегулирование, T_k – период колебаний при переходном процессе, δ – статическая ошибка регулирования.

Время переходного процесса при δ = 0,05x_ss определяется по формуле

где ω_s – частота сопряжения.

Период колебаний (для колебательного звена)

Существует аналитическая связь между величиной перерегулирования и величиной ∆L(ω_s) = L(ω_s)−L(0). Соотношения между ∆L(ω_s) и величиной перерегулирования в табл. 5, эти данные используем для определения σ.

Время переходного процесса определяется для всех звеньев по ω_s, кроме неустойчивых звеньев, где условно принимается t_П → ∞, и идеальных интегрирующих и дифференцирующих, где условно принимается t_П → 0.

Вывод:

Практическая работа № 3

Исследование устойчивости систем автоматического регулирования.

Оценка качества регулирования

Цель работы: применение критериев устойчивости для исследования систем автоматического регулирования, определение показателей качества регулирования систем.

Понятие устойчивости системы регулирования связано с ее способностью возвращаться в состояние равновесия после исчезновения внешних сил, которые вывели ее из этого состояния.

1 Критерий устойчивости Рауса-Гурвица

Критерий Рауса-Гурвица используется при анализе устойчивости линейных стационарных систем. Он позволяет аналитически определить, все ли корни полинома имеют отрицательные действительные части.

Вещественные части корней будут отрицательными в том случае, если все коэффициенты уравнения и диагональные миноры главного определителя будут положительными. Главный определитель составляется так, что по главной диагонали выписываются коэффициенты уравнения начиная с a₁ в возрастающем порядке до a_n. От каждого коэффициента главной диагонали по вертикали вверх выписываются коэффициенты с возрастающими и вниз - с убывающими индексами. Места в матрице коэффициентов с индексами больше n и меньше 0 заполняются нулями.

Критерий Гурвица формируется следующим образом:

для того, что бы АСУ была устойчива, необходимо и достаточно, что бы все определители Гурвица (∆₁, ∆₂, …, ∆_n) были положительными, и при этом выполнялось условие а₀>0.

Рассмотрим выражение критерия Гурвица для характеристического уравнения третьего порядка

a₀s³+ a₁s²+a₂s+a₃ = 0

Главный определитель

Условие Гурвица

> 0

Следовательно, система будет устойчивой, если все коэффициенты a₀,a₁,a₂,a₃ положительны и a₁a₂ −a₀a₃ > 0, и a₀ > 0.