
- •Лекція 1 (2 год.) Основні символьні позначення, домовленості, означення і приклади об’єктів дослідження математичної статистики Питання, які розглядаються в лекції:
- •1.1. Сукупності
- •1.2. Ознаки
- •1.3. Шкали
- •1.3.1. Номінальні шкали
- •1.3.2. Порядкові шкали
- •1.3.3. Числові шкали
- •1.3.4. Дискретні та неперервні шкали
- •1.3.5. Інтервальні та пропорційні шкали
- •1.3.6. Рівномірні шкали
- •1.4. Якісні та кількісні ознаки
- •1.5. Ранжування
Лекція 1 (2 год.) Основні символьні позначення, домовленості, означення і приклади об’єктів дослідження математичної статистики Питання, які розглядаються в лекції:
Вступ
1.1. Сукупності
1.2. Ознаки
1.3. Шкали
1.3.1. Номінальні шкали
1.3.2. Порядкові шкали
1.3.3. Числові шкали
1.3.4. Дискретні та неперервні шкали
1.3.5. Інтервальні та пропорційні шкали
1.3.6. Рівномірні шкали
1.4. Якісні та кількісні ознаки
1.5. Ранжування
Висновки
Література
Бешелев С. Д. Математико-статистические методы экспертных оценок / С. Д. Бешелев, Ф. Г. Гурвич. – М. : Статистика, 1980.
Вайнберг Док., Статистика / Док. Вайнберг, Дж. Шуменер: Пер. с англ. – М. : Статистика, 1979.
Гласс Дж., Статистические методы в педагогике и психологии / Дж. Гласс, Дж. Стенли: Пер. с англ. – М. : Прогресс, 1976.
Громыко Г. Л. Статистика / Г. Л. Громыко. – М. : Изд-во МГУ, 1981.
Захаров В. П. Применение математических методов в социально-психологических исследованиях / В. П. Захаров. – Л. : Изд-во ЛГУ, 1985.
Кендалл М. Дж. Статистические алгоритмы в социологических исследованиях / М. Дж. Кендалл, А. Стюарт. – Новосибирск: Наука, 1985.
Кимбл Г. Как правильно пользоваться статистикой / Г. Кимбл: Пер. с англ. – М. : Финансы и статистика, 1982.
Лбов Г. С. Методы обработки разнотипных экспериментальных данных / Г. С. Лбов. – Новосибирск : Наука, 1981.
Максименко В. С. Статистичний аналіз соціологічних даних / В. С. Максименко, В. I. Паніотто, Н. М. Харченко. – К. : Видав. дім «КМ Академія», 2004.
Математическая статистика: Учебник. – М. : Высш. шк., 1981.
Мюллер П. Таблицы по математической статистике / Мюллер П., Нойман, Шторм Р.: Пер. с нем. – М. : Финансы и статистика, 1982.
Окунь Я. Факторный анализ / Я. Окунь: Пер. с польск. – М. : Статистика, 1974.
Паниотто В. И. Количественные методы в социологии / В. И. Паниотто, В. С. Максименко. – К. : Наук. думка, 1982.
Паповян С. С. Математические методы в социальной психологии / С. С. Паповян. – М. : Наука, 1983.
Практикум з теорії ймовірності та математичної статистики: Навч. посіб. / Р. К. Чорней, О. Ю. Дюженкова, О. Б. Жильцов та ін.; За ред. Р. К. Чорнея. – К. : МАУП, 2003.
Рунион Р. Справочник по непараметрической статистике / Р. Рунион. – М.: Финансы и статистика, 1982.
Сидоренко Е. В. Методы математической обработки в психологии / Е. В. Сидоренко. – СПб. : Речь, 2001.
Суходольский Г. В. Основы математической статистики для психологов / Г. В. Суходольский. – Л. : Изд-во ЛГУ, 1972.
Толстова Ю. Н. Анализ социологических данных / Ю. Н. Толстова. – М. : Науч. мир, 2000.
Турчин В. М. Математична статистика: навч. посіб. / В. М. Турчин. – К. : Видав. центр «Академія», 1999.
Фелингер А. Ф. Статистические алгоритмы в социологических исследованиях / А. Ф. Фелингер. – Новосибирск : Наука, 1985.
Феллер В. Введение в теорию вероятностей и ее приложения: В 2 т. – М. : Мир, 1964, 1967.
Хастинг Н. Справочник по статистическим распределениям / Н. Хастинг, Дж. Пикон: Пер. с англ. – М. : Статистика, 1980.
Холлендер М. Непараметрические методы статистики / М. Холлендер, Д. А. Вулф : Пер. с англ. – М. : Финансы и статистика, 1983.
Эренберг А. Анализ и интерпретация статистических данных / А. Эренберг. – М. : Финансы и статистика, 1981.
D. Essentials of econometrics / D. Gujarati. – N.Y. : McGraw-НіІІ, 1992.
Вступ
Є усталені твердження про поділ усіх наук на дві великі групи – природничі та гуманітарні. Узвичаїлась також думка про те, що одні люди легко сприймають природничі науки, а інші схильні до гуманітарних наук. Хоча відомо багато прикладів щодо історичних постатей, які спростовують ці твердження й думки.
На думку авторів, з природничих наук «найприродничішою» є математика, а з гуманітарних «найгуманітарнішою» – філософія. Видається, ніби філософ не може цікавитись математикою, а математик – філософією. Проте й математик, і філософ помітять з-поміж попередників одні й ті самі прізвища: Рене Декарт, Готфрід Лейбніц, Ісаак Ньютон, Блез Паскаль та ін. Відомо й багато інших науковців, чиї «природничі» та «гуманітарні» здібності гармонійно поєднувалися. Поетами були математик П’єр Ферма і хімік Михайло Ломоносов, художником – математик та інженер Леонардо да Вінчі, письменником – математик Льюїс Керролл. Визнаний «король» математики Карл Гаус знав усі класичні європейські мови. До 19 років він вагався, чому присвятити життя – філології чи математиці.
Чому ж все таки загальноприйнято протиставляти природничі й гуманітарні науки? Доводиться визнати, що є кілька причин. Переважна їх більшість криється в минулому. Річ у тому, що до XIX ст. включно математика, фізика, хімія й інші природничі науки, з одного боку, і філософія, соціально-політичні, соціально-економічні та інші гуманітарні науки – з іншого розвивалися здебільшого окремо.
Лише іноді гуманітарні науки брали «на озброєння» окремі популярні «природничі» відкриття.
Проте у XX ст. ситуація змінилася. Природничі науки, а насамперед математика, почали масований наступ на гуманітарні. Першою «постраждала» економіка. До середини минулого століття в економіці виокремилося кілька дисциплін, які інтенсивно й ефективно почали застосовувати математичні методи. Наступною «жертвою» стала соціологія. У повоєнні роки в соціологію було привнесено низку математичних методів, які вже застосовувалися в економічних науках.
Відомо багато науковців, які привнесли математичні методи в соціально-економічні науки. Серед них є й лауреати Нобелівської премії, зокрема Рагнар Фріш, Пол Самюельсон, Джон Хікс, Кеннет Ерроу, Леонід Канторович, Бертін Фрідмен, Тьяллінг Купманс, Бертін Олін, Герберт Саймон, Джерард Дебре, Амартія Сен.
У сучасних «гуманітарних» науках математика використовується доволі ефективно. Є навіть «математико-гуманітарні» дисципліни. Зокрема, в економіці – економетрія, дослідження операцій, мікроекономіка, фінансовий аналіз, актуарна математика, теорія прийняття рішень, теорія ігор, у соціології – кількісні методи соціологічних досліджень, математичні моделі соціальних процесів, теорія соціального вибору, у мовних науках – математична лінгвістика, у психології – статистичні дослідження та ін.
Сучасна наука вже вийшла за межі, коли для повноцінної дослідницької діяльності науковцю-гуманітарію достатньо було глибоко знати «власну» галузь. Нині він має знати комплекс методів з багатьох інших галузей, у тому числі й природничих. Зокрема, він має бути до певної міри математиком. А для цього необхідно ознайомитись з основними математичними методами, що використовуються в «його» науці. Допомогти цьому й покликана навчальна дисципліна «Математичні методи в психології.
У цій навчальній дисципліні не наводитиметься весь спектр математичних методів, які використовують науковці-гуманітарії. Розглянемо лише невеликий підрозділ математики – математичну статистику – і спробуємо описати її можливі застосування в нематематичній сфері.
Єдине узагальнення, якого зроблено спробу досягти в навчальній дисципліні, полягає в такому. Є дві важливі науки, які вивчають поведінку людини. На рівні суспільства – це соціологія, на індивідуальному рівні – психологія. Отже, спробуємо поєднати ці два напрями дослідження людини в контексті застосування одних і тих самих математико-статистичних методів. Одразу зауважимо, що це поєднання доволі умовне.
З одного боку, у соціологічному дослідженні на відміну від психологічного частіше вдається одержати репрезентативну вибірку. З іншого боку, типові задачі, які доводиться розв’язувати психологам та соціологам, дещо різняться. Крім того, психологи, застосовуючи статистичні методи, часто змушені нехтувати деякими умовами, які формально мають виконуватись. Усе це вносить деяку специфіку у використання математико-статистичних методів у цих галузях.
Для дослідження поведінки людини використовують багато різних математичних методів. У переважній більшості сучасних практичних і наукових літературних джерел соціально-психологічного напряму для аналізу досліджуваних проблем застосовують різні розділи математики, часом надто абстрактні. А один розділ – математичну статистику – використовують найчастіше.
Інтенсивне застосування в соціально-психологічних науках методів математичної статистики пов’язано насамперед з природою поведінки людини. Поведінку людини неможливо описати достеменно точно, вона не детермінована. Людина не повною мірою передбачувана у вчинках як на індивідуальному, так і на глобальному суспільному рівні.
Отже, кожна особа унікально індивідуальна. Немає двох ідентичних людей. Тому, намагаючись описати найважливіші властивості, притаманні певній групі людей, необхідно знайти й виокремити такі їхні характеристики, які найчастіше виявляються у групі.
З огляду на це поведінку людини і суспільства зазвичай описують за допомогою ймовірнісних підходів. Закономірності стохастичної природи виявляються в багатьох аспектах індивідуального та суспільного життя. А математична статистика забезпечує методи аналізу сукупностей даних ймовірнісної природи.
Розглянемо основні методи математичної статистики, які застосовуються в соціології та психології. При цьому акцентуватимемо увагу на практичних аспектах застосування цих методів, нехтуючи часом теоретичним обґрунтуванням.
Основні символьні позначення
Насамперед наведемо основні символьні позначення, які використовуватимемо далі:
+, – – операції додавання та віднімання;
 –
операція
множення;
–
операція
множення;
/ – операція ділення;
= – дорівнює;
 –
приблизно
дорівнює;
–
приблизно
дорівнює;
~ – поводиться подібно чомусь;
X2 – верхній індекс означає піднесення до степеня;
(а; b) – інтервал значень, які лежать між числами а та b;
[а; b] – інтервал значень, більших від числа а і не менших від числа b;
–
символ
належності (наприклад,
 означає,
що х
>
1
і
х
<
8);
означає,
що х
>
1
і
х
<
8);
 –
великими
латинськими літерами позначаються
ознаки;
–
великими
латинськими літерами позначаються
ознаки;
 –
великими
латинськими літерами з нижнім індексом
позначаються елементи сукупності;
–
великими
латинськими літерами з нижнім індексом
позначаються елементи сукупності;
 –
абсолютне
значення числа х;
–
абсолютне
значення числа х;
 –
операція
округлення числа х
до
найближчого меншого цілого;
–
операція
округлення числа х
до
найближчого меншого цілого;
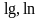 –
логарифми
десятковий та натуральний;
–
логарифми
десятковий та натуральний;
 – символ
нескінченності.
– символ
нескінченності.
