
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
ЛИПЕЦКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
КАФЕДРА АВТОМАТИЗИРОВАННЫХ СИСТЕМ УПРАВЛЕНИЯ
Лабораторная работа №4
«Определение стационарного режима при моделировании на GPSS»
по дисциплине
«Моделирование систем»
Вариант 9, 4
|
|
Студент |
|
|
|
Дырдин Н.В. |
| ||||||||||
|
|
|
|
подпись, дата |
|
фамилия, инициалы |
| ||||||||||
|
|
Группа |
|
АС-09 |
|
|
| ||||||||||
|
|
|
|
|
|
|
| ||||||||||
|
|
Принял |
|
|
|
|
| ||||||||||
|
|
|
|
|
|
Гаев Л.В. |
| ||||||||||
|
|
ученая степень, звание |
|
подпись, дата |
|
фамилия, инициалы |
| ||||||||||
Липецк 2012
Задание кафедры
Определить интервалы времени моделирования, после завершения которых можно говорить о установившемся стационарном режиме. Исследования проводить при различных загруженностях прибора.
Закон распределения дискретной случайной величины (4):
|
Возможные значения |
a |
2a |
3a |
4a |
|
Вероятности |
0.4 |
0.45 |
0.08 |
0.07 |
Закон распределения непрерывной случайной величины (9):
|
xi |
d |
(4d+e)/5 |
(3d+2e)/5 |
(2d+3e)/4 |
(d+4e)/5 |
e |
|
yi |
0 |
Y |
0 |
0 |
Y |
0 |
2. Подбор параметров
Рассмотрим непрерывный закон распределения.
Мат. ожидание:
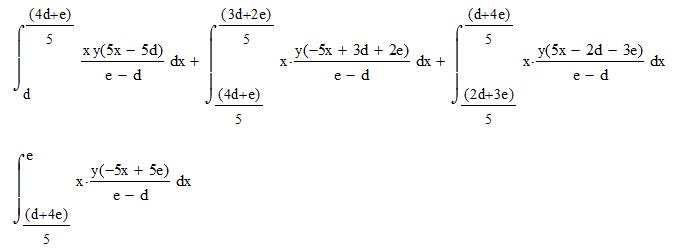
M(P) = y(e^2 – d^2)/5
Площадь должна быть равна 1:
2y*(e-d)/5=1, y=5/(2e-2d).
Примем e=300, d=50. Тогда y=0,01. M(x)=175.
Функция плотности распределения:


Функция распределения случайной величины:


Рассмотрим дискретный закон. Его мат. ожидание:
M(X)=0,4a+0,9a+0,24a+0,28a=1,82a
Теперь подберем параметры непрерывного распределения таким образом, чтобы

|
a |
M(X)н |
M(X)д |
Загр. Прибора |
|
137 |
175 |
249,34 |
0,7 |
|
120 |
175 |
218,4 |
0,8 |
|
107 |
175 |
194,74 |
0,9 |
|
101 |
175 |
183,82 |
0,95 |
|
97 |
175 |
176,54 |
0,99 |
Код программы на языке gpss/pc Система с загруженностью 0,7
GEN1 FUNCTION RN1,D4
.4,137/.85,274/.93,411/1,548
ADV1 FUNCTION RN2,C26
0,50/.01,60/.04,70/.09,80/.16,90/.25,100/.34,110/.41,120/.46,130/
.49,140/.5,150/.5,160/.5,170/.5,180/.5,190/.5,200/.51,210/.54,220/
.59,230/.66,240/.75,250/.84,260/.91,270/.96,280/.99,290/1,300
1 GENERATE FN$GEN1
2 QUEUE OCH
3 SEIZE PRB
4 DEPART OCH
5 ADVANCE FN$ADV1
6 RELEASE PRB
7 TERMINATE
8 PLOT QT$OCH,400,0,80000
9 GENERATE 100000,0
10 TERMINATE 1
START 1
При моделировании появится окно, в котором будет графически отображаться значение среднего времени пребывания в очереди.

Из графика видно, что стационарный режим наступает в момент времени после 60 000. Запустим программу еще раз, и в окрестности этого времени прогоним пошагово. Последний раз среднее время пребывания в очереди случается в момент времени 80000, далее система работает в стационарном режиме.
GPSS/PC Report file REPORT.GPS. (V 2, # 37471) 04-19-2012 09:38:29 page 1
START_TIME END_TIME BLOCKS FACILITIES STORAGES FREE_MEMORY
0 80000 9 1 0 17328
LINE LOC BLOCK_TYPE ENTRY_COUNT CURRENT_COUNT RETRY
1 1 GENERATE 324 0 0
2 2 QUEUE 324 1 0
3 3 SEIZE 323 1 0
4 4 DEPART 322 0 0
5 5 ADVANCE 322 0 0
6 6 RELEASE 322 0 0
7 7 TERMINATE 322 0 0
9 8 GENERATE 1 0 0
10 9 TERMINATE 1 0 0
FACILITY ENTRIES UTIL. AVE._TIME AVAILABLE OWNER PEND INTER RETRY DELAY
PRB 323 0.697 172.81 1 324 0 0 0 1
QUEUE MAX CONT. ENTRIES ENTRIES(0) AVE.CONT. AVE.TIME AVE.(-0) RETRY
OCH 3 2 324 180 0.27 67.33 151.49 0
