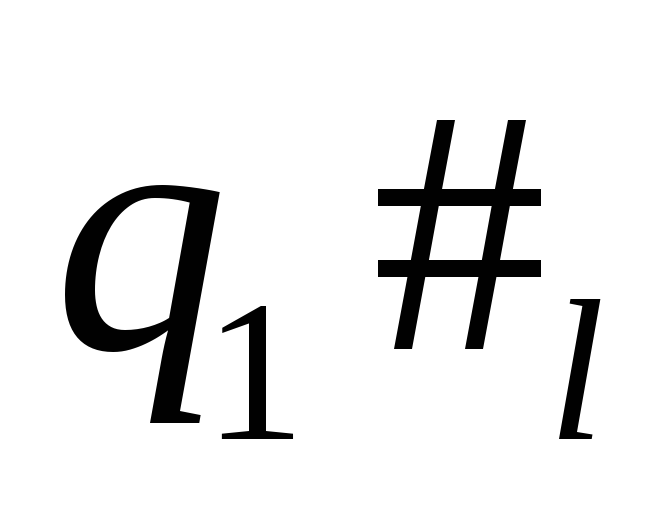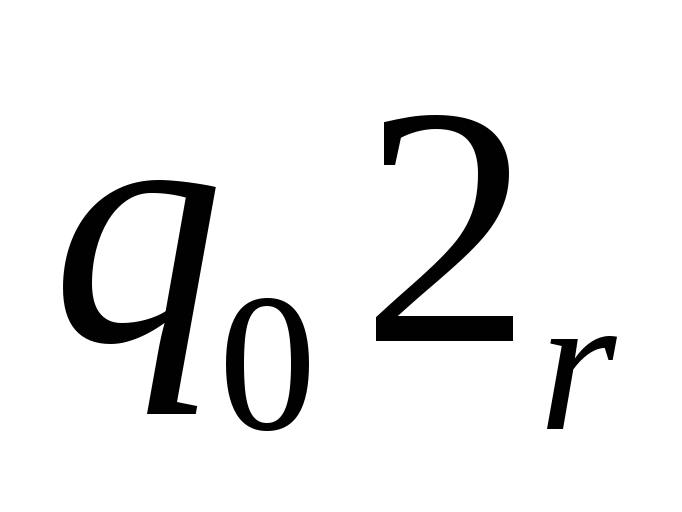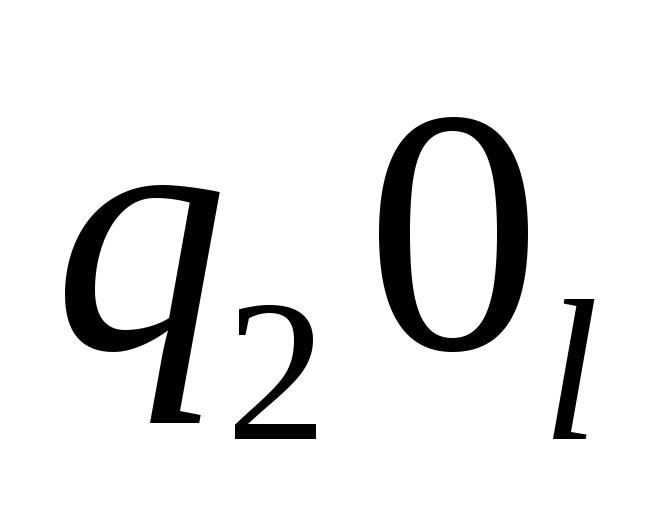16

Практическое занятие №1

1. Найти язык, порождаемый грамматикой:

1. S→aA

2. A→a

3. A→B

4. B→bB

5. B→b

В виде дерева:

S

aA

aaaB

ababB…

L={aa}{ n=1,2,3,…}

2. Найти язык, порождаемый грамматикой:

1. S→aBa

2. A→aBa

3. A→a

4. B→bAB

5. B→b.

В виде дерева:

S

aBa

abaabABa

ababaababaBa

abababa

L={n=1,2,…}

L={n=1,2,…}

3. а) Построить грамматику, порождающую язык L={ n=1,2,…}

S→A,A→aA,A→a

б) Построить грамматику, порождающую язык L={ n=1,2,…}

S→aBa,B→aBa,B→b

в) Построить грамматику, порождающую язык L={ n, m=1,2,…}

S→aAa,A→aAa,A→B,B→bB,b→B

г) Построить грамматику, порождающую язык L={ n=1,2,…}

S→A,A→ab,A→aAb

д) Построить грамматику, порождающую язык L – все натуральные числа в двоичной системе счисления, без незначащих нулей.

S→aA,A→A0,A→A1,A→1

Другой способ:

S→1,S→1A,A→1A,A→0A,A→1,A→0

Домашнее задание.

1. Найти грамматику, порождающую язык L – все вещественные двоичные числа без незначащих нулей.

2. Найти грамматику, порождающую язык L – все цепочки, состоящие из символов a и b, нечетной длины ≥3, причем первый и последний символ совпадают.

3. Найти грамматику, порождающую язык L ={n=1,2,…}.

Практическое занятие №2

1. Используя Б.Н.Ф. – нотацию, описать язык L ={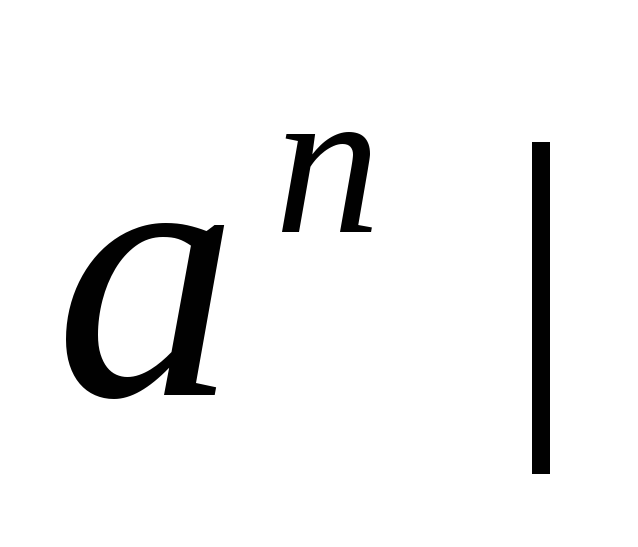n=1,2…}.

L::=a[a{a}*]

L::=a{a}*

L::={a}⁺

2. L={a,b}*\{ε}

L::={a|b}⁺

3. L={α{a,b}*| | α |=2n, n=1,2…}

L::={[a|b] [a|b]}⁺

4. Используя Б.Н.Ф. – нотацию, задать все вещественные положительные десятичные числа без незначащих нулей.

L::=[[1|2|3|4|5|6|7|8|9|.{0|1|2|3|4|5|6|7|8|9}*].{0|1|2|3|4|5|6|7|8|9}⁺]

Другой способ записи:

<з_цифра>::= 1|2|3|4|5|6|7|8|9|

<цифра>::= 0|<з_цифра>

L::= [<з_цифра>.{<цифра>}*].[[<з_цифра>]{<цифра>}*] | [0].{<цифра>}*<з_цифра>}]

5. Используя Б.Н.Ф. – нотацию, задать все цепочки символов a и b, содержащие хотя бы одну цепочку aa.

L::={a|b}*[a][a] {a|b}*

Практическое занятие №3

1. Дан конечный автомат

Определить конечные состояния, если подается:

1) 2)3)4)5)

1. если n– четное, то , еслиn– нечетное, то

2. 

3. 

4. 

5. 

2. Построить конечный автомат, распознающий язык , n>0.

3. Построить конечный автомат, распознающий все двоичные натуральные числа кратные двум.

Принимающее состояние .

4. Построить конечный автомат, распознающий все двоичные натуральные числа кратные четырем.

Принимающее состояние .

5. Построить конечный автомат, , распознающий язык L, состоящий из цепочек с символами a и b, в которых количество символов b кратно 3.

Принимающее состояние .

6. Построить конечный автомат, , распознающий язык L, состоящий из цепочек с символами a и b, содержащих подцепочки aba.

Принимающее состояние .

Домашнее задание:

1. Построить конечный автомат, , распознающий язык L, состоящий из цепочек с символами a и b, в которых количество a четно, b кратно 3.

2. Построить конечный автомат, , распознающий язык L, состоящий из цепочек с символами 0,1,2.Натуральное число в троичной системе счисления, кратное 2.

3. Построить конечный автомат, , распознающий язык L, состоящий из цепочек с символами 0,1,2.Натуральное число в троичной системе счисления, кратное 3.

Практическое занятие №4.

1. На ленте записана цепочка символов a и b. Необходимо всю цепочку заменить на , если количество символов четно, и на, если нечетно.

	a	b	#

2. На ленте записана цепочка символов a и b. Необходимо всю цепочку заменить на , если количество символов четно, и на, если нечетно.

	a	b	#

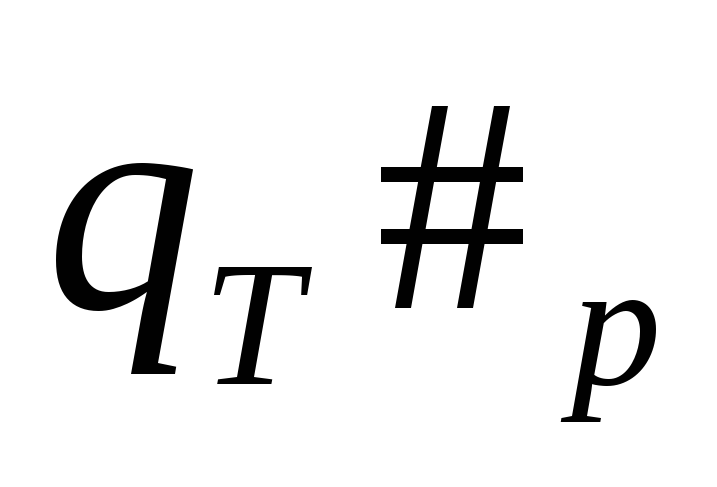
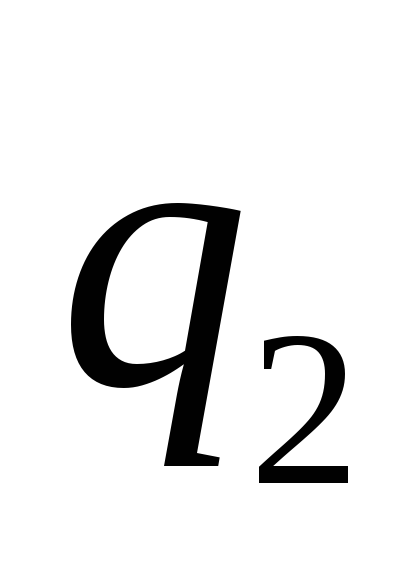
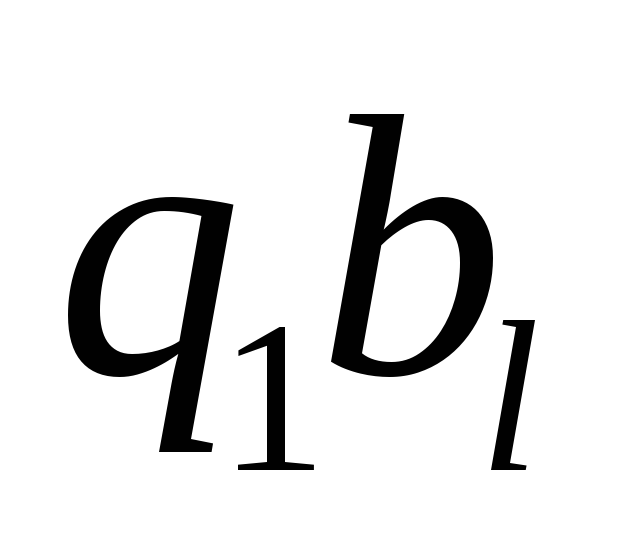
3. На ленте записана цепочка символов a и b. Необходимо всю цепочку заменить на , если количество символов четно, и на, если нечетно.

	a	b	#

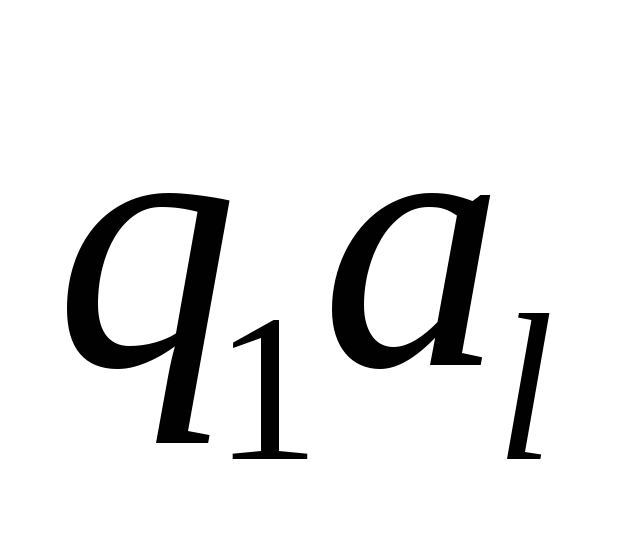
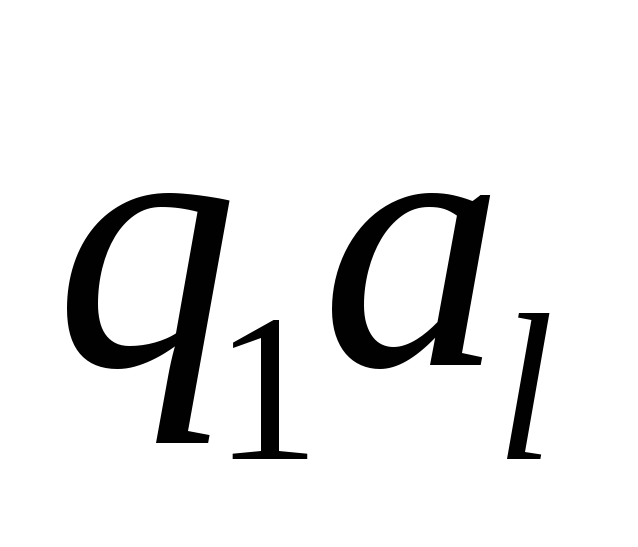
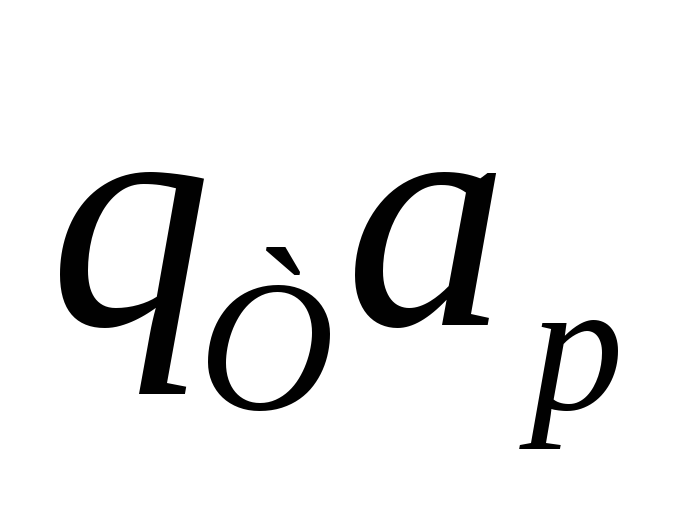
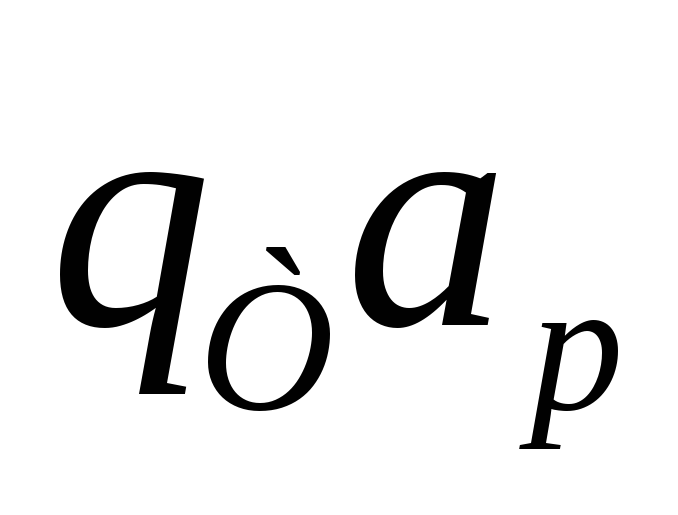
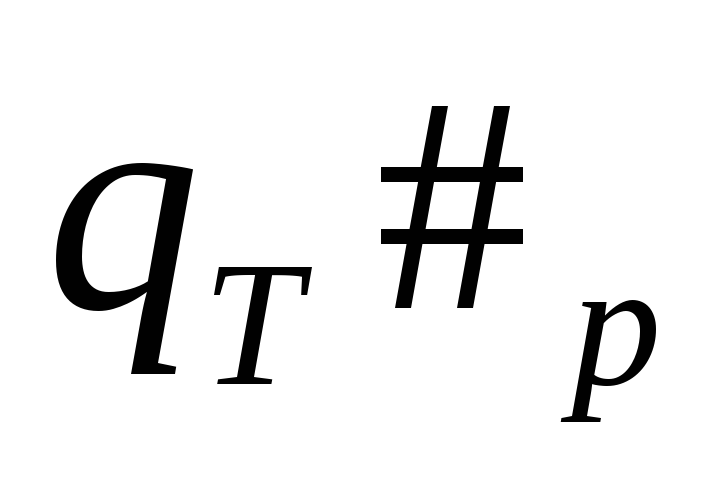
4. На ленте записано натуральное число в троичной системе счисления. Увеличить это число на 1.

	0	1	2	#

5.На ленте записано число в троичной системе счисления. Необходимо удвоить это число.

	0	1	2	#