Лекции и практики / tvps2

Неоднозначность грамматики

Грамматика называется неоднозначной, если существует цепочка соответствующего языка, определяемого грамматикой, которая выводима не менее чем двумя способами с точностью до порядка применения правил.

Две грамматики и эквивалентны, если они определяют один и тот же язык, т.е. совпадает с .

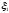Если правила грамматики имеют следующий вид: , где и ,и не пустые одновременно, где - пустая строка, то говорят о контекстно-зависимой грамматике. Контекстно-зависимые грамматики являются неукорачивающими, причём можно показать, что всякую неукорачивающую грамматику можно преобразовать в контекстно-зависимую грамматику, эквивалентную исходной. Класс языков, определяемых контекстно-зависимыми грамматиками, совпадает с классом языков 1. 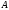Здесь и называются контекстом и замена на осуществляется в контексте.

Пример:

Рассмотренная ранее грамматика является неукорачивающей, и все правила, кроме четвёртого (), удовлетворяют требованиям контекстно-зависимой грамматики. Преобразуем это правило следующим образом:

4.1.

4.2.

4.3.

Помимо этого добавим правило , где М – двойник символа .

Грамматика называется контекстно-свободной (бесконтекстной), если все правила в ней имеют вид: , где А – нетерминальный символ, – непустая цепочка. Такие грамматики определяют языки класса 2. Данный класс является наиболее распространённым.

Пример контекстно-свободной грамматики:

1. SaSb

2. Sab

L={aⁿbⁿ | n = 1,2,3…} (данная грамматика определяет язык)

Укорачивающие контекстно-свободные грамматики

В укорачивающей контекстно-свободной грамматике любое правило имеет вид , но при этом может быть пустой цепочкой.

Автоматные грамматики

Для данных грамматик правила имеют вид: , где A и В – нетерминальные, а – терминальный символ.

Грамматики этого вида образуют языки класса 3. Для введённых классов языков справедливо включение класса i в класс (i-1).

Задача разбора

Задача разбора или распознавания заключается в том, что по данной грамматике G и цепочке Х требуется восстановить (построить) вывод этой цепочки или показать, что цепочка Х не принадлежит языку .

Автомат или устройство, которое решает задачу разбора, называется синтаксическим анализатором.

Определение: Цепочка редуцируется (свёртывается) непосредственно в цепочку , если в грамматике G существует правило: .

Определение: Цепочка редуцируется (свёртывается) в цепочку , , если существует последовательность цепочек такая, что и .

Задача разбора, вообще говоря, противоположна задаче порождения. В задаче разбора идёт восстановление вывода цепочек, т.е. имеется редуцируемость . Поэтому иногда говорят о свёртке.

Нормальные формы Бэкуса-Наура.

Б.Н.Ф. – нотация

При определении многих языков программирования используется Б.Н.Ф. – нотация. Она позволяет, в частности, записывать выражения, которые определяют множество последовательностей символов (т.е. формальный язык). Данные выражения называют также регулярными выражениями.

Пример: Десятичная запись целых чисел как регулярное выражение.

Множество целых чисел без незначащих нулей может быть записано следующим образом:

0|[{-}[1|2|3|4|5|6|7|8|9{1|2|3|4|5|6|7|8|9|0}*]]

Словесно эта запись может быть проинтерпретирована так: целые числа в десятичной системе счисления представляются символом “0” или последовательностью символов, которая может начинаться символом “-” или он может быть опущен, а далее следует отличная от нуля цифра, вслед за которой может следовать любая (конечная) последовательность цифр.

Пусть С – множество символов, называемых терминальными символами. Регулярные выражения над множеством символов С определяют формальный язык, т.е. некоторое подмножество из С*.

Перечислим отдельные элементы регулярных выражений и их значение:

1. Терминальные символы.

Пусть . Тогда с – есть регулярное выражение с языком [c].

2. Объединение.

Пусть R и Q – регулярные выражения с языками X и Y. Тогда R|Q обозначает регулярное выражение с языком .

3. Конкатенация.

Пусть R и Q – регулярные выражения с языками X и Y. Тогда RQ означает регулярные выражения с языком

а) Опция.

{R} - регулярное выражение с языком

б) Итерация.

{R}* - регулярное выражение с языком

в) Итерация.

{R}⁺ - регулярное выражение с языком

г) - регулярное выражение определяет язык Х.

д) - определяет регулярное выражение с языком .

Б.Н.Ф.-нотация допускает введение обозначений для формальных языков. Пусть имеется множество обозначений и h – произвольное обозначение, а R – регулярное выражение. Чтобы отличать обозначение от произвольной цепочки, будем брать обозначение в условные скобки - синтаксическая единица.

С помощью Б.Н.Ф.-правила ::=R принимается соглашение, что синтаксическая единица обозначает формальный язык, который описывается с помощью регулярного выражения R. В данном выражении символы, которые записываются в , называются нетерминальными, а символы, принадлежащие С, – терминальными.

Используя нетерминальные символы, можно обозначить сокращения для терминальных выражений, т.е. регулярные выражения могут содержать синтаксические единицы, т.е. их запись стоит вместо записи некоторого формального языка.

Пример: Десятичная система записи целых чисел.

В этом примере синтаксические единицы применяются для сокращения регулярного выражения. Если мы вместо них подставим соответствующие регулярные выражения, то синтаксические единицы могут быть ликвидированы. Однако в общем случае синтаксические выражения убрать нельзя. Это свойство возникает, если имеется Б.Н.Ф.-правило , в котором регулярное выражение R содержит синтаксическую единицу е, стоящую в левой части. В этом случае говорят о рекурсивном Б.Н.Ф.-правиле.

Рекурсивные Б.Н.Ф.-правила позволяют описывать определённые формальные языки, которые не могут быть представлены с помощью регулярных выражений. Такими языками являются, например, языки, допускающие вложенные структуры.

Пример: Арифметическое выражение в Б.Н.Ф.

Язык арифметических выражений над целыми числами с операциями умножения, сложения и вычитания определяют формальный язык над символами 0,1,2,3,4,5,6,7,8,9,(,),-,+, *.

::= | () | [+ | - | *]

::={[{ | 0}*]}

::=[1|2|3|4|5|6|7|8|9]

5