Определение основных размеров эм

Внутренний диаметр сектора

.

Постоянные величины сектора:

,

,

.

Координаты максимума :

.

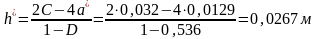Приближенные значения ширины окна под обмотку

,

.

Ширина полюса

Толщина полюсов

_{Плечо приложения силы ЭМ}

.

Начальное значение высоты окна под обмотку

.

Средний диаметр зубцовой зоны

.

_{Перемещение якоря ЭМ при перемещении зубца ГЯ на расстояние}

.

Начальный немагнитный зазор якоря ЭМ

Высота электромагнита

Величина

Площадь окна под обмотку

.

Площадь поперечного сечения стали магнитопровода

где при толщине пластины стали

Величина прямо пропорциональная изгибающему моменту:

Электромагнитный расчет ЭМ

Перегрев обмотки при расчетной температуре

.

Боковая поверхность обмотки

Величина находиться в интервале , поэтому , с учетом таблицы 1.2.1. коэффициент теплоотдачи при

,

При расчетной температуре

.

Сила тока обмотки

;

т.к. в фазе ТВШД два последовательно соединенных ЭМ, то напряжение на обмотке одного ЭМ .

Сопротивление обмотки при

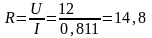
Удельное электрическое сопротивление меди при

.

Средняя длина витки обмотки

_{Начальное значение сечения провода по меди}

.

Выбрав медный обмоточный провод с высокопрочной двухслойной эмалевый изоляцией марки ПЭВ-2, по приложению 1 определяют: , , .

Начальной значение коэффициента заполнения окна медью

,

_где - коэффициент укладки.

_{Сеченение провода по меди при первом приближении}

_{По приложению 1:} , .

Коэффициент заполнения окна медью

;

, то окончательно принимаются значения провода при первом приближении и находится плотность тока

.

_{Далее определяются:}

_{число витков обмотки}

;

_{МДС обмотки}

;

Изгибающий момент ЭМ без учета магнитного насыщения стали и потока рассеяния

;

Начальное значение магнитной индукции в воздушном зазоре

.

С учетом насыщения стали и магнитного потока рассеяния магнитную индукцию в воздушном зазоре выберем меньше , например, и рассчитаем магнитную цепь ЭМ.

Магнитный поток в воздушном зазоре

.

Магнитный поток рассеяния ЭМ через окно

.

Магнитный поток в сердечнике ЭМ

.

_{Напряженность магнитного поля в воздушном зазоре}

.

Напряженность магнитного поля в якоре при 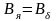для листовой электротехнической стали толщиной марки Э-12 определяют по кривой намагничивания (Приложение 2) и составляет .

Магнитная индукция в сердечнике

Напряженность магнитного поля в сердечнике при определяют по кривой намагничивания стали Э-12 и составляет .

Средние длины участков магнитопровода ЭМ – сердечника и якоря:

,

.

МДС, необходимая для создания выбранного значения

_{МДС из расчета заданного перегрева обмотки IW=1278А.}

Обе МДС почти равны, поэтому выбрано правильно.

Тяговое усилие ЭМ при начальном воздушном зазоре

.

Изгибающий момент

.

Аналогичные расчеты выполнены для других значений . Значения изгибающих моментов и высот ЭМ приведены в Табл. П3.1.

Таблица П3.1. Изгибающие моменты и высоты ЭМ.

	8,6	10	11	8,6	3,5
	0,066	0,09	0,1	0,11	0,13
	0,091	0,115	0,125	0,135	0,155

Из табл. П3.1. видно, что наибольший изгибающий момент 11 при высотах окна и электромагнита . Оптимальное значение больше начального значения в 1,5 раз. Поэтому точек наибольшего значения М можно проводить также следующим образом – расчет ЭМ проводят при предполагаемом оптимальном значении , а также при уменьшенных и увеличенных значениях его.

Некоторые электромагнитные и обмоточные данные ЭМ с наибольшим изгибающим моментом и начальным немагнитным зазором приведены в табл. П3.2.

_{Таблица П3.2. Электромагнитные и обмоточные данные оптимального ЭМ}

12	1,19	10,08				1578	0,85	1,57	0,85

_{Другие размеры и величины этого же ЭМ приведены в табл. П3.3.}

_{Таблица П3.3. Другие размеры и величины оптимального ЭМ.}

0,0142	0,0374	0,012	0,0236	0,0707	0,034	0,045	0,032	0,536	1,417·10-3	2,718·10-4	38,584·10-12

Проведем также расчетное исследование, показывающее на сколько процентов отличаются предполагаемые величины и , доставляющие максимум функции от действительных и . Результаты этого исследования показаны в таблице П3.4.

Таблица П3.4. Поиск , _, .

	0,0142	0,015	0,016
	38,584	38,965	38,502
	0,014	0,015	0,016
	38,686	39,117	38,58
	0,014	0,015	0,016
	38,891	39,271	38,607
	0,014	0,015	0,016
	39,022	39,299	38,483
	0,014	0,015	0,016
	39,053	39,193	38,239

Из табл. П3.4. видно, что , , и соответственно отличаются от значений , , т.е. отличие небольшое и предлагаемое определяемое , в начале расчета оправдано.

Ниже приведено определение тягового усилия ЭМ при конечном немагнитном зазоре , когда зубец ГЯ переместится вниз на расстояние .

Электрические и обмоточные данные соответствуют оптимальному ЭМ с (табл. П3.2.).

МДС обмотки

.

Значение выберем несколько большее, чем в табл. П3.2. из-за меньшего воздушного зазора, например, .

Магнитный поток в воздушном зазоре

Магнитный поток рассеяния ЭМ через окно

Магнитный поток в сердечнике ЭМ

Напряженность магнитного поля в воздушном зазоре

Напряженность магнитного поля в якоре при по кривой намагничивания

стали(Приложение 2) .

Магнитная индукция в сердечнике

Напряженность магнитного поля в сердечнике по кривой намагничивания

МДС по расчету магнитной цепи

;

и близки по значениям, поэтому значение можно не корректировать.

Тяговое усилие ЭМ при

.

Изгибающий момент

Индуктивность обмотки и электромагнитная постоянная времени при :

,

,

.

Индуктивность обмотки и электромагнитная постоянная времени при :

,

,

;

Время такта

.

Период следования импульсов напряжения(тока):

при шеститактной коммутации

;

при восьмитактной коммутации

;

при четырехтактной коммутации

.

Момент и мощность на валу ТВШД

Средний диаметр зубцовой зоны

.

Число зубцов Ж. В.

,

Число зубцов ГЯ

Угловая скорость перемещения волны деформации

угловая скорость вала

Передаточное отношение

частота вращения вала

.

время полного оборота

Результирующая электромагнитная сила на каждом такте коммутации

Результирующая электромагнитная сила в зубцовой зоне

Момент на валу

Мощность на валу

_{Расчет зависимостей i(t), u(t), p(t).}

_{Результаты расчетов вышеуказынных зависимостей сводят в табл. П3.5.}

_{Табл. П.3.5. Мгновенные значения i, F, n, p.}

	, Н	, м	, А	, В	, Гн	, А	, с	, с	, В	, В	, В	, В	, ВА
a’	0	1·10-3	0	0	0,425	0,65	0	0,042	2,682	0,206	0	2,682	0
b’	1,082·102	0,69·10-3	0,53	5,34	0,837	0,595	0,084	0,084	5,929	0,089	0,562	11,831	6,27
c’	1,95·102	0,43·10-3	1,19	12	0,602	0,33	0,168	0,126	1,577	0,1175	1,110	14,687	17,48
d’	2,164·102	0,2·10-3	1,19	12	0,62	0	0,336	0,168	0	0,018	0,127	12,127	14,43
e’	1,95·102	0,43·10-3	1,19	12	0,602	-0,33	0,504	0,126	-1,577	-0,1175	-1,110	9,313	11,082
e’	1,082·102	0,69·10-3	0,53	5,34	0,837	-0,595	0,588	0,084	-5,929	-0,089	-0,562	-1,151	-0,61
q’	0	1·10-3	0	0	0,425	-0,265	0,672	0,042	-2,682	=0,206	0	-2,682	0

Вначале, для указанных положений якоря ЭМ, определяют величины первых пяти столбцов табл. П3.5.

Положение якоря ЭМ в т.

этому положению соответствует расчет ЭМ при воздушном зазоре и : Результаты расчет , .

Положение якоря ЭМ в т. и

Определение тягового усилия и индуктивности ЭМ при проводятся также, как при конечном воздушном зазоре и той

же величине МДС, поэтому расчет приводится без пояснения.

,

что близко к 1878А

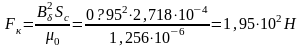
Положение якоря ЭМ в т. и

.

Положение якоря ЭМ в т. и

Затем определяют приращение тока , времени , индуктивности , величины напряжений и общее напряжение и как алгебраическую сумму их.

Расчетные зависимости.

Зависимость F(t) показана на рис. 2.2.4 сплошной линией и близка к требуемой трапецеидальной зависимости; величины F соответствуют таблице П.3.5. в точках значения электромагнитных сил меньше силы в т. на 99%.

На рис. П.3.1 построены зависимости тока i(t), напряжения u(t) и мгновенной мощности P(t) по таблице П.3.5; по горизонтальной оси время кратно времени такта . На этом же рис. Показаны также средние значения мощности Р_ср, потребляемые электромагнитами зоны на такте коммутации, а также зависимости i²(t) для определения мощности потерь в обмотках – .

Как видно из рис. П.3.1 требуемая, из условия постоянства мгновенной угловой скорости перемещения волны деформации, форма импульса напряжения u(t) существенно отличается от однополярного импульса u_п(t).