Р. А. Хуснутдинов, Е. И. Цокур

РАСЧЕТ ТОРЦОВОГО ВОЛНОВОГО ШАГОВОГО ДВИГАТЕЛЯ

Казань 2016

Министерство образования и науки Российской Федерации

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

«КАЗАНСКИЙ НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

им. А. Н. ТУПОЛЕВА – КАИ»

Р. А. ХУСНУТДИНОВ, Е. И. ЦОКУР

РАССЧЕТ ТОРЦОВОГО ВОЛНОВОГО ШАГОВОГО ДВИГАТЕЛЯ

Учебное пособие

Рекомендовано к изданию отделом методического

сопровождения учебного процесса

КНИТУ-КАИ

Казань 2016

УДК 621.313.13 (075.8)

ББК 3 261.2Я7

Ху 98

Рецензенты:

Кафедра электропривода и электротехники Казанского национального исследовательского технологичсекого университета; доктор технических наук, профессор В. Ю. Корнилов (Казанский государственный энергитечский университет)

Хуснутдинов Р. А.

Ху 98 Расчет торцового волнового шагового двигателя: учебное пособие/ Р. А. Хуснутдинов, Е. И. Цокур. – Казань: Изд-во Казан.гос.техн. ун-та, 2016. – с.

ISBN 978-5-7579-1990-4

Учебное пособие предназначено для выполнения курсовой работы по дисциплине «Электрические машины» для студентов очного и залчного обучения по направлению 130302 «Энергетика и электротехника»

Табл.8. Ил.13. Библиогр.: 2 назв.

© Изд-во Казан.гос.техн. ун-та,2016

ISBN 978-5-7579-1990-4 © Р.А. Хуснутдинов, Е. И. Цокур, 2016

Введение

Одним из наиболее целесообразных способов улучшения параметров электрических приводных устройств является применение тихоходных электродвигателей, основанных на использовании волновых зубчатых передач с электромагнитным генератором волн деформации торцовых волновых шаговых двигателей (ТВШД).

Особенностями ТВШД являются: большое передаточное отношение в одной степени зубчатого зацепления, что обеспечивает низкие скорости и большие моменты; возможность использования в составе дискретных электроприводов с малыми люфтами, дискретного шага, статической погрешностью отработки единичных шагов; возможность выполнения пустотелого вала и др.

Рассмотрим ТВШД, принципиальная схема которого приведена на рис.13.1.

ТВШД имеет плоское гибкое колесо – гибкий якорь (ГЯ) 1, на наружной окружности которого находится зубчатый венец 2. Это колесо не вращается. Оно закреплено на корпусе 3 по внутренней окружности. С выходным валом двигателя связано жесткое колесо – жесткий венец (ЖВ) 4 с ответным зубчатым венцом 2.

Автономные П-образные магнитопроводы 5 с обмотками возбуждения (ОВ) 6, установленные на корпусе двигателя, расположены перпендикулярно ГЯ. В окнах гибкого неферромагнитного якоря закреплены раздельные накладные магнитопроводы (НМП) 7, которые отделены от П-образных магнитопроводов 5 двумя воздушными зазорами. При последовательном подключении электромагнитов (ЭМ), состоящих из ОВ 6 и П-образных магнитопроводов 5, к источнику постоянного тока происходит деформирование гибкого якоря 1 таким образом, что обеспечивается контакт зубьев в зубчатом зацеплении 2. В результате жесткий венец 4 дискретно поворачивается.

В приведенной конструкции ТВШД используется двухполюсные электромагниты (ЭМ) клапанного типа, состоящие из 5, 6, 7 и двух воздушных зазоров.

Расчет ТВШД состоит из двух частей: в первый части рассчитываются электромагниты генератора волн деформации гибкого якоря [1], во второй части с использованием передачи [2] рассчитываются энергетические характеристики ТВШД.

Задания на курсовую работу по дисциплине «Электрические машины»

Dн, м	КД	α, град
0,3	4	22,5
0,3	3	22,5
0,3	2	22,5
0,2	4	22,5
0,2	3	22,5
0,2	2	22,5
0,1	4	22,5
0,1	3	22,5
0,1	2	22,5
0,3	4	30
0,3	3	30
0,3	2	30
0,2	4	30
0,2	3	30
0,2	2	30
0,1	4	30
0,1	3	30
0,1	2	30
0,3	4	45
0,3	3	45
0,3	2	45
0,2	4	45
0,2	3	45
0,2	2	45
0,1	4	45
0,1	3	45
0,1	2	45

1. Расчет электромагнита (эм)

Решается задача расчета электромагнита, вписанного в сектор, развивающего максимальный момент деформации сектора гибкого якоря торцевого волнового шагового двигателя (ТВШД) при заданных величинах постоянного напряжения питания и перегрева обмотки.

1. Определение основных размеров ЭМ

Тяговое усилие двухполюсного электромагнита

(1.1.1)

где , Тл – магнитная индукция в воздушном зазоре, S_c, м² – площадь сечения магнитопровода, Гн/м – магнитная проницаемость воздуха.

Магнитный поток

Вб (1.1.2)

С учетом (1.1.2)

Н. (1.1.3)

Пренебрегая потоками рассеяния и падением магнитного напряжения в магнитопроводе можно записать, что

, Вб, (1.1.4)

где - сила тока в А и число витков обмотки;

Магнитное сопротивление воздушного зазора

, (1.1.5)

где , м – суммарный воздушный зазор.

С учетом (1.1.4), (1.1.5)

Н (1.1.6)

Сила тока в обмотке

А, (1.1.7)

где , - плотность тока, - сечение обмоточного привода без изоляции.

Число витков обмотки

(1.1.8)

где 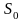, - площадь окна под обмотку; - коэффициент заполнения окна медью.

С учетом (1.1.7), (1.1.8)

Н (1.1.9)

и момент деформации (изгибающий момент)

(1.1.10)

где , м – плечо приложения силы F.

Из (1.1.10) видно, что момент прямо пропорционален . Рассмотрим подробнее эту величину.

На рис. 1.1.1 показаны размеры электромагнита, вписанного в сектор, образованный наружным диаметром D_н, внутренним диаметром D_вн и углом α.

Рис. 1.1.1 Размеры ЭМ

Из Рис. 1.1.1 можно записать, что:

Ширина полюса, м

, (1.1.11) где и , - наружный и внутренний диаметры сектора,

, и , - ширина окна под обмотку и расстояние от внутреннего диаметра сектора до обмотки;

толщина полюса,

, (1.1.12)

где - угол сектора;

высота окна под обмотку,

(1.1.13)

где ,

высота электромагнита,

, (1.1.14)

где , м – начальное значение немагнитного зазора между якорем ЭМ и сердечником.

Средний диаметр зубцовой зоны

, (1.1.15)

где - зазор по радиусу между наружным стержнем ЭМ и краем окна ГЯ, - выступ якоря, ЭМ для его крепления к ГЯ, - длина зубца (Рис. П3.2).

При перемещении зубца ГЯ на расстояние якорь ЭМ переместится на расстояние

. (1.1.16)

Начальный немагнитный зазор якоря ЭМ

. (1.1.17)

Плечо приложения силы,

(1.1.18)

площадь окна под обмотку

, (1.1.19)

площадь полюса

, (1.1.20)

где - коэффициент заполнения сердечника сталью.

Проанализируем как зависит от и

С увеличением и произведение увеличивается. С увеличением , второй сомножитель в уменьшается, а третий – увеличивается, следовательно при изменении имеет максимум; при , имеет максимум. Координаты , максимума определяются из уравнений частных производных:

, (1.1.21)

; (1.1.22)

, (1.1.23)

. (1.1.24)

При изменении и , также будет иметь максимум, но его координаты , . C учетом проведенных расчетных исследований, координаты максимума можно приближенно определить по формуле:

, (1.1.25)

_{, (1.1.26)}

_{где коэффициент} , .

С учетом найденных величин и , по вышеприведенным формулам определяют: (все размеры в системе СИ).