Лекции и практики / tvps6

Асинхронный процесс

Назовём асинхронным процессом четвёрку <S,F,I,R>, в которой S – непустое множество ситуаций, F – отношение непосредственного следования ситуаций, определённых на множестве S, . В множестве S выделены два подмножества.

Первое – это множество инициаторов (), т.е. таких ситуаций из S, для которых , то из того, что .

R – множество результантов, , т.е. таких ситуаций из S, для которых, есл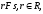и то и .

Отношение F является отношением непосредственного следования. Это означает, что если , то является причиной, а - возможным следствием. Инициаторы – это ситуации, активизирующие процесс, а результанты – это финальные ситуации.

Пусть имеется некоторая последовательность ситуаций s(1), …, s(i), s(i+1),… , где s(i) – элемент последовательности, стоящий на i-месте. Все последовательности, для которых выполняется s(i)Fs(i+1) для любого i кроме последнего, и ни одна последовательность не является частью другой, назовём допустимыми. Каждая допустимая последовательность ситуаций описывает возможный ход процесса смены ситуаций или траекторию асинхронного процесса. Мы можем построить отношение М, являющееся транзитивным замыканием отношения F, т.е. s_i M s_j, если существует траектория из s_i в s_j.

Асинхронный процесс будем называть эффективным, если он удовлетворяет следующим свойствам:

1. .

2. .

3. .

Таким образом, из инициаторов эффективного процесса все траектории ведут в результанты (свойства 1 и 3) и каждая из траекторий, приводящих к результантам, начинается в каком-либо инициаторе (свойства 1 и 2).

Эффективность асинхронного процесса оставляет место недетерминированности, т.е. возможно, что из некоторых инициаторов процесс попадает в различные результанты, однако он не содержит циклов вне ситуаций из множества R.

Введём на множестве ситуаций S отношение Е следующим образом:

1);

2) ;

3) .

Отношение Е – отношение эквивалентности. Оно позволяет разбить множество S на классы эквивалентности.

.

Для классов эквивалентности определим отношение F непосредственного следования:

Все допустимые последовательности классов эквивалентности, определённые отношением F, конечны. В них можно выделить начальные и конечные элементы, которые будем называть начальными и заключительными классами эквивалентности.

1. Если некоторая ситуация s является инициатором и , где S(j) – класс эквивалентности, стоящий на j-месте в некоторой допустимой последовательности, то все ситуации классов S(1), S(2) ,…, S(j), в этой последовательности являются инициаторами.

Доказательство:

Предположим противное:

Существует некоторая ситуация 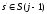, что Пусть согласно отношению F , где , причём не является инициатором (). Тогда согласно определению отношения Е мы имеем, что 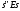, но согласно определению отношения F это означает, что s не должно быть инициатором. Таким образом, все состояния класса S(j) являются инициаторами и, кроме того, ситуация также является инициатором. Аналогично, уменьшая номер класса эквивалентности с помощью подобных рассуждений, полностью доказывается всё утверждение.

2. Если некоторая ситуация s является результантом и , то все ситуации из классов S(j), S(j+1) ,…, S(q), где S(q) – заключительный класс, являются результантами.

Доказательство: от противного - самостоятельно.

3. Для эффективного асинхронного процесса любой начальный класс состоит только из инициаторов, а любой заключительный – только из результантов.

Доказательство: самостоятельно.

4. Для эффективного асинхронного процесса любой класс эквивалентности ситуаций, не принадлежащий к результантам, состоит из одной ситуации.

Доказательство: самостоятельно.

Если в эффективном асинхронном процессе каждая допустимая последовательность классов ведёт из начального класса в один и только один заключительный класс, то такой процесс называется управляемым.

Таким образом, в управляемом асинхронном процессе вводится ограничение на степень недетерминизма: для каждого инициатора все начинающиеся в нём траектории ведут в один и тот же заключительный класс.

Если ситуации s_i и s_k некоторого асинхронного процесса связаны отношением , то фрагмент процесса, содержащий все части траектории, ведущей из , называется переходом .

Эффективный асинхронный процесс называется простым, если:

1) .

2) .

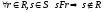Это означает, что из инициатора нельзя попасть в другой инициатор, а из результанта – в другой результант, следовательно, каждая траектория содержит в точности по одному инициатору и одному результанту.

Протоколом простого асинхронного процесса будем называть отношение . Из определения следует, что протокол асинхронного процесса задаётся лишь начальной и конечной ситуациями. Фактически, протокол простого асинхронного процесса можно рассматривать как простой асинхронный процесс, в котором за каждым инициатором непосредственно следует результант. Поэтому здесь множество ситуаций состоит лишь из инициаторов и результантов. При переходе от простого асинхронного процесса к его протоколу для каждой пары (i,r) пучки траекторий, ведущие из i в r, заменяются одной дугой. Протокол является удобной формой “входно-выходного” описания исходного процесса.

До сих пор ничего не говорилось о механизмах перехода от результантов к инициаторам. Описание подобного механизма необходимо для получения эффекта возобновления асинхронного процесса и его повторных активизаций. Такой механизм задаётся репозицией асинхронного процесса.

Репозицией асинхронного процесса P=<S,F,I,R> называется эффективный асинхронный процесс P’=<S’,F’,I’,R’> такой, что множество ситуаций .

Ситуации S’ репозиции могут содержать лишь те ситуации из исходного процесса, которые являются лишь инициаторами или результантами и, кроме того, некоторые дополнительные ситуации S^д, отсутствующие в описании исходного асинхронного процесса, т.е. Ш.

Отношение F’ задаёт траектории переходов от элементов из I’ (первоначальных результантов исходного асинхронного процесса) к элементам из R’. При этом переходы, возможно, осуществляются через дополнительные ситуации из S^д. Если мы имеем, что I’=R, а R’=I, то репозиция называется полной. Если отношение F’=Ш, то репозиция не существует. Во всех остальных случаях репозиция называется частичной. Объединение асинхронного процесса и его полной репозиции образует автономный процесс P^а=<S^а, F^а>, где S^а – ситуации автономного процесса: , . В автономном процессе не выделяются множества I и R, поэтому траектории переходов могут быть бесконечны.

Полные репозиции простого и непростого асинхронных процессов будем называть соответственно тривиальной и нетривиальной. При нетривиальной репозиции в качестве инициаторов асинхронного процесса репозиции могут выступать результанты исходного асинхронного процесса, необязательно принадлежащие заключительному классу эквивалентности.

Обозначим R^з – объединение заключительных классов эквивалентности ситуаций некоторого асинхронного процесса. S^t обозначим множество ситуаций асинхронного процесса, принадлежащих траектории t.

Пусть задан управляемый асинхронный процесс P=<S,F,I,R> такой, что:

1. Каждый его заключительный класс эквивалентности состоит из одного результанта.

2. Вместе с нетривиальной репозицией асинхронный процесс образует автономный процесс P^а=<S^а, F^а> на множестве ситуаций S^a. На этом множестве определена функция такая, что если в исходном управляемом асинхронном процессе справедливо отношение iMr (), то в соответствующем автономном процессе из того, что 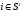следует, что существует ситуация такая, что iM^as и кроме того g(s)=r.

Автономный асинхронный процесс, удовлетворяющий свойствам 1 и 2 и имеющий фрагменты траектории вида , где g(s₁)=r, g(s₂)=r, называется конвейерным асинхронным процессом.

Введение понятия конвейерного асинхронного процесса позволяет изучать конвейерный принцип обработки информации. В его основе лежит идея такой повторной инициации асинхронного процесса, при которой асинхронный процесс ещё не достиг результанта из заключительного класса эквивалентности ситуаций.

Здесь может быть такая аналогия: имеется наклонный жёлоб, по которому скатываются шарики. Когда запущен первый шарик, на верхний конец жёлоба можно поместить второй шарик, потом третий и т.д. Очередной шарик может догнать предыдущий или отстать от него, но не может обогнать. Догнав, он может катиться дальше не быстрее предыдущего.

Для описания процессов и задания их взаимодействия часто требуется структурировать ситуации. Структурирование, в зависимости от решаемых задач, может выполняться различными способами. Один из способов – разбиение ситуаций на компоненты (события). При этом каждой компоненте ставится в соответствие некоторая логическая переменная p_i (p_i=1, если значение, соответствующее логическому условию, истинно и p_i=0 в противном случае). При таком структурировании ситуация представляется двоичным вектором. Размерность вектора равна числу семантически задаваемых компонентов. Значению 1 соответствует число истинных (в данной ситуации) логических переменных. Попытки применить асинхронный процесс в приложениях обязательно связаны с семантической интерпретацией и структурированием ситуаций.

Асинхронный процесс является общей моделью описания динамики поведения параллельно функционирующих асинхронных систем. Каждой такой последовательности соответствует некоторая траектория асинхронного процесса. В этом смысле можно говорить о том, что асинхронный процесс есть модель управляющей структуры системы.

Асинхронный процесс может служить инструментом исследования весьма общих свойств и закономерностей параллельных систем, абстрагирующимся от семантики их работы. Поэтому асинхронный процесс можно считать неинтерпретируемой моделью. С другой стороны, асинхронный процесс можно понимать как метамодель, порождающую различные, широко используемые динамические модели. Порождение частных моделей предусматривает использование механизма интерпретации асинхронных процессов, который может быть двухступенчатым:

I этап: Модельная интерпретация – состоит в том, что основным понятиям асинхронного процесса ставятся в соответствие понятия частных моделей. Эта система соответствий базируется на введении дополнительных ограничений на асинхронный процесс.

II этап: Модельная интерпретация сама по себе может оставаться неинтерпретированной моделью. Однако, если асинхронному процессу или его модельным интерпретациям при решении конкретных задач поставить в соответствие некоторые метки, то такие модели становятся интерпретированными. При этом метки должны обозначать символы, операторы, атрибуты или логические переменные, которые задаются из семантических соображений конкретного объекта. Этот процесс является предметной интерпретацией асинхронного процесса. Такая интерпретация должна быть согласована с приложениями и зависеть от специфики решаемых задач.

6