Машина Тьюринга

Для машины Тьюринга предусмотрено помимо чтения символов с входа еще и их изменение во входной цепочке.

За один такт работы машины Тьюринга происходит изменение считанного машиной Тьюринга символа и переход к считыванию следующего символа, который может располагаться либо там же, где находится считанный в текущем такте, либо непосредственно левее или правее. При этом также происходит изменение состояния.

Машина Тьюринга была придумана как механизм формализации понятия алгоритма. Правило функционирования машины Тьюринга удобно задавать в виде таблицы. В левом столбце находятся состояния машины Тьюринга, верхняя строка соответствует символам входного алфавита. На пересечении строки и столбца записывается тройка, указывающая, в какое следующее состояние переходит машина Тьюринга, какой символ записывается вместо считанного, и откуда считывается следующий символ цепочки (l,p,r).

Т.к. цепочка считается бесконечной в обе стороны (конечная цепочка дополняется специальными пустыми символами), то специально выделяется набор терминальных состояний. Первоначально считывающая головка находится над самым левым непустым символом.

Возможны несколько модификаций машины Тьюринга, определяющих результаты её работы:

1) результатом работы считается цепочка, получившаяся из исходной в результате изменений, произведённых машиной Тьюринга. В этом случае обычно вводится только одно терминальное состояние.

2) предполагает, что результатом работы машины Тьюринга является её состояние, в котором она прекращает функционирование (одно из нескольких терминальных состояний).

3) использование нескольких входных цепочек с выходными символами, заносимыми в отдельную (не совпадающую со входной) цепочку.

4) другие.

Минимизация конечного автомата

Автоматы являются моделями устройств для переработки дискретной информации. Входной и выходной алфавиты автоматов зависят только от решаемой задачи. На внутренний алфавит Q (множество состояний автомата) обычно никаких ограничений не накладывается. Поскольку преобразование информации может быть осуществлено автоматами с различным числом состояний, возникает задача построения автомата с минимальным числом состояний. Рассмотрим сначала случай всюду определённых автоматов.

Состояния q автомата M и q’ автомата M’ называются эквивалентными, если оба автомата, получив одну и ту же последовательность входных символов, находящихся в состояниях q и q’ соответственно, перерабатывают её в одинаковую последовательность выходных символов. Если M и M’ – один и тот же автомат, то мы имеем эквивалентные состояния для одного автомата. Автоматы M и M’ будем называть эквивалентными, если для каждого состояния автомата М существует эквивалентное состояние автомата М’ и наоборот. На частичные автоматы понятие эквивалентности не распространяется. Это связано с тем, что выходные последовательности могут допускать различные доопределения, а это приводит к неэквивалентным автоматам. Однако для частичных автоматов может быть введён некоторый аналог понятия эквивалентности.

Пусть и- последовательности, составленные из символов некоторого алфавита и неопределённого символа “-”. Будем говорить, что последовательность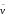покрывает последовательность, если некоторые неопределённые символы последовательностиможно заменить так, что получится.

Например: =2 - 102 - -1

=2 - -02 - -1

Последовательность x₁,x₂,…,x_p символов входного алфавита V применима к состоянию q частичного автомата М, если определены состояния q₁=ψ(x₁q), q₂=ψ(x₂q₁),…, q_p=ψ(x_p,q_p-1), где ψ(x,q) – функция перехода.

Будем говорить, что состояние q’ частичного автомата M’ покрывает состояние q частичного автомата М, если:

1. Любая последовательность входных символов, применимая к состоянию q автомата М, применима и к состоянию q’ автомата M’.

2. Соответствующая последовательность выходных символов автомата М’ покрывает последовательность выходных символов автомата М.

Если для каждого состояния q автомата M найдётся покрывающее его состояние q’ автомата M’, то говорят, что автомат M’ покрывает автомат М.

Автомат, покрывающий М и имеющий наименьшее число состояний, будем называть минимальным автоматом для М.

Задача минимизации автоматов решается в несколько этапов:

1. Нахождение эквивалентных состояний

Рассмотрим множество Q всех состояний некоторого всюду определенного автомата М. Отношение эквивалентности состояний обладает свойствами транзитивности, симметричности и рефлексивности. Поэтому множество Q разбивается на классы эквивалентности.

Рассмотрим метод нахождения пар (q_i, q_j) эквивалентных состояний. Применение этого метода рассмотрим на примере автомата, заданного таблицей:

q\x	0	1	2
q1	q4, 1	q6, 0	q1, 0
q2	q2, 0	q2, 0	q6, 1
q3	q4, 1	q2, 0	q3, 0
q4	q4, 1	q3, 0	q3, 0
q5	q6, 0	q6, 0	q5, 1
q6	q5, 0	q6, 0	q2, 1

Составим треугольную таблицу, клетки которой соответствуют всем различным неупорядоченным парам состояний (q_i, q_j) для .

Заполним её следующим образом: если для состояний q_i и q_j существует входной символ х, приводящий к различным значениям выхода, то соответствующую клетку таблицы перечеркнём. Если же для каждого х выход автомата в состоянии q_i и в состоянии q_j принимает одинаковые значения, то в клетку, соответствующую этой паре, записываем все пары состояний (q_v, q_w), , отличные от пары (q_i, q_j), в которые автомат может перейти при подаче одного и того же входного символа.

q2

q3

q6q2

q4

q1 q3 q6 q3

q2 q3

q5

q2 q6 q5 q6

q6

q2 q5

q2 q5

q1

q2

q3

q4

q5

Далее в таблице необходимо зачеркнуть клетки, в которых содержатся пары состояний, соответствующих вычеркнутым клеткам. Процесс продолжать до тех пор, пока не получится таблица, в которой ни одной клетки вычеркнуть нельзя. Невычеркнутые клетки результирующей таблицы соответствуют всем парам эквивалентных состояний.

q2

q3

q6q2

q4

q1 q3 q6 q3

q2 q3

q5

q2 q6 q5 q6

q6

q2 q5

q2 q5

q1

q2

q3

q4

q5

Пусть состояния q’ и q’’ неэквивалентны. Это означает, что найдётся последовательность входных символов =х₁,х₂,…,х_р, на которых автомат, запущенный с состояний q’ и q’’, выдаёт различные последовательности. Можно считать, что выходы различаются лишь на шаге р, т.е. после подачи на вход символа х_р. Пусть, начав из состояния q’, автомат проходит последовательность состояний , а начав из состоянияq^’’, проходит последовательность . В состоянияхподача на вход символа х_р приводит к разным значениям выхода. Следовательно, пара будет вычеркнута из треугольной таблицы на первом шаге при её начальном заполнении.

Поскольку символ х_р-1 сопоставляет паре пару состояний, то на следующем шаге изменения треугольной таблицы паратакже будет вычеркнута и т.д. и не позже, чем через р шагов, исходная параq’, q’’ будет вычеркнута. Если же состояния q’ и q’’ эквивалентны, то всякой входной последовательности будут соответствовать одинаковые выходные последовательности и не найдётся пара состояний, исходя из которой цепочка вычёркиваний клеток треугольной таблицы приведёт к q’ и q’’.

На основе итоговой треугольной таблицы выпишем все пары эквивалентных состояний: (q₁q₃), (q₂q₅), (q₂q₆), (q₅q₆). Класс эквивалентности образуется состояниями, которые попарно эквивалентны. В нашем случае мы получаем классы {q_1,q₃},{q_2,q_5,q₆},{q₄}. Каждое состояние, не вошедшее ни в один из классов, эквивалентно лишь себе, и само образует класс эквивалентности. Таким образом, в рассмотренном примере найдено 3 класса эквивалентности состояний.

2. Построение минимального автомата

Пусть имеется некоторое разбиение всех состояний автомата М на множества Q_1,Q_{2, … ,}Q_S. Разбиение V назовём замкнутым, если для любого множества Q_v и любого входного символа х, множество всех состояний, в которые под действием х автомат переходит из состояния q_v в Q_v, целиком содержится в некотором множестве Q_w (зависящем от х и v). Покажем, что разбиение множества состояний на классы эквивалентности является замкнутым.

Действительно, если состояния q_i и q_j эквивалентны, и при подаче на вход символа х они переходят в состояния , то последние также будут эквивалентными состояниями. Таким образом, состояния из одного класса эквивалентности при подаче одного и того же входного символа снова попадают в один класс эквивалентности. Это доказывает замкнутость разбиений.

Имея разбиение множества состояний М на классы эквивалентности Q_1,Q_2,…,Q_S, построим новый автомат М^’. Для этого каждому классу эквивалентности Q_i сопоставим состояния q^‘_i (i=1,2,…,s). В качестве входного и выходного алфавитов автомата М^’ возьмём алфавиты автомата М. Чтобы назначить переход в автомате М^’ из состояния при входном символе х, рассмотрим соответствующий класс эквивалентностиQ_v. Согласно свойству замкнутости символ х переводит все состояния из Q_v в Q_w. Им определяется . По свойству эквивалентности состояний, подача входного символа х в каждом состоянии изQ_v приводит к одинаковому значению выхода. 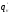Оно принимается в качестве выходного значения, соответствующего переходу в автомате M^’ из под действием х.