4.2. Графический способ определения усилий.

Этот способ основан на правилах векторной математики, способах построения векторных многоугольников. Построение диаграммы Максвелла - Кремоны заключается в соединении силовых многоугольников, построенных для всех узлов фермы согласно условию равновесия узлов.

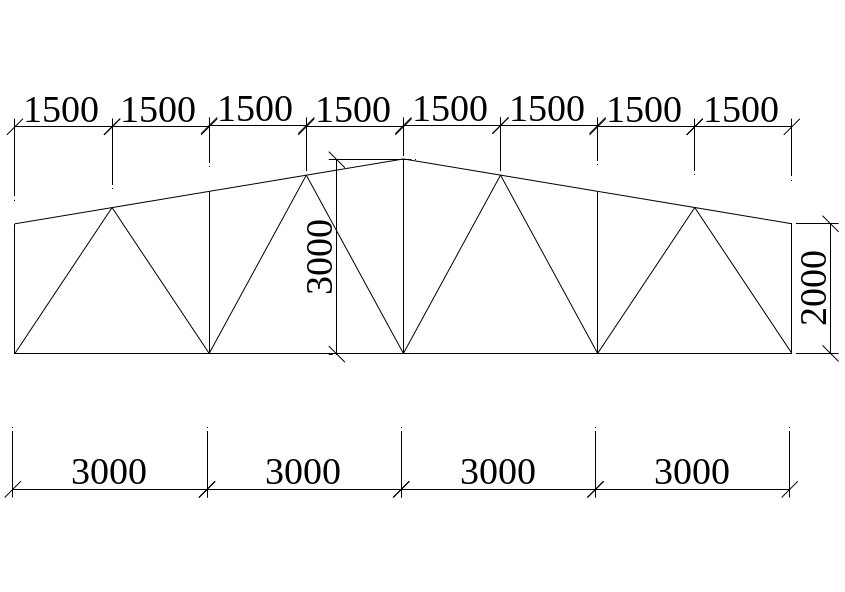Рис.34 Исходная ферма

При построении диаграммы следует придерживаться следующего алгоритма:

1. Необходимо изобразить в масштабе схему фермы с приложенными в узлах внешними силами и опорными реакциями (определяются заранее) так, чтобы их векторы расположились вне контура фермы (рис.35)

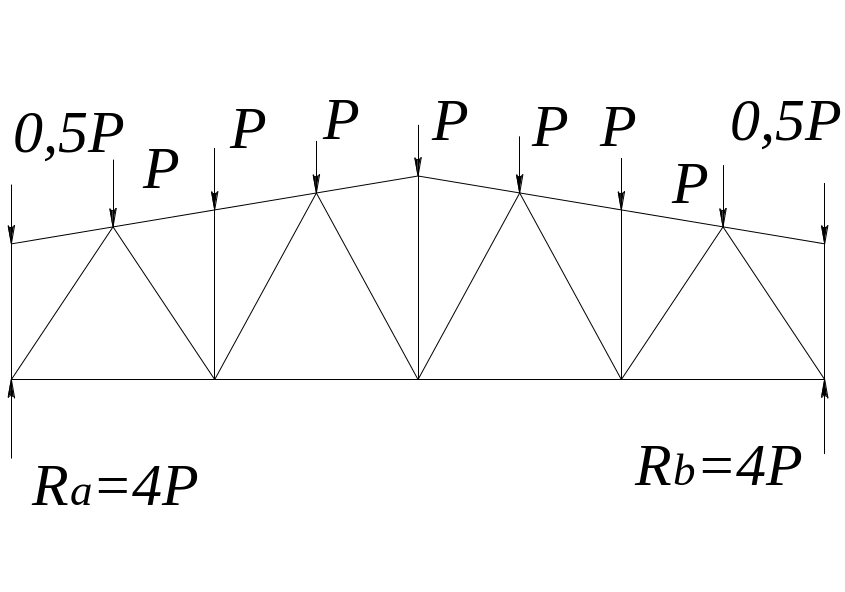
Рис.35 Ферма, загруженная вертикальными усилиями

2. Следует присвоить имя пространству (полю) между силами и стержнями фермы. Участки фермы между соседними внешними силами, а также части плоскости внутри решетки образуют, соответственно, так называемые, наружные и внутренние поля (районы) фермы (рис.36).

Рис.36 Ферма с обозначенными полями

Наружные поля следует обозначить буквами (а, б, в…) в обход контура фермы по часовой стрелке, а внутренние - цифрами (1, 2, 3, ...). Обозначение полей необходимо начинать с верхней части фермы слева.

3. Принять масштаб единицы силы.

4. Построить векторный многоугольник внешних сил. Для этого рассматривают ферму слева по часовой, последовательно обходя от одного поля (буквенного) к другому. Откладывают величины сил в соответствующем направлении и масштабе. Многоугольник должен быть замкнутым (система находится в равновесии), в противном случае опорные реакции определены неверно (рис.37).

5. Последовательно построить замкнутые силовые многоугольники для каждого узла фермы с использованием полученных имен полей:

• построение начинается с узла фермы, в котором сходятся два неизвестных стержня, с левой части фермы;

• стержни в узле начинают рассматривать по часовой стрелке, сверху;

• усилия на диаграмме должны быть параллельны соответствующим стержням на ферме;

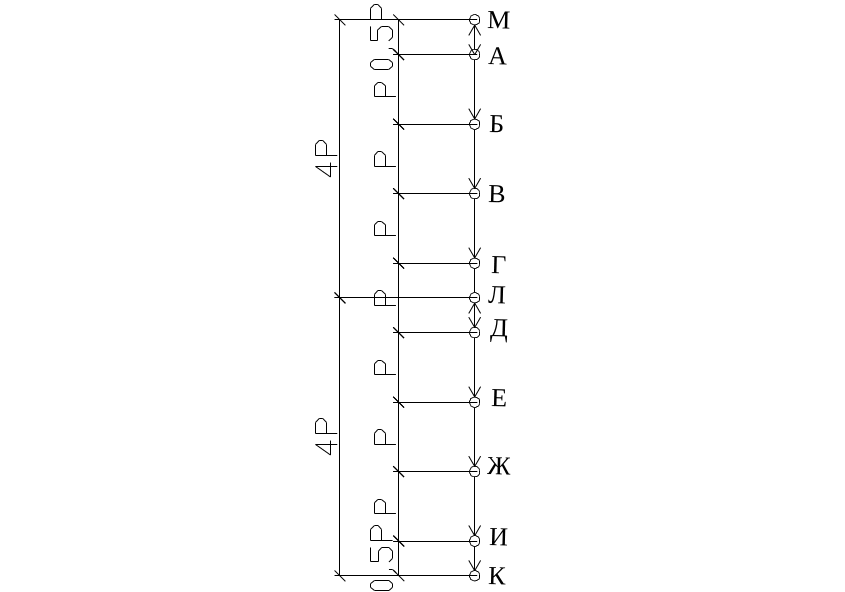Рис.37 Диаграмма внешних сил

• на диаграмме определяется известная точка (А) первого стержня фермы (А-1), через нее проводится первая линия (А-1) параллельная соответствующему стержню (А-1) (при этом считается, что стержень уже рассмотрен);

• на диаграмме определяется известная точка (М) второго стержня фермы (М-1), через нее проводится вторая линия (М-1) параллельная соответствующему стержню (М-1) (при этом считается, что стержень уже рассмотрен) при пересечении первой (А-1) и второй (М-1) линий получается точка (1), которая является общей (это поле внутри фермы смежное с наружными полями);

• усилие на диаграмме начинается и заканчивается именем поля, граничащего с соответствующим стержнем на ферме. Диаграмма должна иметь замкнутый вид, в противном случае она построена неверно.

Пример пошагового построения диаграммы усилий

(рис.38-53).

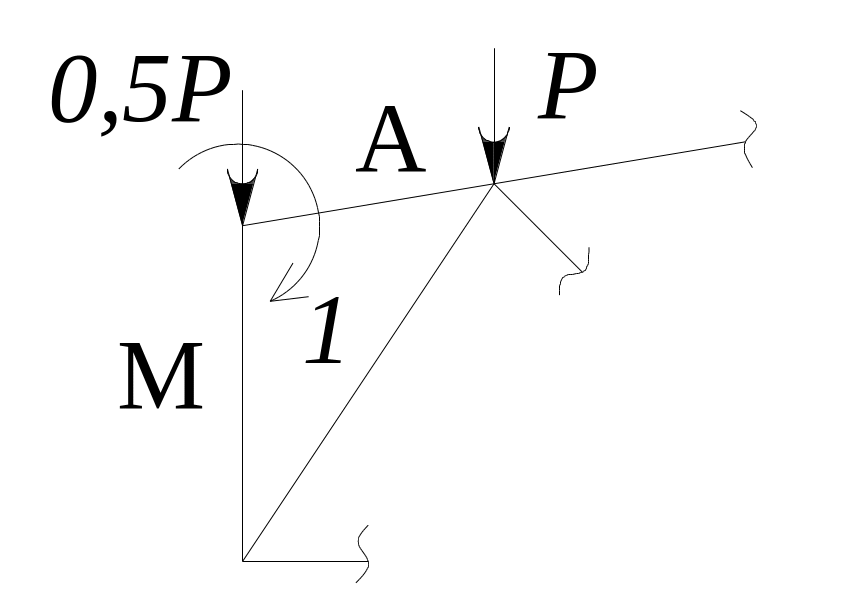
Рис.38. Определяем узел с двумя неизвестными стержнями. Рассматриваем первый стержень сверху по часовой – (А-1). На диаграмме усилий находим точку либо (А), либо (1).

Рис. 39. На диаграмме усилий проводим линию (А-1) параллельно стержню (А-1) через известную точку (А); Проводим линию (М-1) параллельно стержню (М-1) через известную точку (М). На пересечении линий (М-1) и (А-1) получаем точку (1). Считаем, что стержни (А-1) и (М-1) известны после проведения линий на диаграмме.

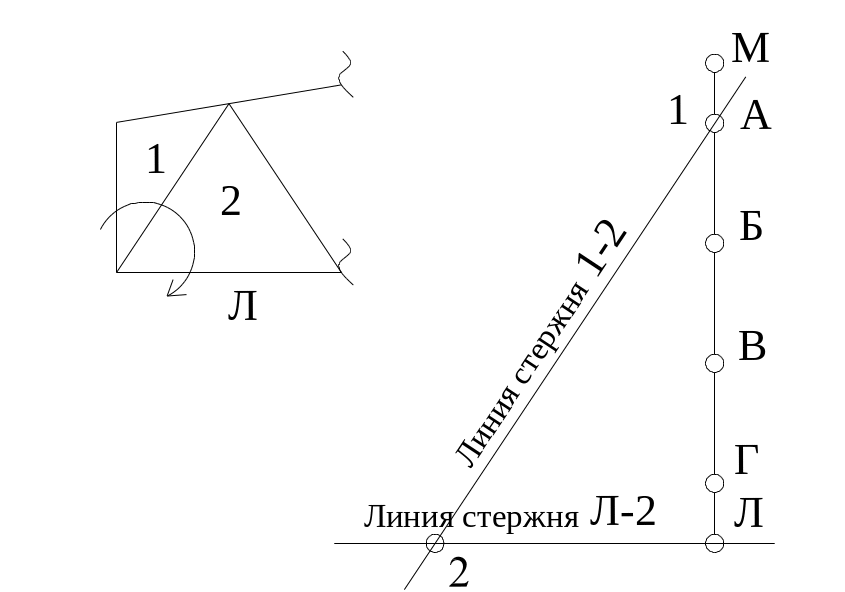
Рис. 40. Рассматривается следующий узел с двумя неизвестными стержнями. Первый стержень (1-2). Проводим на диаграмме линию (1-2) параллельную стержню (1-2) через точку (1). Проводим линию (Л-2) параллельно стержню (Л-2) через точку (Л). На пресечении получаем точку 2.

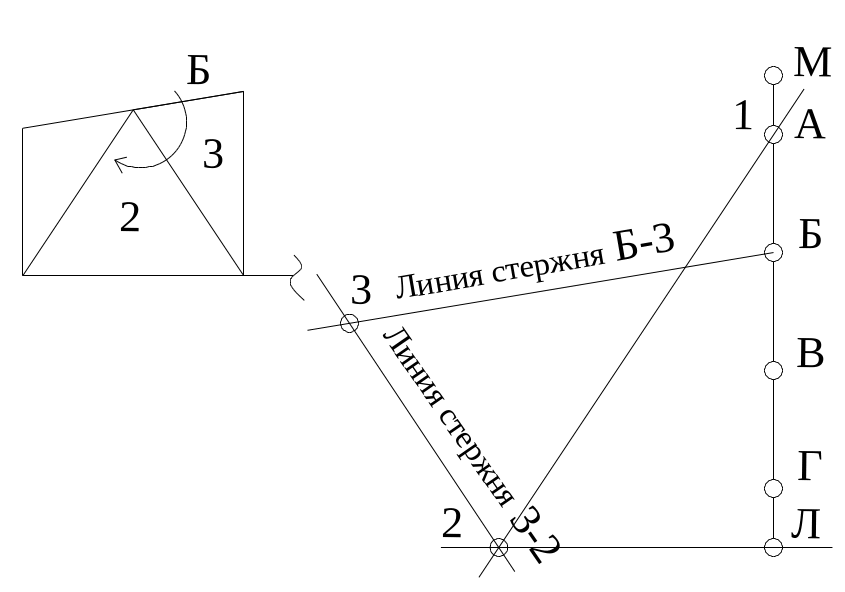
Рис. 41. Рассматривается следующий узел с двумя неизвестными стержнями. Первый стержень (Б-3). Проводим на диаграмме линию (Б-3) параллельную стержню (Б-3) через точку (Б). Проводим линию (2-3) параллельно стержню (2-3) через точку (2). На пресечении получаем точку 3.

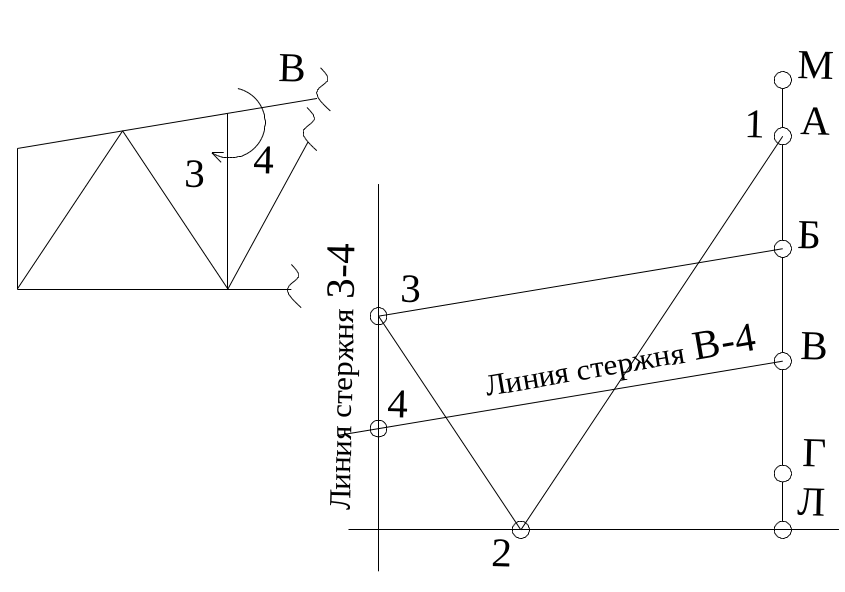
Рис. 42. Рассматривается следующий узел с двумя неизвестными стержнями. Первый стержень (В-4). Проводим на диаграмме линию (В-4) параллельную стержню (В-4) через точку (В). Проводим линию (3-4) параллельно стержню (3-4) через точку (3). На пресечении получаем точку 4.

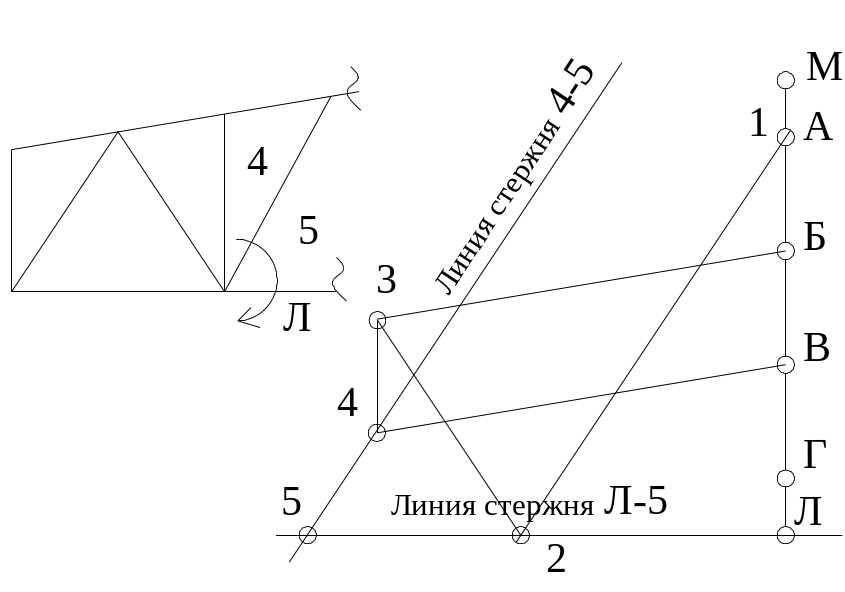
Рис. 43. Рассматривается следующий узел с двумя неизвестными стержнями. Первый стержень (4-5). Проводим на диаграмме линию (4-5) параллельную стержню (4-5) через точку (4). Проводим линию (Л-5) параллельно стержню (Л-5) через точку (Л). На пресечении получаем точку 5.

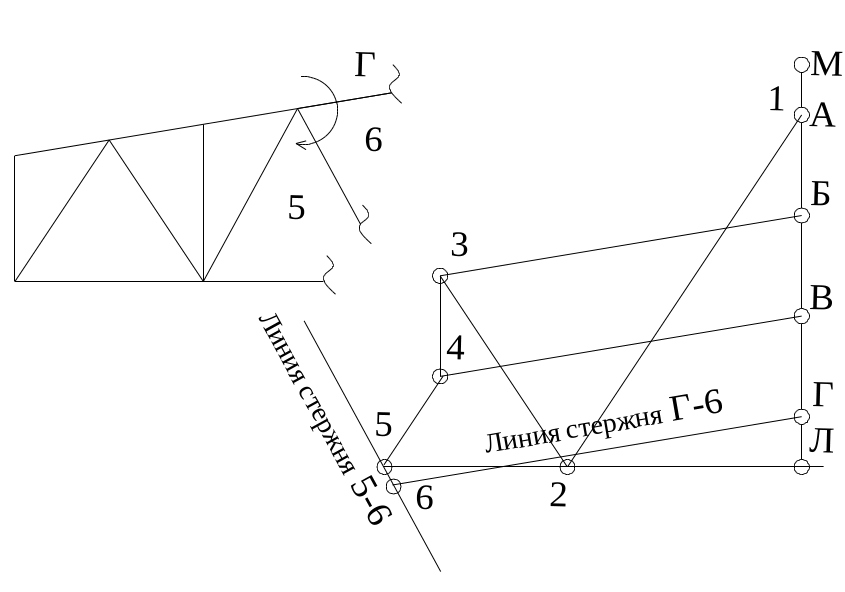
Рис. 44. Рассматривается следующий узел с двумя неизвестными стержнями. Первый стержень (Г-6). Проводим на диаграмме линию (Г-6) параллельную стержню (Г-6) через точку (Г). Проводим линию (5-6) параллельно стержню (5-6) через точку (5). На пресечении получаем точку 6.

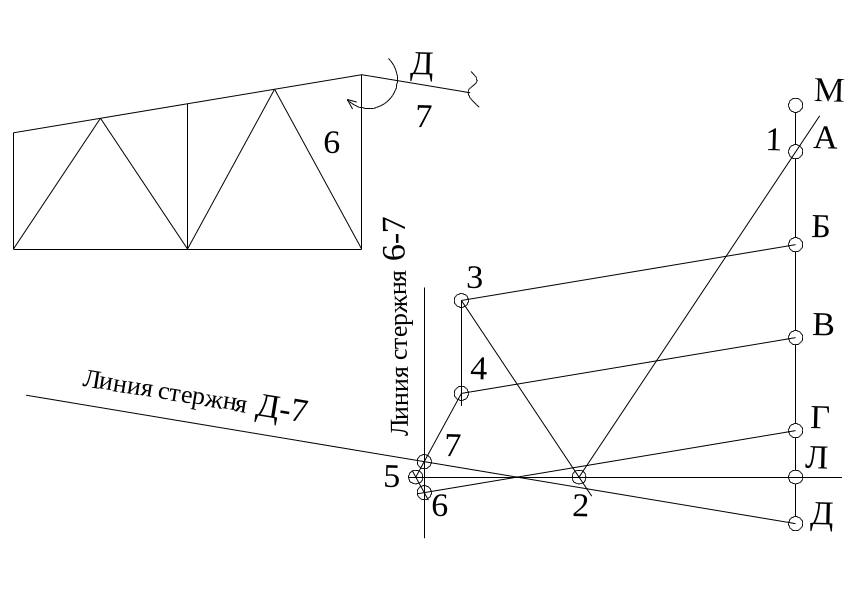
Рис. 45. Рассматривается следующий узел с двумя неизвестными стержнями. Первый стержень (Д-7). Проводим на диаграмме линию (Д-7) параллельную стержню (Д-7) через точку (Д). Проводим линию (7-6) параллельно стержню (7-6) через точку (6). На пресечении получаем точку 7;

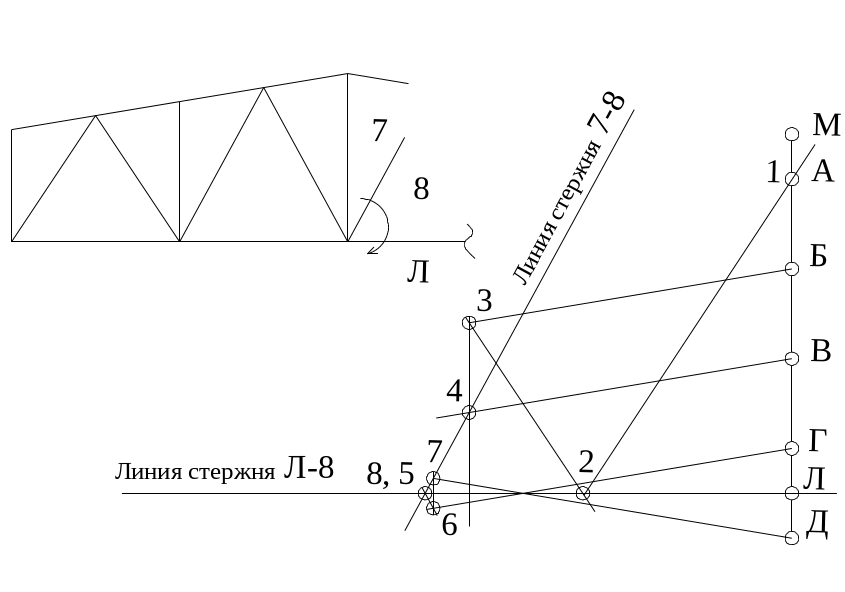
Рис. 46. Рассматривается следующий узел с двумя неизвестными стержнями. Первый стержень (7-8). Проводим на диаграмме линию (7-8) параллельную стержню (7-8) через точку (7). Проводим линию (Л-8) параллельно стержню (Л-8) через точку (Л). На пресечении получаем точку 8.

Рис. 47. Рассматривается следующий узел с двумя неизвестными стержнями. Первый стержень (Е-9). Проводим на диаграмме линию (Е-9) параллельную стержню (Е-9) через точку (Е). Проводим линию (8-9) параллельно стержню (8-9) через точку (8). На пресечении получаем точку 9.

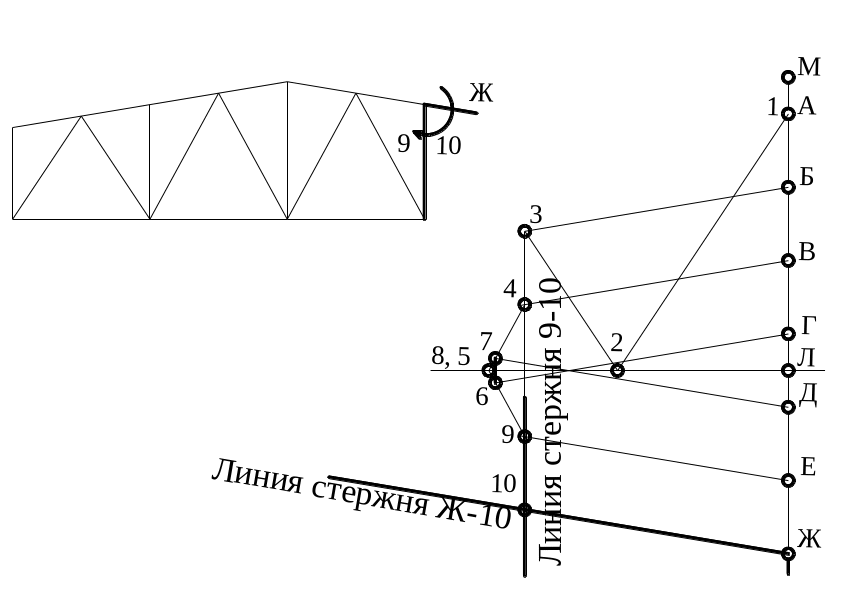
Рис. 48. Рассматривается следующий узел с двумя неизвестными стержнями. Первый стержень (Ж-10). Проводим на диаграмме линию (Ж-10) параллельную стержню (Ж-10) через точку (Ж). Проводим линию (9-10) параллельно стержню (9-10) через точку (9). На пресечении получаем точку 10.

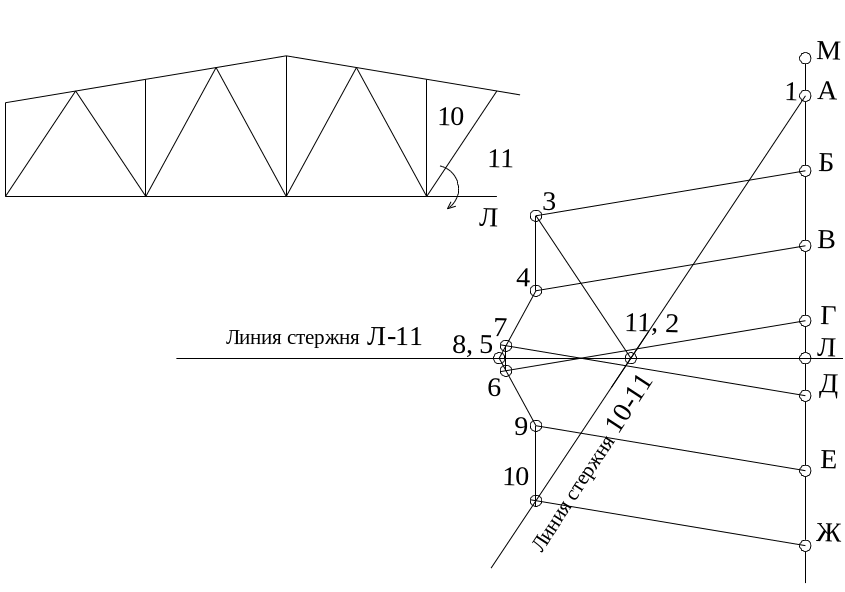
Рис.49. Рассматривается следующий узел с двумя неизвестными стержнями. Первый стержень (10-11). Проводим на диаграмме линию (10-11) параллельную стержню (10-11) через точку (10). Проводим линию (Л-11) параллельно стержню (Л-11) через точку (Л). На пресечении получаем точку 11.

Рис. 50. Рассматривается следующий узел с двумя неизвестными стержнями. Первый стержень (И-12). Проводим на диаграмме линию (И-12) параллельную стержню (И-12) через точку (И). Проводим линию (11-12) параллельно стержню (11-12) через точку (11). На пресечении получаем точку 12.

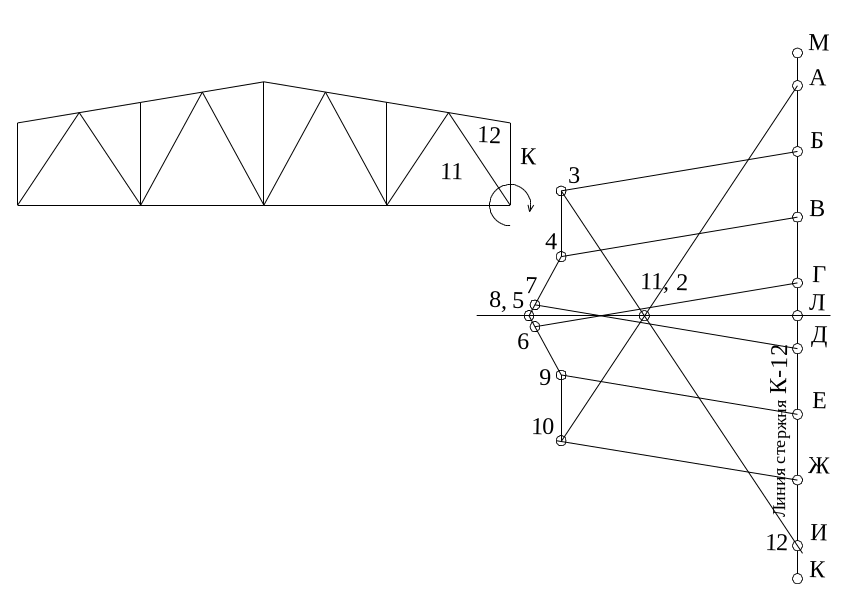
Рис. 51. Рассматривается следующий узел с двумя неизвестными стержнями. Первый стержень (К-12). Проводим на диаграмме линию (К-12) параллельную стержню (К-12) через точку (К). Проводим линию (11-12) параллельно стержню (11-12) через точку (11). На пресечении получаем точку 12. Точка должна совместиться с точкой полученной на предыдущем этапе. Диаграмма должна иметь замкнутый вид. В противном случае она построена неверно.

6. Определить величины усилий в стержнях фермы. Используя принятый масштаб, измерить на диаграмме длины линий соответствующих стержней. Результаты заносятся в таблицу усилий (табл.4).

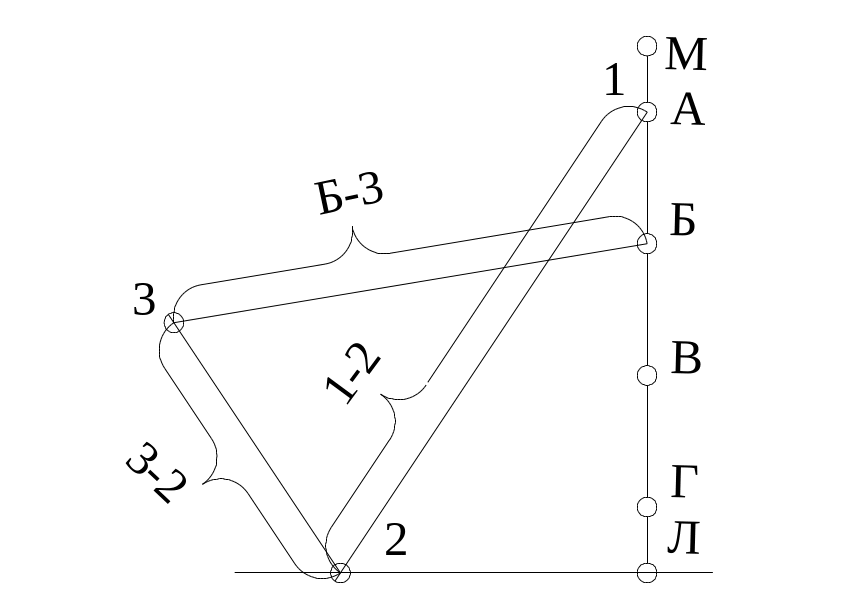
Рис. 52. Расстояния между точками на диаграмме соответствуют усилиям в стержнях. Например, усилие в стержне Б-3 - расстояние между точками Б и 3.

6. Определить знак усилия в стержне (сжатие - растяжение). Знак усилия определяем в следующей последовательности:

• выбираем узел, где примыкает стержень в котором необходимо определить знак усилия;

• стержень в узле рассматривается по часовой стрелке;

• определяется последовательность имени стержня (направление стрелки усилия): читается имя поля до стержня, имя поля после стерня;

• на диаграмме эта последовательность показывает направление действия силы (направление стрелки усилия). Имя поля до стержня, что соответствует началу направления усилия (начало стрелки), затем по линии усилия находится имя поля после стержня (конец стрелки), что соответствует концу направления усилия. При параллельном переносе в узел стрелка показывает направление усилия - от узла стержень растянут, к узлу - сжат.

Пример пошагового определения знака усилия приведен на рис.53.

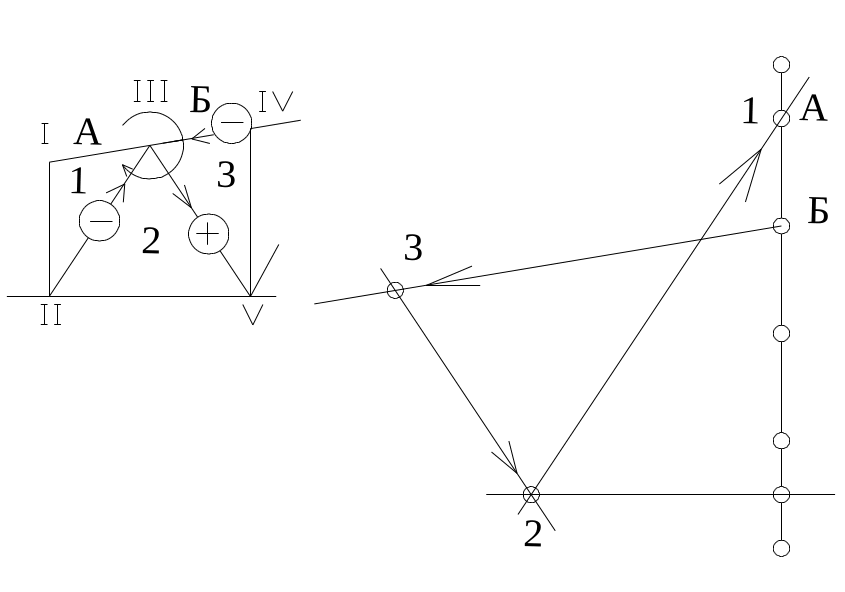
Рис. 53. Определение знака усилий. Рассмотрим узел, обозначенный цифрой (III). По часовой стрелке читаем названия стержней (3-2;). На диаграмме начало стрелки (3), конец стрелки (2). Переносим направление стрелки с диаграммы на узел (III). Стрелка показывает направление усилия от узла (III), стержень (3-2) растянут (знак +).

Для определения расчетных усилий в стержнях фермы составляется таблица усилий (табл.4), включающая усилия от постоянных и временных нагрузок. Расчетные усилия получают суммированием отдельных составляющих в их сочетании.

При расчете фермы можно пользоваться загружением единичной нагрузкой.

В таблице 4 обозначения колонок:

1 – наименование стержней, например, верхний пояс А-1, Б-3.

2 – усилия в стержнях от единичной вертикальной узловой силы (с учетом знака, «+»- растяжение, «-» - сжатие).

3 – усилия в стержнях от постоянной нагрузки (перемножение 2 столбца на значение постоянной нагрузки Р_П (ур.18)).

4 и 5 – усилия в стержнях от снеговой нагрузки с коэффициентом сочетания ψ=1 и 0,9 (перемножение 2 столбца на значение снеговой нагрузки Р_с (ур.19)).

6 и 7 – усилия в стержнях от единичного опорного момента слева (справа).

8 и 9 – усилия в стержнях от опорного момента слева (справа) (перемножением 6 столбца на величину момента слева (справа)),

10 и 11 (12,13) – усилия в стержнях от ветровой нагрузки ветер справа (слева) с коэффициентом ψ=1 и 0,9.

14 – номера усилий (см.примечание табл.4)

15 и 16 – максимальные усилия в стержнях фермы, полученные сложением усилий от постоянных и временных нагрузок с учетом возможных их сочетаний.

Расчет усилий в стержнях фермы

Таблица 4

№ стержня	Усилия от единичной нагрузки, Р=1	Усилия от постоянной нагрузки, Р=Рп, кН	Усилия от снеговой нагрузки, Р=Рс, кН		Усилия от опорных моментов, кН				Усилия от ветровой нагрузки				Расчетные усилия, максимальные, кН
									слева		справа
			ψ=1	ψ=0,9	Мл=1	Мпр=1	Мл= Мл	Мпр= Мпр	ψ=1	ψ=0,9	ψ=1	ψ=0,9	Сочетание усилий	Сжатие: (-)	Растяжение: (+)
№ усилий		1	2а	2б			3	4	5а	5б	6а	6б
1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
														-	+

Примечание: При сочетании усилий рекомендуется получить максимальные усилия сжатия и растяжения.

Возможные варианты сочетаний: при ψ=1 – 1+2; 1+3; 1+4; 1+5; 1+6;

при ψ=0,9 – 1+2б+3б+4б+5б; 1+2б+3б+4б+6б; 1+3б+4б+5б; 1+3б+4б+6б;

1+2б+5б; 1+2б+6б;

- усилие суммируется при совпадении их знаков (–,+), в случае не совпадения знаков усилие не учитывается.

Проверки прочности сечений стержней фермы

Таблица 5

№ стержня	Расчетные усилия, максимальные, кН		Сечение, мм	Площадь, А, см2	lx/ly, см	ix/iy, см	λx/λy	[λ]	φmin	Проверка сечений, σ≤Ryγc, кПа
	Сжатие (-)	Растяжение, (+)								σ=N/Aнт	σ=N/φA
1	2	3	4	5	6	7	8	9	10	11	12