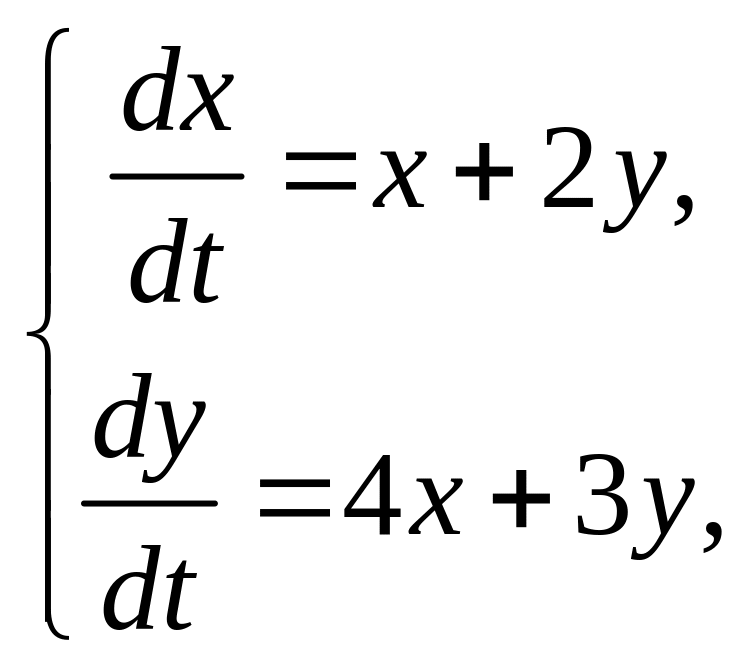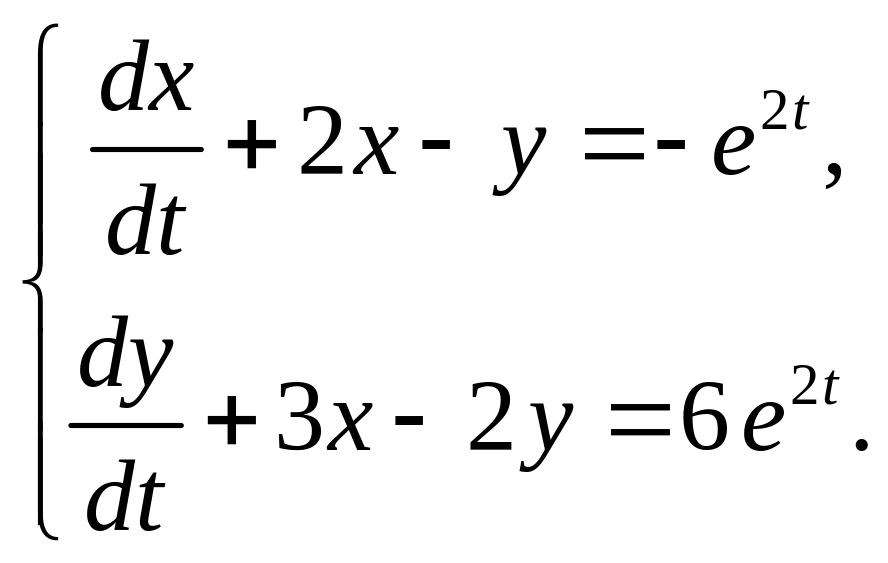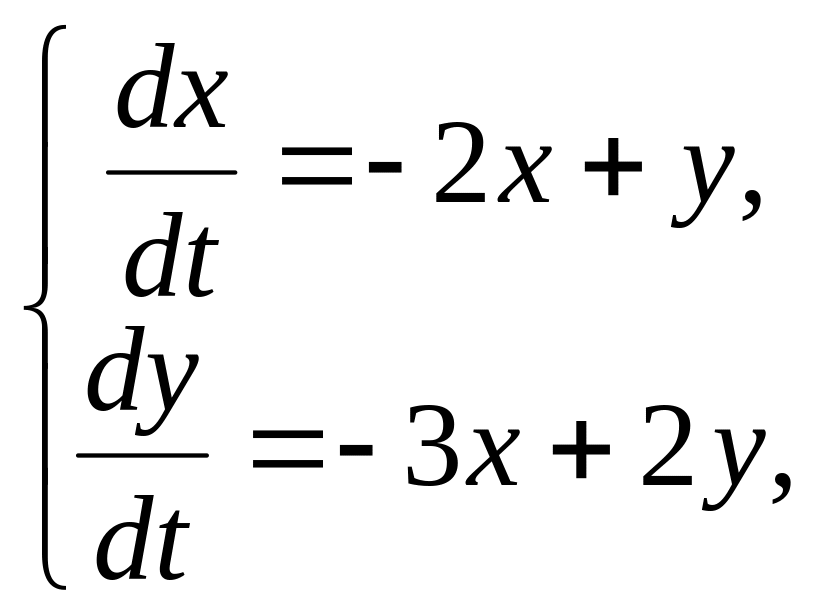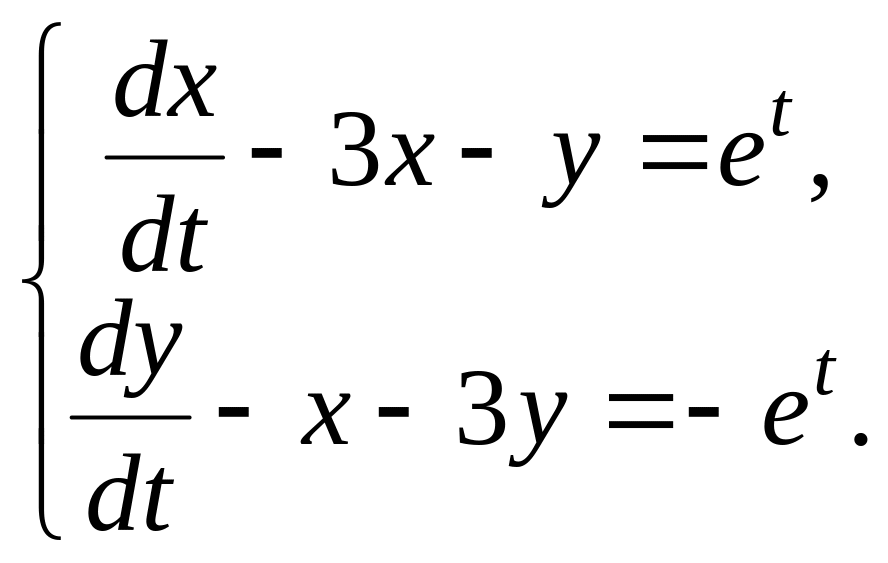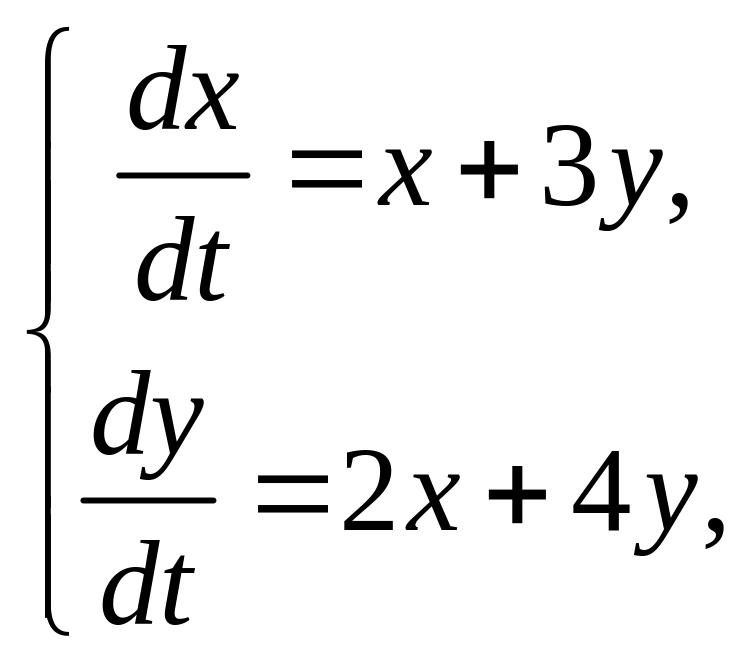Контрольная работа №4 (дифференциальные уравнения)
СЕМЕСТР 2
Вариант 1
1. Найти общий или частный интеграл (решение) дифференциального уравнения первого порядка:
а)
|
б)
|
в)
|
г)
|
д)
|
е)
|
,
,
,
2. Найти общий или частный интеграл (решение) дифференциального уравнения, допускающего понижения порядка:
а)
|
б)
|
3. Найти частное решение однородного линейного дифференциального уравнения второго порядка:
а)
|
б)
|
в)
|
|
4. Найти общее решение неоднородного линейного дифференциального уравнения второго порядка:
а)
|
б)
|
в)
|
г)
|
5. Найти общее решение линейного дифференциального уравнения методом вариации постоянных (методом Лагранжа):
.
6. Найти решение системы дифференциальных уравнений:
а)
|
б)
|
Вариант 2
1. Найти общий или частный интеграл (решение) дифференциального уравнения первого порядка:
а)
|
б)
|
в)
|
г)
|
д)
|
е)
|
,
,
,
.2. Найти общий или частный интеграл (решение) дифференциального уравнения, допускающего понижения порядка:
а)
|
б)
|
.3. Найти частное решение однородного линейного дифференциального уравнения второго порядка:
а)
|
б)
|
в)
|
|
4. Найти общее решение неоднородного линейного дифференциального уравнения второго порядка:
а)
|
в)
|
б)
|
г)
|
5. Найти общее решение линейного дифференциального уравнения методом вариации постоянных (методом Лагранжа):
.
6. Найти решение системы дифференциальных уравнений:
а)
|
б)
|
Вариант 3
1. Найти общий или частный интеграл (решение) дифференциального уравнения первого порядка:
а)
|
б)
|
в)
|
г)
|
д)
|
е)
|
,
,
,
.2. Найти общий или частный интеграл (решение) дифференциального уравнения, допускающего понижения порядка:
а)
|
б)
|
3. Найти частное решение однородного линейного дифференциального уравнения второго порядка:
а)
|
б)
|
в)
|
|
4. Найти общее решение неоднородного линейного дифференциального уравнения второго порядка:
а)
|
в)
|
б)
|
г)
|
5. Найти общее решение линейного дифференциального уравнения методом вариации постоянных (методом Лагранжа):
.
6. Найти решение системы дифференциальных уравнений:
а)
|
б)
|
