40. Электр өрісінің кернеулік векторының ағыны. Гаусс теоремасы.
векторының
ағыны өтетін өте кіші
элементар ауданды алайық. Оған түсірілген
нормаль
электр өрісінің векторы
-мен
бұрышын жасайды делік. Бұл ауданды қиып
өтетін элементар ағын
:
·
,
мұндағы
кернеулік
векторының ауданға түсірілген
нормаль бағытына проекциясы;
-вектор,
ол модулі
-ке
тең де, бағыты
-нің
бағытымен бағыттас.
6
дәріс
Кез
келген
ауданнан өтетін
векторының ағыны
:
болады.
Осыған байланысты атап өтетін бір жай:
аудан тұйық болған кезде, оған түсірілген
нормальдың оң бағыты ретінде сыртқы
нормаль алынады: яғни нормальдың бәрі
ауданнан сыртқа қарай бағытталады.
Нүктелік заряд өрісін қарастырайық.
Заряд
кез келген пішіндегі тұйықталған беттің
ішіне орналасқан делік. Кіші
ауданынан
өтетін элементар ағын
:
.
Бұған
нүктелік зарядтың электр өрісінің
мәнін қойғанда:
бұл
жердегі
- элементар ауданға тірелуші, төбесі
нүктелік зарядта орналасқан денелік
бұрыш.
теңдігін
интегралдасақ, толық ағын
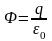-ге
тең болады.
-тың
бұл мәнін
формуласының сол жағына апарып қойғанда:
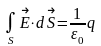болады.
Заряд кез келген пішіндегі беттің тұйық
ішінде жатқандықтан
бұрышы
-ден
аз да, көп те болуы мүмкін. Сондықтан
мен
нөлден көп те, нөлден аз да болар еді,
яғни заряд тұйық беттің сыртында
орналасқан жағдайда, ондай ауданнан
-векторының
ағыны нөлге тең болады. Электр өрісін
…,
нүктелік заряд тудыратын болса, онда
суперпозиция принципі бойынша қорытқы
ағын:
Егер
зарядтар тұйық беттің ішіне орналасқан
болса, онда теңдіктің оң жағындағы әр
интеграл
-ге
тең болар еді. Сондықтан:
деп
жазуға болады. Бұл
теңдеу Гаусс теоремасының математикалық
өрнегі болып табылады. Оның анықтамасы:
вакуумдегі электр өрісі векторының
кез келген пішіндегі тұйық бет бойынша
ағыны, оның ішінде жатқан зарядтардың
алгебралық қосындысын электр тұрақтысына
-ге
бөлгенге тең. Егер зарядтар берілген
көлемде
тығыздықпен үздіксіз таралып орналасқан
болса, осы
көлемінің ішіндегі жиынтық заряд:
Осы
теңдікті
ескере отырып, Гаусс теоремасын электр
өрісі үшін төмендегідей түрде жазуға
болады:
.
41. Электростатикалық өрісте заряд орын ауыстырғанда істелінетін жұмыс.
Нүктелік зарядының өрісінде екінші нүктелік заряд 1-ші нүктеден 2-ші нүктеге қайсыбір траекториямен қозғалсын.
Орындалатын
элементар жұмыс
,
болғандықтан,
болады.
зарядын 1-ші нүктеден 2-ші нүктеге дейін
орын ауыстырғанда орындалатын жұмыс:
мұндағы
мен
-
зарядынан қозғалушы
орналасқан бастапқы және соңғы нүктелерге
дейінгі қашықтықтар. Осыған сәйкес
теңдігінен электростатикалық өрісте
жұмыс зарядтың жүріп өткен жолының
траекториясына байланысты емес екендігін
және тек қана 1-ші мен 2-ші нүктелердің
орнымен анықталатынын көруге болады.
Олай болса, бұл электрстатикалық өріс
потенциалды,
электрлік күштер консервативті
болады деген сөз. Егер
бірнеше нүктелік зарядтардың өрісінде
қозғалатын болса, оған суперпозиция
принципі бойынша,
күші әсер еткендіктен, атқарылатын
жұмыс әр күш жұмыстарының алгебралық
қосындысына тең, яғни
бұл
жердегі
мен
мөлшері
зарядтан
орналасқан бастапқы және соңғы нүктелерге
дейінгі қашықтық. Жоғарыдағы
формуладан
туындайтын тағы бір қорытынды
–электрстатикалық өрісте зарядтың
тұйық контурдың бойымен орын ауыстыру
жұмысының нөлге теңдігі, яғни
болуы. Егер қозғалушы зарядты бірлік
өлшемді зарядқа тең деп алсақ, онда
теңдіктен:
,
н/е
.
Бұл интеграл электрстатикалық өрістің
кернеулік векторының тұйық контур
бойымен циркуляциясы
деп аталады.
векторының циркуляциясы теоремасынан бірнеше маңызды қорытындылар шығаруға болады:
1) электрстатикалық өріс кернеулігінің күш сызықтары тұйық болуы мүмкін емес.
Шындығында да, егер векторының қандай да бір сызығы тұйық болса, онда осы сызық бойымен векторының циркуляциясын алсақ теориямен қарама-қайшылыққа келуші едік.
2) Суретте көрсетілген түрдегі электрстатикалық өрістің болуы мүмкін емес.
Егерде суретте көрсетілген үзік-үзік сызықтарға векторының циркуляциясы теоремасын қолданса, онда ол нөлден ерекше болады, ал ол теоремаға қарама-қайшы келеді.