2-й семестр / Электричество и магнетизм. Пособие по решению задач

УДК 537 (076) ББК 22.23

Э 45

Анищенко И.А.,Задерновский А.А., Пыркин А.Ю., Росляков В.А. Электричество и магнетизм: Учебное пособие по решению задач по физике. /МИРЭА - Российский технологический университет (РТУ МИРЭА). – М., 2018. – 68 с./

Учебное пособие по решению задач предназначено для бакалавров всех направлений подготовки и специалистов всех специальностей, изучающих вторую часть курса физики «Электричество и магнетизм». Пособие содержит основные формулы, используемые при решении задач, 50 задач с решениями, 100 задач для самостоятельного решения, таблицу основных физических постоянных, вопросы для подготовки к экзамену и список рекомендуемой литературы. Учебный материал соответствует программе курса физики, изучаемого в РТУ МИРЭА.

Учебное пособие издается в авторской редакции.

Авторский коллектив: Анищенко Инна Альбертовна, Задерновский Анатолий Андреевич, Пыркин Андрей Юрьевич, Росляков Владимир Александрович

Рецензенты:

Астапенко Валерий Александрович, профессор, д.ф.-м.н, профессор, Московский фи- зико-технический институт (государственный университет).

Кротов Юрий Александрович, к.ф.-м.н, доцент, ученый секретарь, Акционерное общество «Научно-исследовательский институт «Полюс» имени М.Ф. Стельмаха»

Издается в электронном виде по решению редакционно-издательского совета РТУ МИРЭА.

Минимальные системные требования:

Наличие операционной системы Windows, поддерживаемой производителем. Наличие свободного места в оперативной памяти не менее 128 Мб.

Наличие свободного места в памяти хранения (на жестком диске) не менее 30 Мб. Наличие интерфейса ввода информации.

Дополнительные программные средства: программа для чтения pdf-файлов (Adobe Reader). Подписано к использованию по решению Редакционно-издательского совета МИРЭА - Российского технологического университета от ___ __________ 2018 г.

Тираж 10

©Анищенко И.А.,Задерновский А.А., Пыркин А.Ю., Росляков В.А. 2018

©МИРЭА - Российский технологический университет (РТУ МИРЭА), 2018

РАЗДЕЛ 1. ЭЛЕКТРОСТАТИКА. ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК. 12

ПРЕДИСЛОВИЕ

В основу принятой в федеральном государственном бюджетном образовательном учреждении высшего образования «МИРЭА - Российский технологический университет» (РТУ МИРЭА) системы обучения положена фундаментальная подготовка студентов на младших курсах в сочетании с производственным обучением на старших курсах. При этом, одной из важнейших дисциплин в теоретической и практической подготовке современного инженера является курс физики. В соответствии с учебными планами курс физики в РТУ

4

МИРЭА разбит на три части: (1) механика и молекулярная физика, (2) электричество и магнетизм, (3) оптика и атомная физика.

Предлагаемое учебное пособие по решению задач по второй части курса физики предназначено для бакалавров всех направлений подготовки и специалистов всех специальностей. Материал учебного пособия содержит: основные формулы, используемые при решении задач, подробное решение 50 типовых задач, 100 задач с ответами для практических занятий, таблицу основных физических постоянных, вопросы для подготовки к экзамену и список рекомендуемой учебной литературы.

При составлении и подборе задач для учебного пособия учтена специфика направлений подготовки бакалавров и специальностей, по которым ведется подготовка инженеров в РТУ МИРЭА. При этом авторы использовали как свои, оригинальные задачи, так и наиболее удачные задачи из ряда учебнометодических пособий и сборников задач, перечисленных в списке рекомендованной литературы.

Авторы выражают глубокую благодарность преподавателям кафедры физики РТУ МИРЭА, принявшим участие в анализе задач и сделавшим ценные замечания при прочтении рукописи.

ОСНОВНЫЕ ФОРМУЛЫ

Электричество

Закон Кулона:

F 1 Q1Q2 , 4 0 r2

где F - сила взаимодействия точечных зарядов Q1 и Q2 , r - расстояние между зарядами, - диэлектрическая проницаемость, 0 - электрическая постоянная.Напряженность электрического поля и потенциал:

Е = F/Q, П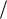Q ,

где П - потенциальная энергия точечного положительного заряда Q, находящегося в данной точке поля (при условии, что потенциальная энергия заряда, удаленного в бесконечность, равна нулю).

Сила, действующая на точечный заряд, находящийся в электрическом поле, и потенциальная энергия этого заряда:

F = QE, П Q .

Напряженность и потенциал поля, создаваемого системой точечных зарядов

5

(принцип суперпозиции электрических полей):

где Ei , i - напряженность и потенциал в данной точке поля, создаваемые i - м зарядом.

Напряженность и потенциал поля, создаваемого точечным зарядом:

где r - расстояние от заряда Q до точки, в которой определяются напряженность и потенциал.

Напряженность и потенциал поля, создаваемого проводящей сферой радиусом R с зарядом Q на расстоянии r от центра сферы:

Линейная плотность заряда:

dQdl

Поверхностная плотность заряда:

dQdS

Поток вектора напряженности E электрического поля через замкнутую поверхность площади S, помещенную в неоднородное электрическое поле:

E Ends

S

где En - проекция вектора напряженности электрического поля на нормаль к поверхности.

Теорема Остроградского - Гаусса. Поток вектора напряженности электрического поля через любую замкнутую поверхность, охватывающую заряды Q1, Q2,

Q3,…, Qn:

6

Напряженность поля, создаваемого бесконечной равномерно заряженной прямой линией (нитью) или бесконечно длинным цилиндром:

где - линейная плотность заряда, r - расстояние от нити или оси цилиндра до точки, в которой вычисляется напряженность поля.

Напряженность поля, создаваемого бесконечной равномерно заряженной плоскостью:

E , 2 0

где - поверхностная плотность заряда.

Связь потенциала поля с напряженностью поля:

E grad

Электрический момент диполя:

p Q l ,

где Q - заряд; l - плечо диполя (векторная величина, направленная от отрицательного заряда к положительному и численно равная расстоянию между зарядами).

Механический (вращательный) момент сил, действующий на диполь с электрическим моментом р, помещенный в однородное электрическое поле с напряженностью Е:

М = [p E] или М = рЕ sin ,

где - угол между направлениями векторов р и Е.

Работа сил поля по перемещению заряда Q из точки поля с потенциалом 1 в точку с потенциалом 2 :

A12 Q 1 2

Электроемкость проводника и конденсатора:

Спроводника = Q/ или Сконденсатора = Q/ U,

где - потенциал проводника (при условии, что в бесконечности потенциал проводника принимается равным нулю), U - разность потенциалов пластин конденсатора.

Электроемкость уединенной проводящей сферы радиусом R:

C 4 0 R ,

Электроемкость плоского конденсатора:

7

C 0S , d

где S - площадь пластины (одной) конденсатора, d - расстояние между пластинами.

Электроемкость батареи, состоящей из N конденсаторов:

i1

Энергия заряженного конденсатора:

W CU 2 QU Q2 . 2 2 2C

Связь вектора поляризации (поляризованности) P с напряженностью Е среднего макроскопического поля в диэлектрике:

P0E

- диэлектрическая восприимчивость.

Связь между вектором индукции D и вектором напряженности Е электриче-

ского поля в однородных диэлектриках:

D0E P

Связь диэлектрической проницаемости с диэлектрической восприимчиво-

стью :

1

Связь между поверхностной плотностью связанных зарядов и нормальной

составляющей вектора поляризации Pn:

Pn

Объемная плотность энергии электростатического поля:

Сила электрического тока:

I dQdt ,

где dQ - заряд, прошедший через поперечное сечение проводника, за время dt .Плотность электрического тока тока:

j dIds env ,

8

где S - площадь поперечного сечения проводника, е - заряд частицы, n - концентрация частиц, v - скорость направленного движения частиц.

гебраическая сумма падений напряжений (произведений сил токов на сопро-

m

тивления участков), E j - алгебраическая сумма э.д.с.

j1

Сопротивление R и проводимость G проводника:

R = l/S , G = S/l,

где - удельное сопротивление, - удельная проводимость, l - длина проводника, S - площадь поперечного сечения проводника.

A IUt I 2Rt U 2 t . R

Мощность тока:

P IU I 2R U 2 . R

9

Законы Ома и Джоуля-Ленца в дифференциальной форме: j = E, w= E 2,

где - удельная проводимость, Е – вектор напряженности электрического поля, j – вектор плотности тока, w - плотность мощности, выделяемой в проводнике.

Магнетизм

Связь вектора магнитной индукции В с напряженностью H магнитного поля:

B 0H

где - магнитная проницаемость изотропной среды, 0 - магнитная постоянная. В вакууме =1, в парамагнетике >1, в диамагнетике <1, в ферромагне-

тике (H ) 1.

Закон Био-Савара-Лапласа:

где dB - индукция магнитного поля, создаваемого элементом проводника длиной dl c током I, r - радиус-вектор, направленный от элемента проводника к точке, в которой определяется индукция, - угол между радиус-вектором и направлением тока в элементе проводника.

Магнитная индукция на оси кругового тока

где h - расстояние от центра витка до точки, в которой определяется магнитная индукция.

Магнитная индукция поля, создаваемого отрезком провода с током:

B 0 I (cos 1 cos 2 ) 4 r0

где r0 - расстояние от оси проводника до точки, в которой определяется магнитная индукция; 1 и 2 - углы между направлением тока и радиусами векторами, проведенными из концов проводника в точку наблюдения.

Магнитная индукция поля длинного соленоида:

B 0nI ,

где n – число витков, приходящихся на единицу длины соленоида.

Сила, действующая на проводник с током в магнитном поле (закон Ампера): dF I dl B или dF IdlBsin ,

где dl - длина элемента проводника, - угол между направлением тока в про-

10

воднике и вектором магнитной индукции В.

Магнитный дипольный момент плоского контура с током:

рm = nIS ,

где n - единичный вектор нормали к плоскости контура (направление вектора n связывается с направлением тока в контуре по правилу правого винта), I - сила тока, проходящего по контуру; S - площадь контура.

F = QE + Q[v×,B] ,

где Q - заряд частицы. v - скорость частицы, Е - вектор напряженности электрического поля, В - вектор магнитной индукции.

Магнитный поток:

Ф= Bn dS ( интегрирование ведется по всей поверхности).

S

В случае однородного поля и плоской поверхности:

Ф = ВS cos или Ф = Вn S,

где S - площадь контура, - угол между нормалью к плоскости контура и вектором магнитной индукции.

Работа по перемещению замкнутого контура в магнитном поле:

A I .

Э.д.с. индукции:

i ddt ,

где - потокосцепление (полный поток через N контуров).

Э.д.с. индукции, возникающая при движении проводника в магнитном поле: