Задача 3

Прямолинейный проводник с током силой I делает петлю в виде окружности радиуса R, касательную к проводнику. Прямолинейная часть проводника по обе стороны от точки касания окружности равна 2R. Найти магнитную индукцию в центре петли.

Решение:

I. Сделаем чертёж- рис.4.4.

Очевидно, что магнитное поле в центре петли (в точке 0) складывается из:

а) магнитного поля - в центре кругового тока и

б) поля 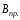- прямолинейного тока на расстоянии R от него,

То есть результирующее поле в центре петли по принципу суперпозиции равно векторной сумме:

а) Магнитная индукция в центре витка с током получена в конце примера 1, стр.80 (при z=0):

(4.13)

В соответствии с законом Био-Савара-Лапласа (4.1) этот вектор направлен перпендикулярно плоскости чертежа от наблюдателя.

б) Найдём магнитную индукцию - прямолинейного тока на расстоянии R от него, используя предложенную в начале этого семинара (стр.73-74) схему:

I. Сделаем чертёж – рис.4.5.

II. Выберем бесконечно малый элемент проводника dl. От этого элемента тока проведём вектор до заданной точки 0.

III. Запишем закон (4.1) для выбранного элемента тока:

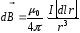
Этот вектор по правилу векторного произведения в точке 0 направлен перпендикулярно к плоскости чертежа от наблюдателя (правило правого винта – см. семинар №1, стр.7-8).

IV. Любой другой элемент тока этого проводника в заданной точке О создаёт магнитную индукцию такого же направления. Величина dВ:

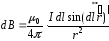(4.14)

угол между векторам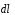и и 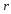на рис.4.4 обозначен через .

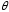V. Так как в данном случае реализуется ситуация, изложенная в схеме решения на стр.73 (п.V (а)) то, в соответствии с принципом суперпозиции результирующее поле прямолинейного тока найдём так:

(4.15)

Необходимо рассчитать интеграл, под знаком которого три переменные. Такой расчёт приведён в примере 1 семинара №2 на стр.30. Чтобы использовать для расчёта интеграла (4.15) равенства (2.17и 2.18), надо от 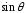перейти к 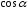- рис.4.5, при этом (см. условие задачи) пределы интегрирования по 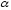будут (от 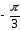до ):

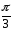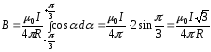(4.16)

Таким образом, магнитное поле прямолинейного тока:

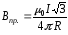(4.17)

VI. Результирующее магнитное поле кругового (4.13) и прямолинейного (4.17) токов с учётом их направлений в точке О равно:

Или (4.18)

Ответ:

Домашнее задание:

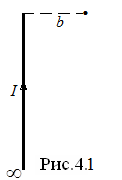
1. Определить с помощью принципа суперпозиции магнитную индукцию длинного проводника с током силой I=20 А, в точке, лежащей на перпендикуляре на расстоянии b=30 см от конца проводника – рис.4.1.

2. По проволочной рамке, имеющей форму правильного шестиугольника, идёт ток силой I=2 А. При этом в центре рамки образуется магнитное поле напряжённостью Н=33 А/м – рис.4.6. Найти длину проволоки, из которой сделана рамка.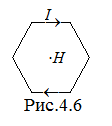

3. По прямолинейным длинным проводникам, находящимся на расстоянии а=10 см друг от друга, текут токи силой I₁=3 А и I₂=2 А. Определить, в каких точках магнитное поле отсутствует при одинаковом направлении токов. Предварительно с помощью принципа суперпозиции вывести расчётную формулу для магнитной индукции В, созданной прямолинейным бесконечно длинным током на произвольном расстоянии от него.

4. Два прямолинейных бесконечно длинных проводника с токами силой I₁=2 А и I₂=3 А расположены в одной плоскости перпендикулярно друг другу. Найти магнитную индукцию в точке А, которая отстоит от первого провода на расстояние а=10 см и от второго - на расстояние b=20 см. Предварительно с помощью принципа суперпозиции вывести расчётную формулу для магнитной индукции В, созданной прямолинейным длинным током.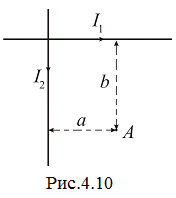

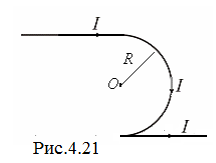
5. Найти магнитную индукцию поля в центре О полукольца радиуса R=0,5 м, соединенного с бесконечно длинными параллельными проводниками с расстоянием между ними а=2R – рис.4.21. В контуре течет ток силой I=1 А. Предварительно вывести расчётные формулы для магнитной индукции B в центре полукольца с током и для «полубесконечного» тока на перпендикуляре напротив его конца