
Семинар №9
Тема: Магнитостатика
.Закон
Био-Савара-Лапласа:
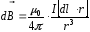 ,
где
,
где
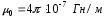 - магнитная
постоянная
- магнитная
постоянная
Закон
Ампера:

Принцип
суперпозиции:
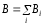
Схема решения задач магнитостатики с помощью закона Био-Савара-Лапласа и принципа суперпозиции.
I. Сделать чертёж в
соответствии с условием задачи –
рис.4.1.
II. Выбрать произвольный
бесконечно малый элемент длины проводника
 с
током силой I;
вектор
с
током силой I;
вектор
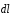 направлен по касательной к проводнику
вдоль направления тока в том месте, где
выбран
направлен по касательной к проводнику
вдоль направления тока в том месте, где
выбран
 (рис.4.1) – произведение (
(рис.4.1) – произведение (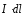 )
называют элементом тока.
)
называют элементом тока.
Провести
вектор
 от элемента тока до заданной точки А,
в которой надо определить величину и
направление напряжённости
от элемента тока до заданной точки А,
в которой надо определить величину и
направление напряжённости
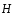 или магнитной индукции
или магнитной индукции
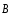 .
.
III. Записать в векторном
виде закон Био-Савара-Лапласа для
выбранного элемента тока (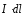 ):
):
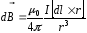 (4.1)
(4.1)
Используя правило векторного произведения
(см. семинар №1, стр.9-10), определить
направление вектора
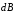 ,
созданного элементом тока в заданной
точке А.
,
созданного элементом тока в заданной
точке А.
IV. Определить в этой же
точке А
направления векторов
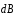 ,
созданных другими элементами тока
данного проводника.
,
созданных другими элементами тока
данного проводника.
По возможности определить направление
результирующего вектора
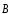 в данной точке, общую конфигурацию поля
в пространстве и записать модуль вектора
в данной точке, общую конфигурацию поля
в пространстве и записать модуль вектора
 :
:
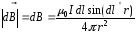 (4.2
(4.2
V. Далее учесть, что возможны 2 случая:
а) если в заданной
точке А
все векторы
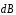 ,
созданные различными элементами тока,
направлены вдоль одной прямой, то,
применяя принцип суперпозиции (используя
для этого интегрирование выражения
(4.2)), найти величину результирующего
вектора
,
созданные различными элементами тока,
направлены вдоль одной прямой, то,
применяя принцип суперпозиции (используя
для этого интегрирование выражения
(4.2)), найти величину результирующего
вектора
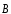 :
:
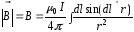 (4.3)
(4.3)
b) если в заданной
точке А
вектора
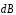 ,
созданные различными элементами тока,
направлены по-разному, то надо ввести
в этой точке систему координат ХY,
разложить вектор
,
созданные различными элементами тока,
направлены по-разному, то надо ввести
в этой точке систему координат ХY,
разложить вектор
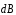 ,
созданный произвольным элементом тока,
на составляющие
,
созданный произвольным элементом тока,
на составляющие
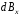 и
и
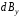 ,
введя угол
,
введя угол
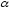 между вектором
между вектором
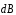 и осью Х:
и осью Х:
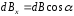
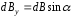
и,
используя принцип суперпозиции,
рассчитать составляющие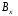 и
и
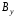 результирующего вектора
результирующего вектора
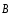 :
:
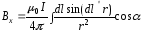 (4.4)
(4.4)
 (4.5)
(4.5)
Определить величину результирующего вектора магнитной индукции в заданной точке поля с помощью теоремы Пифагора:
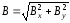 (4.6)
(4.6)
Найти
угол
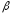 ,
задающий направление вектора
,
задающий направление вектора
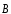 по отношению к оси Х:
по отношению к оси Х:
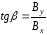 (4.7)
Зная
(4.7)
Зная
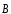 ,
можно определить напряжённость магнитного
поля
,
можно определить напряжённость магнитного
поля
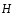 :
:
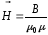 (4.8)
(4.8)
здесь
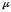 -
магнитная проницаемость среды. Для
вакуума (воздуха)
-
магнитная проницаемость среды. Для
вакуума (воздуха)
 =1.
=1.
Задача 1.
Определить магнитную индукцию B поля, создаваемого отрезком бесконечно длинного прямого провода длиной l=40 см, в точке, удаленной от концов отрезка на расстояния l1=50 см и l2=30 см. Сила тока текущего по проводу, равна I=50 А.
Решение:
Согласно закону Био-Савара-Лапласа,
индукция магнитного поля
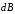 ,
создаваемого током I, протекающим
по элементу провода длиной dl в
точке, находящейся на расстоянии r
от dl, определяется выражением:
,
создаваемого током I, протекающим
по элементу провода длиной dl в
точке, находящейся на расстоянии r
от dl, определяется выражением:
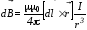 ,
,
где
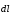 – вектор, равный по модулю длине отрезка
dl и совпадающий по направлению с
током,
– вектор, равный по модулю длине отрезка
dl и совпадающий по направлению с
током,
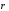 – радиус-вектор, проведенный от элемента
проводника к точке, в которой определяется
магнитная индукция, магнитная
проницаемость, магнитная
постоянная. Геометрия задачи показана
на рис. 1.
– радиус-вектор, проведенный от элемента
проводника к точке, в которой определяется
магнитная индукция, магнитная
проницаемость, магнитная
постоянная. Геометрия задачи показана
на рис. 1.
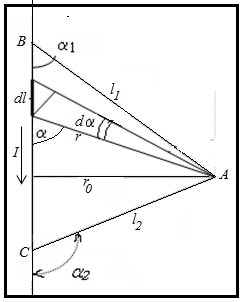
Рис.1
Для модуля вектора магнитной индукции имеем выражение
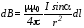 , (1)
, (1)
где - – угол между
векторами
 и
и
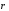 .
Из условия задачи следует, что провод
находится в немагнитной среде (в воздухе)
и, следовательно, =1.
.
Из условия задачи следует, что провод
находится в немагнитной среде (в воздухе)
и, следовательно, =1.
Пусть элемент проводника dl виден из точки А под углом d, а расстояние от точки А до провода равно r0. Из рисунка следует, что
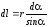 ,
,
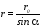 .
.
Подставляя эти выражения в формулу (1), получим:
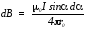 .
.
Далее необходимо использовать принцип суперпозиции, чтобы определить магнитную индукцию поля, создаваемого отрезком проводника. Для этого проинтегрируем полученное выражение по углу в пределах от до2 .
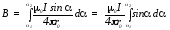 .
.
Взяв интеграл, получаем:
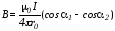 . (2)
. (2)
Из условия задачи следует, что
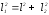 (2500=1600+900), то есть cos
r0= l2=30 см, cos
(2500=1600+900), то есть cos
r0= l2=30 см, cos
Подставляя численные значения, получим B=13,3 мкТл.
Ответ: B=13,3 мкТл
Задача 2
Найти магнитную индукцию
 на оси (в произвольной точке С)
кругового витка радиуса R
с током силой I.
Определить минимальное и максимальное
значения В.
на оси (в произвольной точке С)
кругового витка радиуса R
с током силой I.
Определить минимальное и максимальное
значения В.
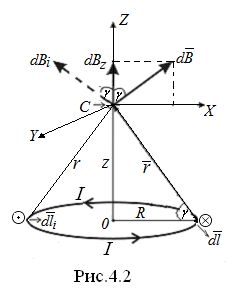
Решение:
-
Сделаем чертеж (рис. 4.2).
-
Выберем произвольный элемент длины
 кругового тока. Направление вектора
кругового тока. Направление вектора
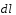 совпадает с направлением тока в месте
расположения этого элемента (на рис.4.2
направления векторов
совпадает с направлением тока в месте
расположения этого элемента (на рис.4.2
направления векторов
 и
и
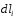 показаны как:
показаны как:
 и
и
 ).
).
Проведём
радиус-вектор
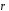 от элемента
от элемента
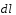 к заданной точке С.
Обозначим расстояние от С
до центра витка через z.
к заданной точке С.
Обозначим расстояние от С
до центра витка через z.
Заметим, что все элементы тока находятся от точки С на расстоянии r=const.
-
Запишем закон Био-Савара-Лапласа (4.1) для произвольного элемента
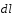 :
:
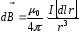 (4.8)
(4.8)
индукция
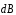 в точке С,
создана бесконечно малым элементом
тока (
в точке С,
создана бесконечно малым элементом
тока (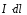 ).
).
Вектор
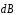 перпендикулярен плоскости, в которой
лежат соответствующие вектора
перпендикулярен плоскости, в которой
лежат соответствующие вектора
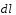 и
и
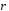 ,
и направлен в соответствии с правилом
правого винта (см. семинар №1, стр.9-10)
так, как показано на рис.4.2 – под углом
,
и направлен в соответствии с правилом
правого винта (см. семинар №1, стр.9-10)
так, как показано на рис.4.2 – под углом
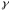 к оси Z.
к оси Z.
IV. Любой другой элемент
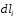 кругового тока I
создает в точке С
индукцию
кругового тока I
создает в точке С
индукцию
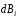 ,
направленную к оси кольца Z
также под углом
,
направленную к оси кольца Z
также под углом
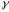 ,
причём, в заданной точке С
различные векторы
,
причём, в заданной точке С
различные векторы
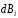 направлены не по одной прямой (их
множество образует конус с вершиной в
точке С). Так как в данном случае
реализуется ситуация, изложенная в
схеме решения на стр.74 (п.V
(б)), то необходимо ввести систему
координат XYZ
(ХY-горизонтальная
плоскость), как показано на рис. 4.2.
В силу симметрии задачи, проекции
множества векторов
направлены не по одной прямой (их
множество образует конус с вершиной в
точке С). Так как в данном случае
реализуется ситуация, изложенная в
схеме решения на стр.74 (п.V
(б)), то необходимо ввести систему
координат XYZ
(ХY-горизонтальная
плоскость), как показано на рис. 4.2.
В силу симметрии задачи, проекции
множества векторов
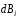 на плоскость XY
взаимно компенсируются, а проекции
(
на плоскость XY
взаимно компенсируются, а проекции
(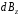 )
на ось Z
дают вклад в результирующую величину
магнитной индукции В
в точке С.
)
на ось Z
дают вклад в результирующую величину
магнитной индукции В
в точке С.
Запишем модуль вектора dB:
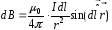 (4.9)
(4.9)
Так
как вектор
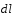 перпендикулярен вектору
перпендикулярен вектору
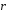 ,
то
,
то .
.
Таким образом,
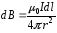 (4.10)
(4.10)
V. Проекция
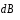 на ось Z
(рис.4.2) равна:
на ось Z
(рис.4.2) равна:
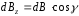 (4.11)
(4.11)
из рис.4.2 следует, что
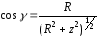 ;
и
;
и
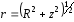
Подставив в (4.10) два последних равенства и используя выражение (4.11), получим:
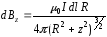
Теперь для определения модуля
результирующей магнитной индукции В
в точке С можно применить принцип
суперпозиции в виде интегрирования
последнего равенства для
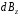 ,
вынося все константы за знак интеграла
и выбрав пределы интегрирования по l
от 0
до
,
вынося все константы за знак интеграла
и выбрав пределы интегрирования по l
от 0
до
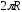 .
.
 (4.12)
(4.12)
В
соответствие с (4.12) величина
 является функцией расстояния z.
Очевидно, что минимальное значение
является функцией расстояния z.
Очевидно, что минимальное значение
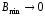 будет при
будет при
 ,
а максимальное значение
,
а максимальное значение
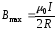 - при
- при
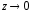 ,
то есть в центре кольца.
,
то есть в центре кольца.
Ответ: Вектор
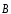 направлен вдоль оси витка, перпендикулярно
его плоскости и равен:
направлен вдоль оси витка, перпендикулярно
его плоскости и равен:
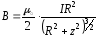
Очевидно:
 при
при
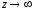 ,
,
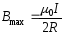 при
при
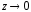 (в центре витка с током).
(в центре витка с током).
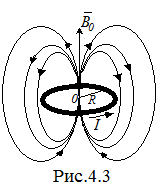
На рис. 4.3 показана пространственная
конфигурация силовых линий магнитной
индукции вокруг кольца с током ( -
магнитная индукция в центре кольца - т.
0).
-
магнитная индукция в центре кольца - т.
0).
