
1-й семестр / Лекции / Лекция 10 Исследование функции по второй производной
.docxЛекция 10

Исследование функции по второй производной
Выпуклость и вогнутость графика функции. Точки перегиба.
Рассмотрим
функция
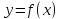 определенную, непрерывную и имеющую
непрерывные производные первого и
второго порядка в окрестности точки
определенную, непрерывную и имеющую
непрерывные производные первого и
второго порядка в окрестности точки
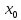 .
На графике функции возьмем точку
.
На графике функции возьмем точку
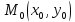 и проведем касательную к кривой в этой
точке .
и проведем касательную к кривой в этой
точке .
Определение
1.
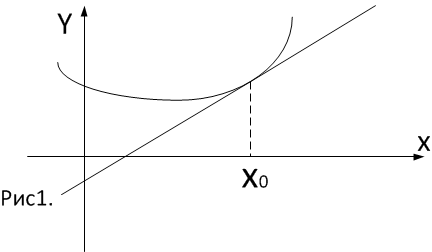
Если
в дельта окрестности точки
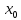 дуга кривой графика функции находится
над
касательной,
то кривая в точке
дуга кривой графика функции находится
над
касательной,
то кривая в точке
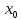 вогнута.
вогнута.
Если
в дельта окрестности точки
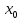 дуга кривой графика функции находится
под
касательной, то кривая в точке
дуга кривой графика функции находится
под
касательной, то кривая в точке
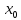 выпукла.
выпукла.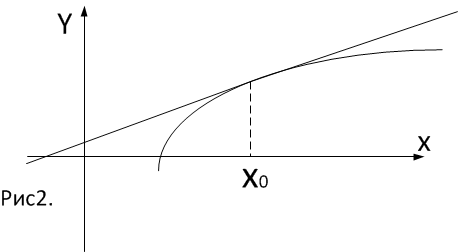
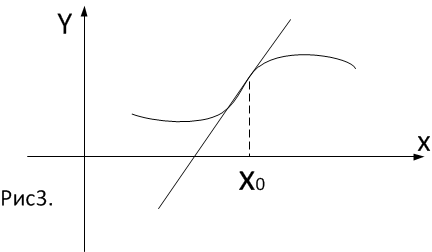
Если
в дельта окрестности точки
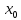 дуга кривой графика функции пересекает
касательную, то точка
дуга кривой графика функции пересекает
касательную, то точка
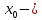 в точка
перегиба.
в точка
перегиба.
Кроме
этого, введем в рассмотрение понятие о
выпуклости и вогнутости функции на
интервале
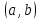 .
Пусть функция
.
Пусть функция
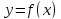 определена на интервале
определена на интервале
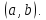
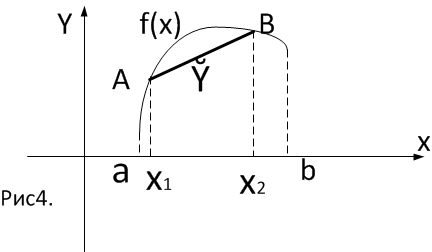
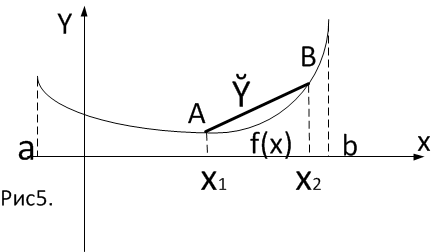
Возьмём
точки
 и через графика функции с абсциссами
и через графика функции с абсциссами
 проведем хорду AB,
ординаты которой обозначим через
проведем хорду AB,
ординаты которой обозначим через
 ,
очевидно,
,
очевидно,
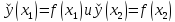 .
.
Определение 2.
Если
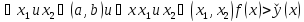 ,
то функция
,
то функция
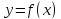 на интервале
на интервале
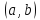 выпукла
выпукла
( выпукла вверх).
Если
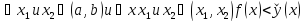 ,
то функция
,
то функция
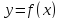 на интервале
на интервале
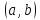 вогнута
вогнута
( выпукла вниз).
Вернемся
к рассмотрению функции
 определенной, непрерывной и имеющей
непрерывные производные первого и
второго порядка в окрестности точки
определенной, непрерывной и имеющей
непрерывные производные первого и
второго порядка в окрестности точки
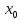 .
Геометрически ясно, что вопрос выпуклости,
вогнутости или точке перегиба зависит
от знака разности между ординатами
кривой и касательной к графику функции
в точке
.
Геометрически ясно, что вопрос выпуклости,
вогнутости или точке перегиба зависит
от знака разности между ординатами
кривой и касательной к графику функции
в точке
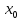 ,
т.е. от
,
т.е. от
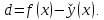
Если
в дельта окрестности точки
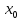
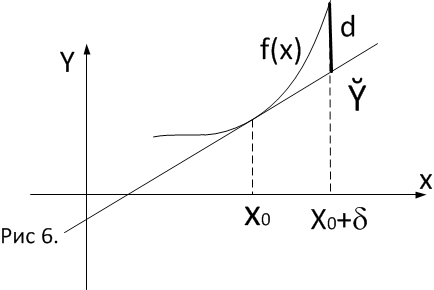
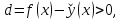
то
функция
 в точке
в точке
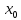 вогнута,
вогнута,
если
в
дельта окрестности точки
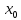
 то
функция
то
функция
 в точке
в точке
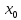 выпукла,
выпукла,
если
в
окрестности точки
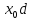 меняет знак при переходе через точку
меняет знак при переходе через точку
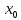 , то это точка перегиба.
, то это точка перегиба.
Теорема
1.(достаточное
условие выпуклости и вогнутости функции)
Если
функция
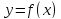 определена, непрерывна и дважды
дифференцируема на
интервале
определена, непрерывна и дважды
дифференцируема на
интервале
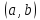 и
и
1.
 функция на
интервале
функция на
интервале
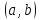 вогнута
вогнута
2.
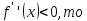 функция на
интервале
функция на
интервале
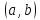 выпукла.
выпукла.
Доказательство:
Возьмём
для
 и проведем в этой точке касательную к
графику функции
и проведем в этой точке касательную к
графику функции
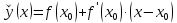
Кроме
того, в окрестности точки
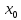 функция
функция
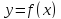 представима по формуле Тейлора (с
остаточным членом в форме Лагранжа) в
виде
представима по формуле Тейлора (с
остаточным членом в форме Лагранжа) в
виде
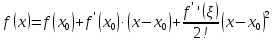
где

тогда
разность
между ординатами кривой и касательной
к графику функции в точке
 будет равна
будет равна
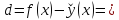

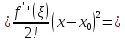
Знак
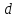 совпадает со знаком
совпадает со знаком
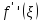 .
Для значений
.
Для значений
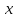 ,
близких к
,
близких к
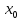 ,
в силу непрерывности функция
,
в силу непрерывности функция
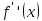 имеет тот же знак, что и
имеет тот же знак, что и
 .
.
Если
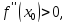 то и
то и
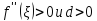 и функция в точке
и функция в точке
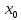 вогнута,
в силу произвольности точки
вогнута,
в силу произвольности точки
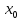 и на
интервале
и на
интервале
 .
.
Если
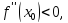 то и
то и
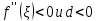 и функция в точке
и функция в точке
 выпукла,
в силу произвольности точки
выпукла,
в силу произвольности точки
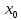 и на
интервале
и на
интервале
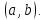

Теорема 2.(необходимое условие точки перегиба)
Если
функция
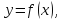 непрерывная с непрерывной производной
до второго порядка включительно, имеет
в точке
непрерывная с непрерывной производной
до второго порядка включительно, имеет
в точке
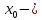 точку перегиба, то
точку перегиба, то
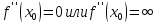
Доказательство: следует из теоремы 1.
Теорема 3.(достаточное условие точки перегиба)
Если
функция
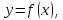 непрерывная с непрерывной производной
до второго порядка включительно, и
вторая
производная функции
непрерывная с непрерывной производной
до второго порядка включительно, и
вторая
производная функции
 при переходе через точку
при переходе через точку
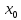 меняет знак , то точка
меняет знак , то точка
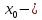 точка перегиба.
точка перегиба.
Доказательство: следует из теоремы 1.
Пример
1.
Исследовать
функцию
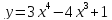
 и построить схематический график.
и построить схематический график.
1
шаг: находим
производную
функции

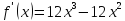
находим
стационарные точки функции
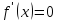
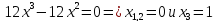
точек,
в которых
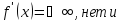 точек,
в которых производная не существует,
тоже нет.
точек,
в которых производная не существует,
тоже нет.
таким
образом, все критические точки нашей
функции
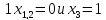
2
шаг+3 шаг: отмечаем
на оси
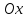 все критические
точки функции
все критические
точки функции
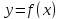 и составляем схему изменения знака
производной функции
и составляем схему изменения знака
производной функции
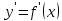 в интервалах между критическими точками
функции
+ на
основании схемы делаем вывод о интервалах
убывания или возрастания функции.
в интервалах между критическими точками
функции
+ на
основании схемы делаем вывод о интервалах
убывания или возрастания функции.
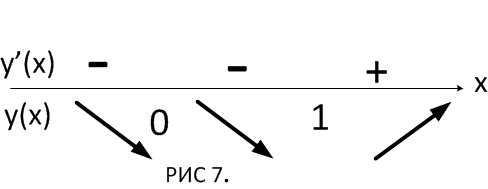
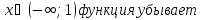
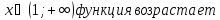
4 шаг: на основании схемы делаем вывод о характере критических точек.
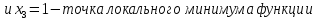
5
шаг: находим
вторую производную
функции
 и
точки, к которых вторая
производная
функции
и
точки, к которых вторая
производная
функции
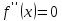 или
или
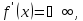 отмечаем
на оси
отмечаем
на оси
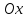 все точки
функции,
в которых
все точки
функции,
в которых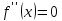 или
или
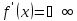 и
составляем схему изменения знака второй
производной функции
и
составляем схему изменения знака второй
производной функции
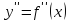 в интервалах между отмеченными точками,
на
основании схемы делаем вывод о интервалах
вогнутости или выпуклости функции.
в интервалах между отмеченными точками,
на
основании схемы делаем вывод о интервалах
вогнутости или выпуклости функции.
находим
производную
функции

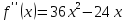
находим
точки, в которых вторая
производная
функции
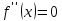

точек,
в которых
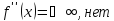
Вторая
производная функции
 меняет знак при переходе через точки
меняет знак при переходе через точки
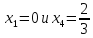 ,
,
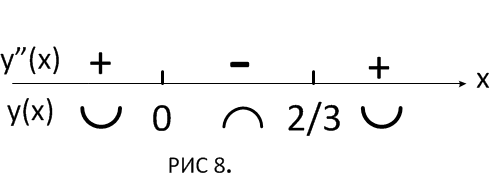
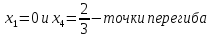
График функции имеет вид:
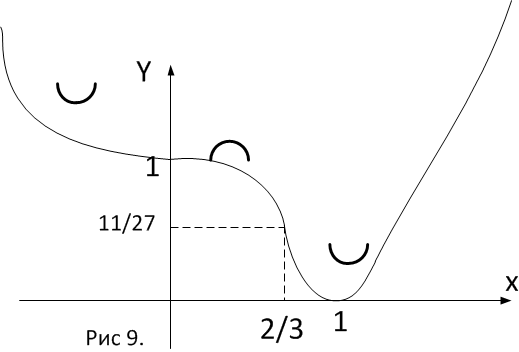
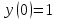
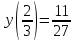
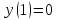
Исследование стационарных точек
с помощью производных высших порядков
Теорема 4 (достаточное условие экстремума)
Если
функция
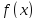 в стационарной точке x0
имеет конечную производную второго
порядка и
в стационарной точке x0
имеет конечную производную второго
порядка и
если
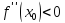 ,
то точка x0
– точка максимума функции
,
то точка x0
– точка максимума функции ,
,
если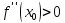 , точка x0
– точка минимума функции
, точка x0
– точка минимума функции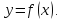
Теорема 5 (II достаточное условие точки перегиба)
Если
функция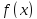 имеет в точке x0
имеет в точке x0
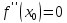 ,
,
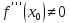 ,
то x0
– точка перегиба функции
,
то x0
– точка перегиба функции
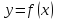 .
.
Теорема 6 (III достаточное условие экстремума)
Если
число
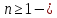 нечетно и функция
нечетно и функция
 имеет производные до
имеет производные до
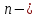 го
порядка включительно в окрестности
точки
го
порядка включительно в окрестности
точки
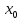 и производную
и производную
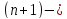 го
порядка в точке
го
порядка в точке
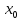 и
и
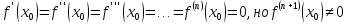 ,
то
,
то
если
 ,
то точка x0
– точка максимума функции
,
то точка x0
– точка максимума функции
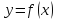 ,
,
если , точка x0
– точка минимума функции
, точка x0
– точка минимума функции
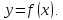
Теорема 7 (III достаточное условие точки перегиба)
Если
число
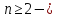 четно и функция
четно и функция
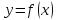 имеет производные до
имеет производные до
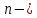 го
порядка включительно в окрестности
точки
го
порядка включительно в окрестности
точки
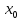 и производную
и производную
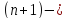 го
порядка в точке
го
порядка в точке
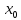 и
и
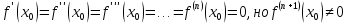 ,
то
,
то
x0
– точка перегиба графика функции
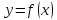 .
.
Пример
2.
Исследовать
функцию

 и построить схематический график.
и построить схематический график.
Если
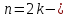 четно, то в точке
четно, то в точке
 имеем
имеем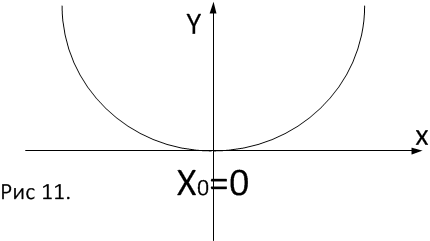
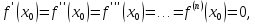
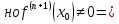
x0 – точка перегиба графика функции
Если
число
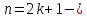 нечетно,
нечетно, 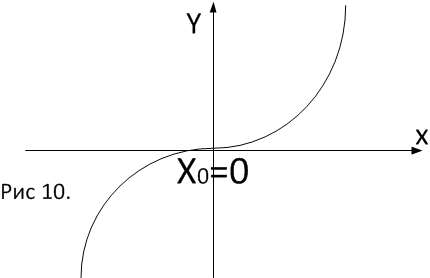
то
в точке
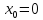 имеем
имеем

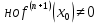
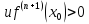 ,
,
то точка x0 – точка минимума функции

