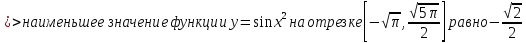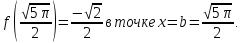1-й семестр / Лекции / Лекция 09 Исследование функции по первой производной
.docxЛекция 9

Исследование функции по первой производной
Условия постоянства, убывания и возрастания функции
Теорема
1. Если
функция
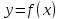 непрерывна на отрезке
непрерывна на отрезке
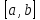 , дифференцируема на
, дифференцируема на
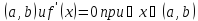 ,
то
,
то
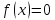 на
отрезке
на
отрезке
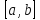 .
.
Доказательство:
Возьмём
для
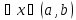 и запишем для интервала
и запишем для интервала
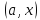 теорему Лагранжа
теорему Лагранжа
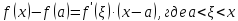
но
так как
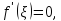 то
то
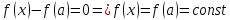 ,
,
откуда
в силу произвольности выбора точки
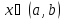 следует, что
следует, что
 постоянна на всём отрезке
постоянна на всём отрезке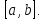

Теорема
2. Если
функция
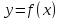 непрерывна на отрезке
непрерывна на отрезке
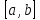 , дифференцируема на
, дифференцируема на
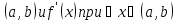 сохраняет знак, то
сохраняет знак, то
1.
если
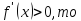 функция
функция
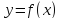 возрастает на интервале
возрастает на интервале
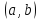
2.
если
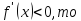 функция
функция
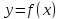 убывает на интервале
убывает на интервале
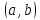
Доказательство:
Пусть
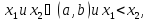 тогда по теореме Лагранжа
тогда по теореме Лагранжа
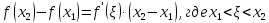
Знак
разности функций слева совпадает со
знаком производной
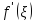 ,
откуда и следует
,
откуда и следует
1.
если
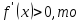
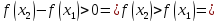
функция
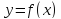 возрастает на интервале
возрастает на интервале
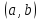
2.
если
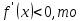
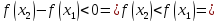
функция
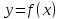 убывает на интервале
убывает на интервале
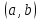

Определение 1. Точки, в которых производная функции обращается в нуль, называются стационарными точками функции.
Определение 2. Точки, в которых производная функции равна нулю, бесконечности или не существует вовсе, называются критическими точками функции.
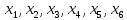 критические
точки,
критические
точки,
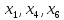 стационарные
е точки
стационарные
е точки
Локальный экстремум функции
Определение 3.
Точка
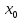 называется точкой локального максимума
функции
называется точкой локального максимума
функции
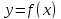 ,
если
,
если
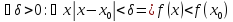 .
.
Определение 4.
Точка
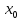 называется точкой локального минимума
функции
называется точкой локального минимума
функции
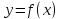 ,
если
,
если
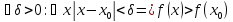 .
.
Определение
5.
Точки максимума и минимума функции
 называются точками экстремума функции.
называются точками экстремума функции.
Теорема 3.(необходимое условие экстремума функции)
Если
точка
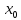 экстремум функции
экстремум функции
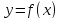
 ,
то
,
то
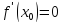 , или
, или
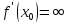 , или не существует вовсе.
, или не существует вовсе.
Другими словами, экстремум функции ищется лишь в её критических точках.
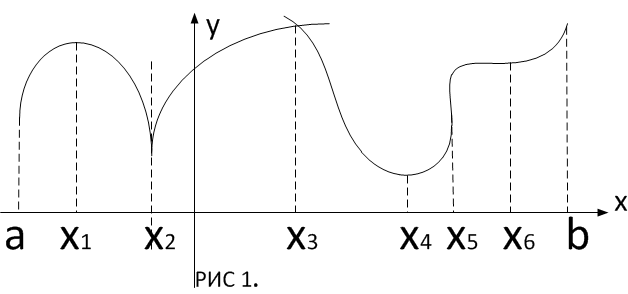
Эта
теорема, однако, не дает достаточного
условия существования экстремума. Так
на приведённом рисунке точки
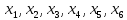 критические точки, точки
критические точки, точки
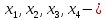 экстремум, а в точках
экстремум, а в точках
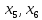 экстремума нет.
экстремума нет.
Теорема 4.(достаточное условие экстремума функции)
Если
функция
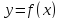 определена и дифференцируема в
окрестности точки
определена и дифференцируема в
окрестности точки
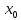 ,
где точка
,
где точка
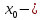 критическая точка функции, причем при
переходе через точку
критическая точка функции, причем при
переходе через точку
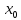 производная функции меняет знак , то
производная функции меняет знак , то
1.
если знак производной функции
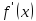 меняется с «+» на «
меняется с «+» на «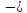 »,
то точка
»,
то точка
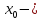 точка локального максимума функции.
точка локального максимума функции.
2.
если знак производной функции
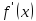 меняется
с «
меняется
с «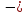 »
на «+», то точка
»
на «+», то точка
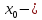 точка локального минимума функции.
точка локального минимума функции.
Доказательство:
1.
если знак меняется производной функции
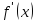 с «+» на «
с «+» на «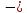 »
, то это означает, что возрастание функции
слева от точки
»
, то это означает, что возрастание функции
слева от точки
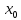 сменяется на убывание функции справа
от точки
сменяется на убывание функции справа
от точки
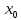 , следовательно, точка
, следовательно, точка
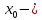 точка локального максимума функции.
точка локального максимума функции.
2.
если знак меняется производной функции
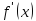 с «
с «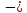 »
на «+», то это означает, что убывание
функции слева от точки
»
на «+», то это означает, что убывание
функции слева от точки
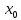 сменяется на возрастание функции справа
от точки
сменяется на возрастание функции справа
от точки
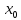 , следовательно, точка
, следовательно, точка
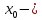 точка локального минимума функции.
точка локального минимума функции.
Замечание 1. Если при переходе через критическую точку производная не меняет знак, то в этой точке нет экстремуму функции.
Теперь можем сформулировать
Правила отыскания локального экстремума функции
(
по первой производной: ищутся экстремумы
функции
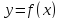
 в
конечном или бесконечном интервале и
функция
в
конечном или бесконечном интервале и
функция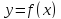
 в этом интервале предполагается
непрерывной.)
в этом интервале предполагается
непрерывной.)
1
шаг: находим
производную
функции

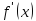
находим
стационарные точки функции
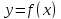 ,(
т.е. приравниваем производную к нулю и
находим корни уравнения
,(
т.е. приравниваем производную к нулю и
находим корни уравнения
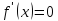
присоединяем
к найденным стационарным точкам те, в
которых
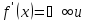
те,
к которых производная не существует,
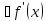
таким
образом, находим все критические точки
функции
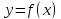
2
шаг: отмечаем
на оси
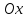 все критические
точки функции
все критические
точки функции
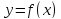 и составляем схему изменения знака
производной функции
и составляем схему изменения знака
производной функции
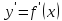 в интервалах между критическими точками
функции
в интервалах между критическими точками
функции
3 шаг: на основании схемы делаем вывод о интервалах убывания или возрастания функции.
4 шаг: на основании схемы делаем вывод о характере критических точек. Если нужно, можно построить схематический график.
Пример
1.
Исследовать
функцию
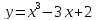
 и построить схематический график.
и построить схематический график.
1
шаг: находим
производную
функции

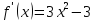
находим
стационарные точки функции
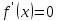
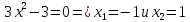
точек,
в которых
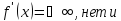 точек,
в которых производная не существует,
тоже нет.
точек,
в которых производная не существует,
тоже нет.
таким
образом, все критические точки нашей
функции
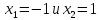
2
шаг: отмечаем
на оси
 все критические
точки функции
все критические
точки функции
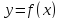 и составляем схему изменения знака
производной функции
и составляем схему изменения знака
производной функции
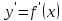 в интервалах между критическими точками
функции
в интервалах между критическими точками
функции
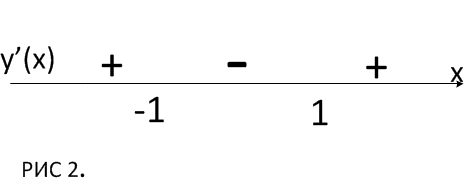
3 шаг: на основании схемы делаем вывод о интервалах убывания или возрастания функции
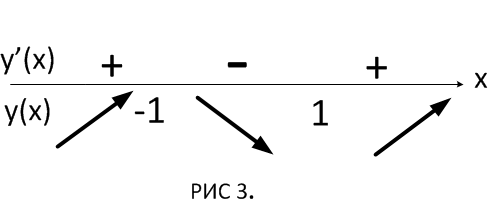
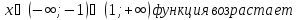
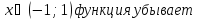
4 шаг: на основании схемы делаем вывод о характере критических точек.
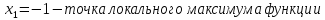
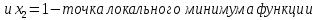
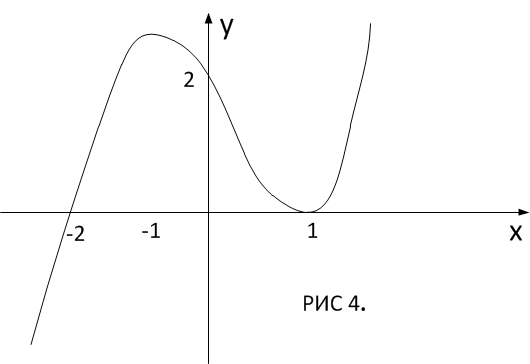
построить схематический график.
Пример
2.
Исследовать
функцию
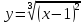
 и построить схематический график.
и построить схематический график.
1
шаг: находим
производную
функции

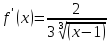
находим
стационарные точки функции
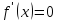
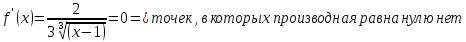
находим
точки, в которых
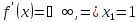
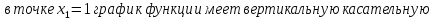
точек, в которых производная не существует, нет.
таким
образом, все критические точки нашей
функции
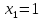
2
шаг: отмечаем
на оси
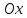 все критические
точки функции
все критические
точки функции
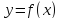 и составляем схему изменения знака
производной функции
и составляем схему изменения знака
производной функции
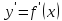 в интервалах между критическими точками
функции
в интервалах между критическими точками
функции
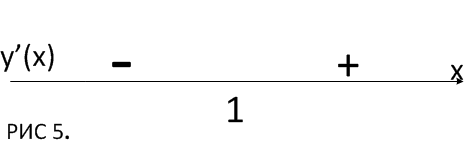
3 шаг: на основании схемы делаем вывод о интервалах убывания или возрастания функции
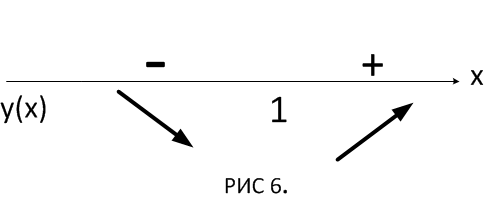
4 шаг: на основании схемы делаем вывод о характере критических точек
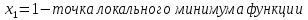
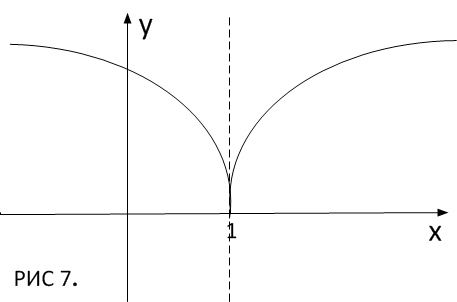
построить схематический график
Наибольшее и наименьшее значение функции на отрезке
Рассмотрим
функцию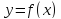
 определенную и непрерывную на отрезке
определенную и непрерывную на отрезке
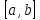 .
.
Ставится
задача: найти наибольшее и наименьшее
значение функции
 на отрезке
на отрезке
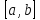 .
.
В
силу теоремы Вейерштрасса непрерывная
функция на
отрезке
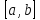 достигает в некоторой точке отрезка
своего наименьшего( и наибольшего)
значения. Рассмотрим, например, нахождение
наибольшего значения функции на отрезке
достигает в некоторой точке отрезка
своего наименьшего( и наибольшего)
значения. Рассмотрим, например, нахождение
наибольшего значения функции на отрезке
 Если наибольшее значение достигается
во внутренней точке отрезка, то это
точка одного из локальных максимумов
функции.
Если наибольшее значение достигается
во внутренней точке отрезка, то это
точка одного из локальных максимумов
функции.
Если
наибольшее значение достигается не
во внутренней точке отрезка, то это
точка одного из концов отрезка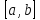 .
.
Вывод:
Для нахождения наибольшего значения
функции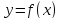
 на отрезке
на отрезке
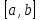 сравниваются между собой значения
функции
сравниваются между собой значения
функции
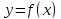 во всех точках локального максимума и
в граничных точках отрезка
во всех точках локального максимума и
в граничных точках отрезка
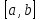 ,
выбирается наибольшее – это и есть
искомое значение.
,
выбирается наибольшее – это и есть
искомое значение.
Вывод:
Для нахождения наименьшего значения
функции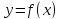
 на отрезке
на отрезке
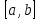 сравниваются между собой значения
функции
сравниваются между собой значения
функции
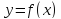 во всех точках локального минимума и в
граничных точках отрезка
во всех точках локального минимума и в
граничных точках отрезка
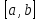 ,
выбирается наименьшее – это и есть
искомое значение.
,
выбирается наименьшее – это и есть
искомое значение.
Замечание
1.
Если сравнить значения функции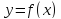 во всех
критических точках функции
во всех
критических точках функции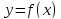
 на отрезке
на отрезке
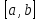 с значениями функции на концах отрезка
с значениями функции на концах отрезка
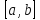 (
(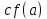 и
и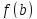 ), то наибольшее и наименьшее значения
и есть искомые величины. В этом случаи
мы избегаем дополнительного исследования
критических точек на экстремум.
), то наибольшее и наименьшее значения
и есть искомые величины. В этом случаи
мы избегаем дополнительного исследования
критических точек на экстремум.
Замечание
1.
Если
функции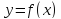 имеет
на отрезке
имеет
на отрезке
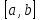 лишь одну
точку локального экстремума, то без
сравнения со значениями функции на
концах отрезка
лишь одну
точку локального экстремума, то без
сравнения со значениями функции на
концах отрезка
 (
(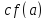 и
и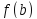 ) можно утверждать, что в этой точке
достигается наибольшее ( наименьшее)
значение функции
) можно утверждать, что в этой точке
достигается наибольшее ( наименьшее)
значение функции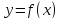 на
отрезке
на
отрезке
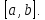
Пример
3.
Найти
наибольшее и наименьшее значение
функции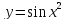
 на отрезке
на отрезке
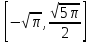 .
.
Ищем критические точки данной функции.
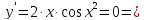
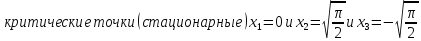
Сравниваем
значение функции во всех
критических точках функции
во всех
критических точках функции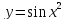
 на отрезке
на отрезке
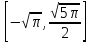 с значениями функции на концах отрезка
с значениями функции на концах отрезка
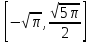 ,
имеем
,
имеем
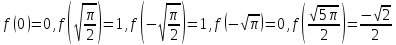
Выбираем наибольшее и наименьшее значения