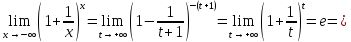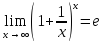1-й семестр / Лекции / Лекция 02 Предел функции
.docxЛекция 2

Предел функции
Предел функции
Зададим
некоторую функцию
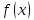 и рассмотрим поведение этой функции
при изменении
и рассмотрим поведение этой функции
при изменении
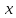 ,
в частности, при
,
в частности, при
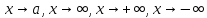 и т.д.
и т.д.
Когда
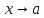 и
и
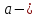 число, то будем предполагать, что функция
число, то будем предполагать, что функция
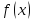 определена в окрестности точки
определена в окрестности точки
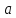 ,
за исключением, быть может, самой точки
,
за исключением, быть может, самой точки
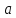 .
.
Определение
1.
Число
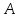 называется пределом функции
называется пределом функции
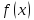 при
при
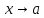 ,
если
,
если
для
любого сколь угодно малого эпсилон
больше нуля найдется дельта, функция
от эпсилон , больше нуля, такое что из
условия,
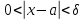 следует условие для функции
следует условие для функции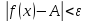
или
запишем определение на языке
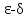
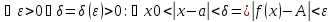
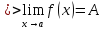
или, используя, определение окрестности точки, получим:
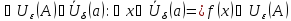
Геометрическая интерпретация :
Для
любой эпсилон окрестности предела
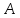 найдется дельта окрестность предельной
точки
найдется дельта окрестность предельной
точки
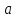 ,
такая что как только
,
такая что как только
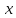 попадает в дельта окрестность предельной
точки
попадает в дельта окрестность предельной
точки
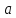 ,
так функция
,
так функция
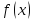 попадает в эпсилон
окрестность предела
попадает в эпсилон
окрестность предела
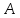 .
.
Аналогично
можно дать определение предела при
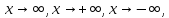 предположив, что функция
предположив, что функция
 определена при достаточно больших
значениях аргумента
определена при достаточно больших
значениях аргумента
Определение
2.
Число
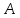 называется пределом функции
называется пределом функции
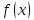 при
при
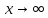 ,
если
,
если
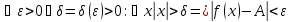
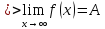
Геометрическая интерпретация :
Односторонние пределы функции
Введем
понятие одностороннего предела функции
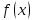 ,
предположив при этом , что функция
,
предположив при этом , что функция
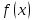 определена слева ( или справа) от точки
определена слева ( или справа) от точки
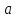 ,
то есть в интервале
,
то есть в интервале
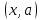 ( или в интервале
( или в интервале
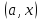 )
)
Определение
3.
Число
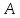 называется левосторонним пределом
функции
называется левосторонним пределом
функции
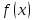 при
при
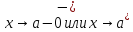 ,
если
,
если
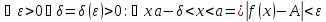
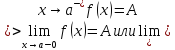
Определение
4.
Число
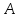 называется правосторонним пределом
функции
называется правосторонним пределом
функции
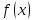 при
при
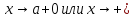 ,
если
,
если
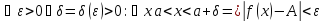
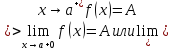
Пример1:Найти
левосторонний
и правосторонний
пределы функции
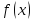
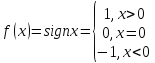
Данная
функция имеет левосторонний
при
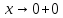 и правосторонний
при
и правосторонний
при
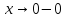 пределы,
но не имеет предела при
пределы,
но не имеет предела при
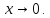
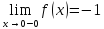
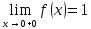
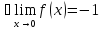
Теорема
: Если
функция
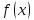 имеет в точке
имеет в точке
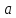 оба односторонних предела( справа и
слева) и эти пределы равны числу
оба односторонних предела( справа и
слева) и эти пределы равны числу
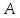 , то функция
, то функция
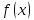 в точке
в точке
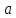 имеет предел, равный
имеет предел, равный
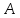 .
.
Отметим, что справедливо и обратное утверждение:
Из
существования у функции
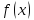 предела в точке
предела в точке
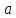 ,
равного числу
,
равного числу
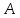 , следует существование в этой точке
обоих односторонних пределов , также
равных числу
, следует существование в этой точке
обоих односторонних пределов , также
равных числу
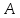 .
.
Свойства функции, имеющих предел
Теорема 1( об ограниченности функции, имеющей предел): Если
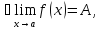
то
функция
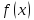 ограничена в окрестности точки
ограничена в окрестности точки
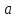 .
.
Доказательство:
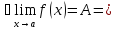
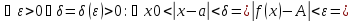
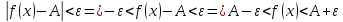
Обозначим
через
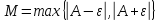 , тогда
, тогда
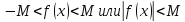
то
есть функция
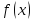 ограничена в окрестности точки
ограничена в окрестности точки
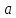 .
.
Теорема 2( о сохранении знака предела): Если
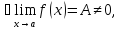
то
в некоторой окрестности предельной
точки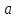 функция
функция
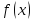 сохраняет знак предела, т.е. знак числа
сохраняет знак предела, т.е. знак числа
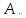
Доказательство:

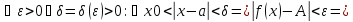
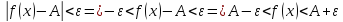
Возьмём
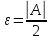 , тогда
, тогда
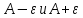 имеют знак совпадающий со знаком числа
имеют знак совпадающий со знаком числа
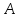
Для этого
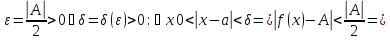
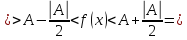
функция
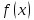 одного знака с числом
одного знака с числом
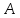 в
некоторой окрестности предельной точки
в
некоторой окрестности предельной точки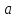 .
.
Теорема
3(
о единстве предела): Если
у функции
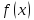
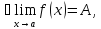
то этот предел единственный.
Доказательство(
методом от противного):
Предположим, что у функции
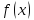 существует два предела
существует два предела
при
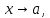 различных
между собой, т.е.
различных
между собой, т.е.

В силу определения пределов это означает, что
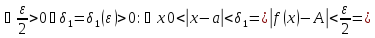
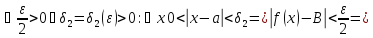
Обозначим
через
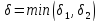 тогда при
тогда при
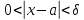 будут выполняться оба неравенства:
будут выполняться оба неравенства:
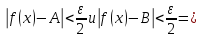
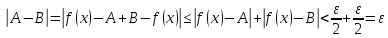
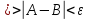
где
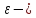 любое число, например возьмем
любое число, например возьмем
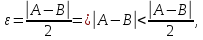
получили противоречие, значит наше предположение было не верно, а
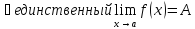
Теорема
4(
о пределе промежуточной функции): Если
в окрестности точки
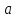
определены
три функции
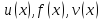 , причем выполняется соотношение
, причем выполняется соотношение
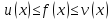 и
и
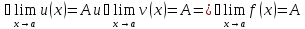
Доказательство:
из
существования пределов у функций
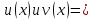
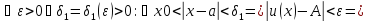
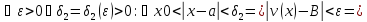
Обозначим
через
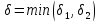 тогда при
тогда при
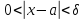 будут выполняться оба неравенства:
будут выполняться оба неравенства:
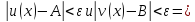
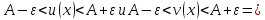
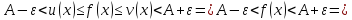
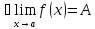
Замечательные пределы
Первый замечательный предел:
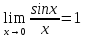
Второй замечательный предел:
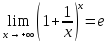
Доказательство: нам известно
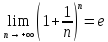
Пусть
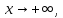
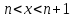 ,
где целое положительное число
,
где целое положительное число
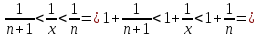
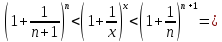
Найдем пределы последовательностей, стоящих по краям неравенства.
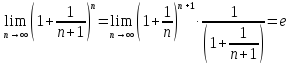
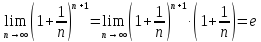
Тогда по теореме о пределе промежуточной функции
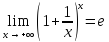
Пусть
теперь
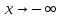 ,
введем переменную
,
введем переменную